讲授LDA基本思想，寻找最佳投影矩阵，PCA与LDA的比较，LDA的实际应用
大纲：
非线性降维算法
流形的概念
流形学习的概念
局部线性嵌入
拉普拉斯特征映射
局部保持投影
等距映射
实验环节
非线性降维算法：
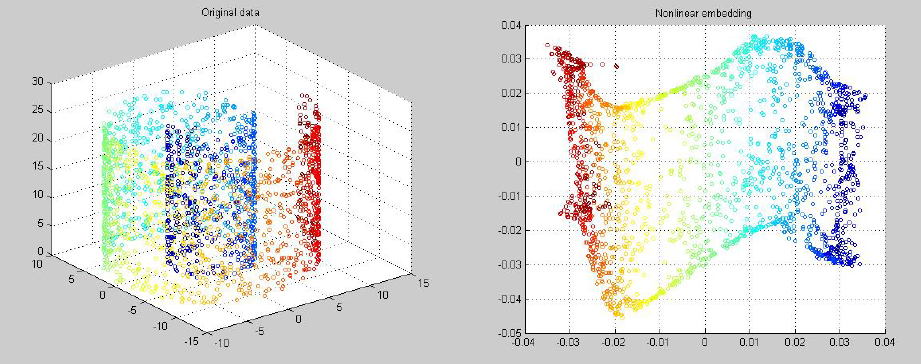
上节介绍了经典的PCA算法，它虽然在很多问题上取得了成功，但是它有它的局限性，因为在现实世界中我们要处理的很多数据它是非线性的，而PCA本身是一个线性化的算法，用线性算法处理非线性问题是不太合适的，所以我们要有非线性的降维技术。
通过一个非线性的函数将x映射到另一个空间中去，得到一个向量y，x的维度一般比y大很多。
非线性降维技术有很多经典的实现：
①核主成分分析，它用一个函数把向量映射到另外一个空间里去处理。
②神经网络，如自动编码器E，受限玻尔兹曼机RBM等。
③流行学习
流形的概念：
英文是manifold，流行是微分几何和拓扑里边的一个概念，可以认为是高维空间里的一个几何结构，如三维空间里边的一个球面，二维空间的曲线，是曲线，曲面在高维空间中的推广。
流形学习的概念：
假设数据在高维空间的分布服从某种几何形状，利用这种几何约束来完成对数据的处理，如降维，分类，聚类。
下面介绍几种经典的流行学习算法，这里是要完成数据降维任务的：
局部线性嵌入
[1] Roweis, Sam T and Saul, Lawrence K. Nonlinear dimensionality reduction by locally linear embedding. Science, 290(5500). 2000: 2323-2326.
拉普拉斯特征映射
[2] Belkin, Mikhail and Niyogi, Partha. Laplacian eigenmaps for dimensionality reduction and data representation. Neural computation. 15(6). 2003:1373-1396.
局部保持投影
[3] He Xiaofei and Niyogi, Partha. Locality preserving projections. NIPS. 2003:234-241.
等距映射
[4] Tenenbaum, Joshua B and De Silva, Vin and Langford, John C. A global geometric framework for nonlinear dimensionality reduction. Science, 290(5500). 2000: 2319-2323.
其中拉普拉斯特征映射和局部保持投影都是一种基于图论的算法。
局部线性嵌入：LLE
[1] Roweis, Sam T and Saul, Lawrence K. Nonlinear dimensionality reduction by locally linear embedding. Science, 290(5500). 2000: 2323-2326.
是整个流行学习算法的开端和鼻祖，有举足轻重的地位。
高维空间中的每个样本点可以由它周围的点近似的线性组合，用周围几个点的加权平均近似表达它，投影到低维空间里还是要保持这种局部的线性关系。
每个样本可以用它邻居的线性组合近似重构：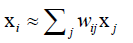
，点数是有限制的，如限定为距离它最近的k个点来表达它，这体现了局部性，同PCA一样让所有样本xi的重构误差最小化，
求解下面的最优化问题可以得到重构系数：
。第一个约束是：当xi和xj的距离||xi-xj||≤ε时它的重构权重wij非0否则为0，还有一种就是把xi最近的k个点挑出来让这些点的wij非0其他的点为0。第二个约束是权重矩阵的每一行权重系数加起来等于1。基于这些假设最终求解最优化问题得到重构洗漱wij。
得到重构系数之后，就要完成向低维空间的投影，将向量映射到低维空间，保持这种线性重构关系：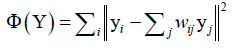
，求解该关系的最优化问题。由于局部线性嵌入会保留原始数据的拓扑结构，故降维得到的低维数据具有同高维数据一样的局部线性结构，即wij已知求低维空间的映射向量y，y还有别的约束条件，最终将y求出。
以下推理来自https://www.cnblogs.com/pinard/p/6266408.html?utm_source=itdadao&utm_medium=referral
拉普拉斯特征映射：
它是一种基于图论的方法。
用样本构造图，然后计算拉普拉斯矩阵，最后对矩阵进行特征值分解。
把样本n维空间中的点构造成一张图G，用图论中的手段解决数据降维问题。
边的权重代表相似度或距离。
图的拉普拉斯矩阵是对称半正定矩阵：
有了以上概念，就可以构造出拉普拉斯数据降维算法了。
算法流程：
①构造带权重的图
②计算图的拉普拉斯矩阵
③求解广义特征值问题，求解出特征值最大的前d个对应的特征向量，这些向量按行或按列摆开成一个矩阵（同PCA），这个矩阵就是投影矩阵，用这个矩阵左乘X，把X映射到d维空间中去。
构造带权重的图（V,E,W）：
两个点连通性判定，就是判定联通权重是否为0：1.||xi-xj||<ε，如果距离小于某个值视为联通否则不连通，2.如果是k邻近点视为联通否则非联通
权重只的计算：
求解广义特征值问题：（？不明白为什么要这样做能得到映射矩阵）
拉普拉斯特征映射核心：构造图——>计算图的拉普拉斯矩阵——>对矩阵进行特征值分解（同PCA算法一样也是求特征值问题）
局部保持投影：
它也是一种基于图论的算法，它和拉普拉斯映射相似，前面几步是一样的（构造图，计算拉普拉斯矩阵），然后它也是求解一个广义特征值问题：
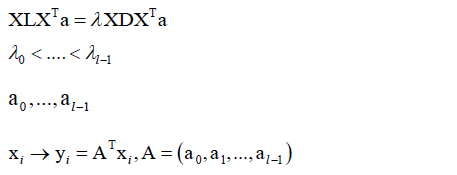
X是所有样本按照列排起来形成的矩阵，同样可证明所有特征值都大于等于零，然后得到特征值对应的特征向量，组成映射矩阵A，让A左乘向量x映射到l维空间，这和拉普拉斯映射、PCA是一样的。
等距映射：
利用微分几何里的测地线（测地线是地球表面两点之间最短弧线距离）的概念，将数据投影到低维空间之后，尽量保持原有的距离关系。
首先构造图
然后计算两点间的最短距离-Dijkstra算法：DG={dG(i,j)}，这样就可以计算流行M上任意两点之间的最短距离了dG(i,j)了。
然后求解下面的最优化问题：
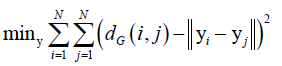，yi、yj是xi、xj投影后对应的点，投影后它们之间的距离和投影之前的距离的差异尽可能的小，即有了最优化问题，求解之后得到映射后的向量y，和局部线性嵌入有一点点像。
实验环节：
流行学习算法从2000年诞生之后，很多搞机器学习的人去搞流行学习了，数学上面看上去是非常优美的，实际应用中很少有成功的案例，美但不是很实用。
本集总结：
介绍了非线性降维的概念和主要的算法
流行、流行学习概念
四种算法：LLE、拉普拉斯特征映射、局部保持投影、等距映射
LLE主要思想是，每个样本可以由它周围的几个样本来近似的线性表达，把它投影到d维空间里之后还要这种局部线性表达的关系。拉普拉斯特征映射和局部保持投影都是一种基于图论的算法，都是对图的拉普拉斯矩阵进行广义特征值分解，得到一些特征值和特征向量，然后把最大的一些特征值和特征向量取出来，用特征向量组成投影矩阵完成投影，这和PCA有一点像。等距映射用了微分几何中测距线（非欧式空间的直线距离，而是流行上面的测地距离）的概念，把这些样本投影到d维空间里之后还要保持他们在高维空间里面的相对远近关系。
流行学习虽然数学上看起来很美，但少有成功案例。