题目:


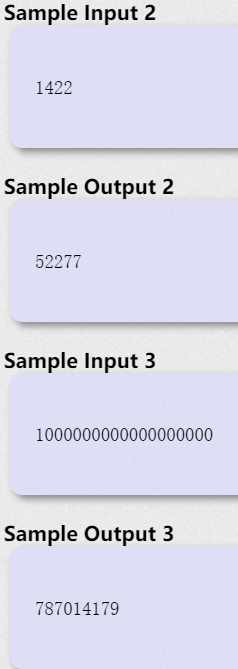
题意:
找到满足u<=n,v<=n,且存在a xor b=u,a+b=v,的数对(u,v)的个数。
分析:
n很大,挨个递推就不太好了,不过我们先想一想可以怎么稍微暴力点的递推:fi=fi-1+Coi,也就是一个一个来,Coi表示和为i的有多少个异或之后有多少结果。当然,这样复杂度是无法接受的。数组开不下,来个递归处理,当然函数也占地方。
都想到递归了,想一想有什么别的递归方式,有的,fi=f(i/2)+f((i-1)/2)+f((i-2)/2)(除法向下取整),为什么呢?首先先证明下界,即fi>=f(i/2)+f((i-1)/2)+f((i-2)/2)(除法向下取整),我们尝试构造,我们给得到i/2以内的数对x1,y1的数字a1,b1,最后一位(二进制为)补一个0,新的到的数字a,b,那么有,a+b<=n,a xor b<=n,且不会重复,我们给得到(i-1)/2以内的数对的数字补1和0,同样可以得到新的数字和数对,且不重,同样,给(i-2)/2以内的补两个1,同样不重,且三组里的数对没有重复。为什么呢?首先末尾补0,1的一定和另两个组不同,而补0,0和补1,1的异或如果想等,那么倒数第二位的和相等,但是由于1,1进位,所以和的倒数第二位将不会想等,于是有fi>=f(i/2)+f((i-1)/2)+f((i-2)/2)(除法向下取整),然后证明上界,即fi<=f(i/2)+f((i-1)/2)+f((i-2)/2)(除法向下取整),类似的方法,给这些数字最后一位抹掉,发现新的数对数量不会超过f(i/2)+f((i-1)/2)+f((i-2)/2)(除法向下取整)。于是我们有了fi<=f(i/2)+f((i-1)/2)+f((i-2)/2)(除法向下取整),于是有fi=f(i/2)+f((i-1)/2)+f((i-2)/2)(除法向下取整),当然,为了快一点,我们会合并一下(分奇偶),然后没次递归就只调用两个函数(其实调用3个也差不多,因为将会有两个一样),然后再记忆化一下。
最后复杂度的证明:需要处理出的数最多有:x,x/2,x/2-1,x/4,x/4-1,x/4-2,x/8,x/8-1,x/8-2,x/8-3,所以复杂度应该是(logn)的平方,然后就是代码。
#include <cstdio> #include <map> const int mod=1e9+7; using namespace std; map<long long,int> ma; int Cl(long long x){ if(ma[x]) return ma[x]; if(x&1) return ma[x]=((long long)Cl(x/2ll)*2ll+Cl(x/2ll-1ll))%mod; return (Cl(x/2ll-1ll)*2ll+Cl(x/2ll))%mod; } int main(){ long long n; scanf("%lld",&n); ma[0]=1; ma[1]=2; ma[2]=4; ma[3]=5; ma[4]=8; printf("%d",Cl(n)); return 0; }