给出一张图,求出图上某一个节点到其他节点的最短路径,这就是单源最短路径问题。
单源最短路径问题应该是图论中最著名的问题之一了,也是众多图论新手最先学习的算法。最短路问题也有各种变体,简单的可以是 floyd 的裸橙题,难的可以结合其他算法和数据结构达到黑题难度。总之,单源最短路径问题是图论中非学不可的算法!
在这里,我会详解三种常见的算法:Floyd 算法,SPFA 算法(虽然已死)和 Dijkstra 算法,对应的思路分别是动态规划,搜索和贪心。面对不同的问题,三种算法各有自己的优势。
目录
-
例题
-
Floyd 算法简述
-
Floyd 算法优化
-
SPFA 算法详解
-
SPFA 算法代码
-
Dijkstra 算法详解
-
Dijkstra 算法代码
-
Dijkstra 的堆优化
-
Dijkstra 为什么不能处理负边权
例题
题目背景
本题测试数据为随机数据,在考试中可能会出现构造数据让 SPFA 不通过,如有需要请移步 P4779。
题目描述
如题,给出一个有向图,请输出从某一点出发到所有点的最短路径长度。
输入格式
第一行包含三个整数 (n,m,s),分别表示点的个数、有向边的个数、出发点的编号。
接下来 (m) 行每行包含三个整数 (u,v,w) 表示一条 (u o v) 的,长度为 (w) 的边。
输出格式
输出一行 (n) 个整数,第 (i) 个表示 (s) 到第 (i) 个点的最短路径,若不能到达则输出 (2^{31}-1)。
Floyd 算法
Floyd 算法是一种动态规划算法,时间复杂度为 (Theta(n^3)),其中 (n) 为节点数量。该方法简单易懂,也是一般大家最先接触的算法。
该方法一般用于处理小数据,所以一般搭配邻接矩阵使用。代码也应该是三种方法中最短的。但是 Floyd 考场慎用,因为它跑得太慢了!
Floyd 算法的思路是枚举 (i,j,k),判断 (i o j) 的路径经过 (k) 是否更短,如果更短,就更新答案。在执行完操作后,矩阵中的 (f_{i,j}) 即为点 (i) 到 (j) 的最短路径。
注意开始时要将矩阵初始化为一个很大的数,比如 0x7fffffff。
输出时也要注意,要在 (f_{s,s}) 时输出零。
#include<bits/stdc++.h>
using namespace std;
#define rg register
#define inf 0x7fffffff
long long n,m,s,u,v,w;
long long f[1005][1005];
int main()
{
cin>>n>>m>>s;
for(rg int i=1;i<=n;++i)
for(rg int j=1;j<=n;++j)
f[i][j]=inf; //初始化。
for(rg int i=0;i<m;++i)
{
cin>>u>>v>>w;
f[u][v]=min(f[u][v],w); //取 min 可以应对重边。
} //因为不取 min 的话,后输入的一条重边比先输入的长,就会记录错误的答案。
for(rg int k=1;k<=n;++k)
for(rg int i=1;i<=n;++i)
for(rg int j=1;j<=n;++j)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]); //判断经过 k 的路径是否更短。
f[s][s]=0; //这里一定要为 0,不然输出时就会 0x7fffffff。
for(rg int i=1;i<=n;++i)
cout<<f[s][i]<<" ";
return 0;
}
Floyd 的优化
经过观察,我们发现,当 (i=k) 时,就会变成 (i o j) 的路径是否经过 (i),十分可笑和浪费时间,在这里我们就可以跳。如果 (f_{i,k}) 为 0x7fffffff 时,就代表两点间不存在路径,我们也可以跳过。
同理,对于 (j) 和 (k) 我们也可以这么做,但是在第三重循环中 continue 基本没有意义,所以我们可做可不做。
优化过的代码:
#include<bits/stdc++.h>
using namespace std;
#define rg register
#define inf 0x7fffffff
long long n,m,s,u,v,w;
long long f[1005][1005];
int main()
{
cin>>n>>m>>s;
for(rg int i=1;i<=n;++i)
for(rg int j=1;j<=n;++j)
f[i][j]=inf; //初始化。
for(rg int i=0;i<m;++i)
{
cin>>u>>v>>w;
f[u][v]=min(f[u][v],w); //取 min 可以应对重边。
} //因为不取 min 的话,后输入的一条重边比先输入的长,就会记录错误的答案。
for(rg int k=1;k<=n;++k)
for(rg int i=1;i<=n;++i)
{
if(i==k||f[i][k]==inf) //判断。
continue;
for(rg int j=1;j<=n;++j)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]); //判断经过 k 的路径是否更短。
}
f[s][s]=0; //这里一定要为 0,不然输出时就会 0x7fffffff。
for(rg int i=1;i<=n;++i)
cout<<f[s][i]<<" ";
return 0;
}
SPFA
虽然说 SPFA 已死,但是处理负边权时还是要用 SPFA,dijktra 的贪心在负边权时会出错(为什么会出错会在后面讲),所以 SPFA 还是要掌握的。
其实 SPFA 就是一种搜索。常见的 SPFA 都是用 bfs,(但 也有用 dfs 实现的)。它与普通的 bfs 求不带权的最短路区别是:普通 bfs 在搜到目标节点后就会立即终止循环,并标记这个节点已经访问过,就不会第二次搜索;但是 SPFA 中一个节点可能会反复入队好几次。
SPFA 的思想是从起始节点开始,将与当前节点有边直接相连的节点入队,不断向外拓展,记录路径长度,当有一条从起始节点到 (i) 节点的路径比先前求出的更短,就更新答案,并将 (i) 节点入队。然后取出队列的下一个节点,弹出 (ldotsldots) 反复进行这种操作,直到队列为空,此时就是最短路径了。
结合图一步步模拟:
样例中的图是这样的:
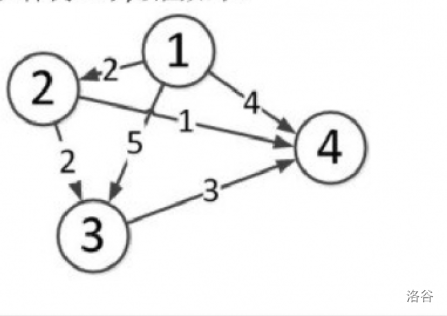
我们将答案数组 (dis) 初始化(此时队列有 1):

从节点 1 开始遍历,将与 1 相连的节点松弛、入队(此时队列有 2、3、4):

然后将 1 弹出,对 4 进行操作,发现没有 4 能到达的节点,不作改变(此时队列中有 3、2):

将 4 弹出,对 3 进行操作,3 与 4 相连,但是 (1 o 3 o 4) 的权值大于 (dis[4]),所以仍然不进行操作(此时队列中有 2):

将 3 弹出,对 2 进行操作,与 2 相连的节点松弛(此时队列中有 3、4):

分别对 3、4 操作,发现得不到最短路径,先后弹出 3、4(此时队列为空):

队列为空,跳出循环,(dis) 即为最短路径。
代码实现(链式前向星):
#include<bits/stdc++.h>
using namespace std;
#define rg register
#define inf 0x7fffffff
struct node
{
int ne,to,val; //前向星存储。
};
vector<node> a; //vector 实现链表。
queue<int> q;
int n,m,s,u,v,w,cnt;
long long dis[1005],vis[1005],head[1005]; //dis 是答案,vis 记录节点是否在队列中。
// head 是前向星用的,记录节点引出的最后一条边。
inline void add(int u,int v,int w) //建立一条边。
{
node now;
now.ne=head[u];
now.to=v;
now.val=w;
head[u]=++cnt;
a.push_back(now);
}
inline void SPFA()
{
q.push(s);
dis[s]=0;
vis[s]=1;
while(q.empty()==0)
{
int now=q.front();
q.pop();
vis[now]==0;
for(rg int i=head[now];i;i=a[i].ne) //前向星遍历图的方式。
{ //通过 head 节点逐一找到与 now 相连的边。
int to1=a[i].to;
if(dis[to1]>dis[now]+a[i].val) //如果通过 now 到达 to1 的路径更短,更新答案。
{
dis[to1]=dis[now]+a[i].val;
if(vis[to1]==0) //如果不在队列中,就入队。
{
vis[to1]=1;
q.push(to1);
}
}
}
}
}
int main()
{
cin>>n>>m>>s;
for(rg int i=1;i<=n;++i)
dis[i]=inf; //初始化 dis。
a.push_back((node){0,0,0}); //为了方便,a[0] 我们不用,从 a[1] 开始。
for(rg int i=0;i<m;++i)
{
cin>>u>>v>>w;
add(u,v,w);
//add(v,u,w) 如果无向图要建两条。
}
SPFA();
for(rg int i=1;i<=n;++i) //输出。
cout<<dis[i]<<" ";
return 0;
}
Dijkstra
Dijkstra 是一种贪心的思想,在解决不含负边权的图的最短路中是最优秀的做法。未优化的时间复杂度为:(Theta(n^2))。
Dijkstra 的思想是每次找到一个节点 (i),要求从初始节点到 (i) 的路径权值和最小,且该节点是第一次成为这样的节点。然后将其他和此节点相连的节点松弛操作。当 (n) 个节点全部都作为过这样的点,那么 (dis) 数组就是最优解了。
算法详解:
首先还是以样例为例:

初始化,除 (dis[1]) 为 (0),其他 (dis) 全为 inf,图中的节点都未访问过(蓝点):

此时找到起始点 1,将与其相连的点松弛((dis[2]=2),(dis[3]=5),(dis[4]=4)):

然后找到 (dis) 值最小的蓝点 2,标白,将与其相连的点松弛((dis[3]=4),(dis[4]=3)):
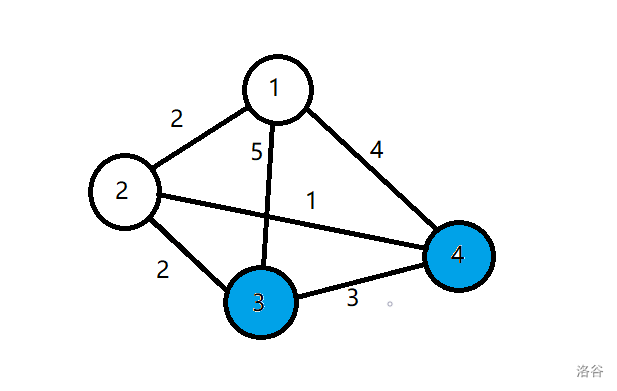
再找到 (dis) 值最小的蓝点 4,标白,发现从 4 到达不了其他点,跳过:
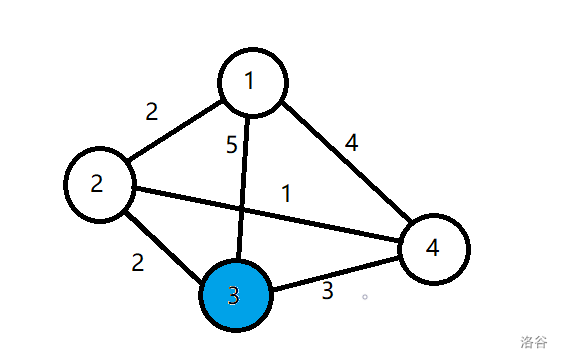
最后找到最后一个蓝点 3,发现没有点能松弛,因为已经是最短路径了,把 3 标白,此时图中没有蓝点,结束 Dijkstra。

代码:
#include<bits/stdc++.h>
using namespace std;
#define rg register
#define inf 0x7fffffff
struct node
{
int ne,to,val; //前向星存储。
};
vector<node> a; //vector 实现链表。
int n,m,s,u,v,w,cnt,mi,mn; //mi 是当前 dis 最小的蓝点编号,mn 是该点的 dis 值。
long long dis[1005],vis[1005],head[1005]; //dis 是答案,vis 记录节点是否在队列中。
// head 是前向星用的,记录节点引出的最后一条边。
inline void add(int u,int v,int w) //建立一条边。
{
node now;
now.ne=head[u];
now.to=v;
now.val=w;
head[u]=++cnt;
a.push_back(now);
}
inline void dijktra()
{
mi=s;
dis[s]=0;
for(rg int i=1;i<=n;i++) //第一重循环,遍历图。
{
if(i!=1) //注意在起始点时要特判。
{
mn=inf;
for(rg int i=1;i<=n;++i)
{
if(vis[i]==0&&dis[i]<mn)
mn=dis[i],mi=i; //找到最小蓝点。
}
}
vis[mi]=1;
for(rg int i=head[mi];i;i=a[i].ne) //松弛与其相连的点。
{
if(dis[a[i].to]>dis[mi]+a[i].val)
dis[a[i].to]=dis[mi]+a[i].val;
}
}
}
int main()
{
cin>>n>>m>>s;
for(rg int i=1;i<=n;++i)
dis[i]=inf; //初始化 dis。
a.push_back((node){0,0,0}); //为了方便,a[0] 我们不用,从 a[1] 开始。
for(rg int i=0;i<m;++i)
{
cin>>u>>v>>w;
add(u,v,w);
//add(v,u,w) 如果无向图要建两条。
}
dijktra();
for(rg int i=1;i<=n;++i) //输出。
cout<<dis[i]<<" ";
return 0;
}
Dijkstra 的堆优化
我们知道,有一直神奇的数据结构,叫做堆。它可以用 (Theta(log_2n)) 的时间复杂度维护,堆顶就是最小(大)的元素。
因此,在找最小节点的时候,我们可以用堆来实现,让 Dijkstra 跑得更快。
在这里,我懒得手打堆,就用 STL 中的容器 priority_queue(优先队列) 来作示范:
代码:
#include<bits/stdc++.h>
using namespace std;
#define rg register
#define inf 0x7fffffff
struct node
{
int ne,to,val; //前向星存储。
};
struct minb
{
int mi,mn;
bool operator <(const minb &x)const //这里是优先队列比较时要用的重载运算符。
{
return x.mn<mn;
}
};
vector<node> a; //vector 实现链表。
priority_queue<minb> q;
int n,m,s,u,v,w,cnt;
long long dis[1005],vis[1005],head[1005]; //dis 是答案,vis 记录节点是否在队列中。
// head 是前向星用的,记录节点引出的最后一条边。
inline void add(int u,int v,int w) //建立一条边。
{
node now;
now.ne=head[u];
now.to=v;
now.val=w;
head[u]=++cnt;
a.push_back(now);
}
inline void dijktra()
{
dis[s]=0;
q.push((minb){s,0});
while(q.empty()==0) //队列非空。
{
minb x=q.top(); //取出最小蓝点。
q.pop();
if(vis[x.mi]) //如果不是蓝点,跳出。
continue;
vis[x.mi]=1;
for(rg int i=head[x.mi];i;i=a[i].ne)
{
if(dis[a[i].to]>dis[x.mi]+a[i].val)
{
dis[a[i].to]=dis[x.mi]+a[i].val;
if(vis[a[i].to]==0) //如果此点为蓝点,就可以入队。
q.push((minb){a[i].to,dis[a[i].to]});
}
}
}
}
int main()
{
cin>>n>>m>>s;
for(rg int i=1;i<=n;++i)
dis[i]=inf; //初始化 dis。
a.push_back((node){0,0,0}); //为了方便,a[0] 我们不用,从 a[1] 开始。
for(rg int i=0;i<m;++i)
{
cin>>u>>v>>w;
add(u,v,w);
//add(v,u,w) 如果无向图要建两条。
}
dijktra();
for(rg int i=1;i<=n;++i) //输出。
cout<<dis[i]<<" ";
return 0;
}
Dijkstra 为什么处理不了负边权
其实 Dijkstra 贪心策略的正确是建立在一个 xxs 都能推出来的一个定理:如果 (a<b),(cgeq 0),则 (a<b+c)。
在这里,(a) 就相当于 (dis) 值最小的蓝点的 (dis) 值,(b) 代表其他任意点的 (dis) 值,(c) 为连接 (a)、(b) 两点路径的 (dis) 值。
在边权不为负时,(dis) 值也不为负,既然 (a) 的 (dis) 已经最小了,那么从 (b) 到 (c) 绕一个弯子再到 (a) 肯定比直接到 (a) 的路径长。
但是引入负边之后,就不一样了,这时的贪心所得的的局部最优解就不一定是全局最优解了,Dijkstra 也失去了效力。
小结
不同的方法对付不同的问题。本篇文章讲的是最短路问题中的最基础的东西,由这些基础能拓宽到其他的难题,碰到那些题时,就不能死套模板,要灵活运用。