http://codeforces.com/contest/1091/problem/D
题目大意:
n个数的全排列按顺序写出来,求为连续n个数且和为n(n+1)/2的子串个数
思路:
对于分别在两个排列中的连续n个数
设其前a个数为前一个排列的末尾a个数,s,后(n-a)个数为后一个排列的开头(n-a)个数
需要满足这两组数无交集
又因为排列按字典序,后一个排列为前一个排列字典序+1
若s1单调递减,则可证明字典序+1后必出现新的数在排列的后a个数中,不合题意
否则这个排列ok
ans=n*n!-c(n,k)*(n-k)!

#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; const int MOD=998244353,maxn=1e6+4; int n; long long inv[maxn],jc[maxn]; inline long long power(long long a,int b){ long long r=1; while(b){ if(b&1) r=(r*a)%MOD; a=(a*a)%MOD; b>>=1; } return r; } long long c(int a,int b){ long long h=power((jc[b]*jc[a-b])%MOD,MOD-2); h=(h*jc[a])%MOD; return h; } int main(){ cin>>n; jc[1]=1;jc[0]=1; for(int i=1;i<=n;i++) jc[i]=(jc[i-1]*i)%MOD; long long ans=jc[n]*n%MOD; for(int i=1;i<n;i++){ long long h=(jc[n-i]*c(n,i))%MOD; ans=((ans-h)%MOD+MOD)%MOD; } cout<<ans; }
http://codeforces.com/contest/1091/problem/F
题目大意:
G W L
草 水 岩
走 游 飞
飞 飞
走 5s 游 3s 飞 1s
energy=0
走、游一个单位长度距离,energy+1
飞一个单位长度距离,energy-1
任意时刻energy>=0
求最短时间
思路:
由于L必须飞,首先求出在G、W上多走、游的距离,G一直向后修改到W,前缀和算
eg:GLGLGLGWLGLLLGW
修改第一个G和第一个W
可证不会为了WG省时间而多飞
多余的时间用在GW上
用在G更优
用在靠后的G更优
写了1h,拍了1h,WA了8次……

#include<iostream> #include<cstdio> #include<algorithm> using namespace std; inline long long read() { long long x=0, w=1; char ch=getchar(); while (ch<'0' || ch>'9') { if (ch=='-') w=-1; ch=getchar(); } while (ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0', ch=getchar(); return x*w; } const int maxn=1e5+4; int n; long long l[maxn],sum[maxn]; char c[maxn]; int main(){ scanf("%d",&n); for(int i=1;i<=n;i++) l[i]=read(); scanf("%s",c+1); if(c[1]=='L'){ cout<<0; return 0; } int t=0;char ch=' '; long long num=0,p=0; for(int i=1;i<=n;i++){//要多走的路,这块子p和num怎么改,什么时候改卡了我好久 if(!t&&c[i]!='L') {t=i;ch=c[i];} if(c[t]=='G'&&c[i]=='W'){ if(p>0) {l[t]+=p;num-=p;p=0;} t=i; } if(c[i]=='L') num+=l[i]; else num-=l[i]; p=max(p,num); } if(p>0) l[t]+=p; long long ans=0; sum[0]=0; for(int i=1;i<=n;i++){//多余的能量先不用得到的ans if(c[i]=='L') {ans+=l[i];sum[i]=sum[i-1]-l[i];} else { sum[i]=sum[i-1]+l[i]; if(c[i]=='G') ans+=(long long)5*l[i]; else ans+=(long long)3*l[i]; } } long long m=0x7fffffffffffffff; for(int i=n;i;i--){//多余的能量用来走G m=min(m,sum[i]); if(m<=0) break; if(m>0&&c[i]=='G'){ if(m>=2*l[i]) {m-=(long long)2*l[i];ans-=(long long)4*l[i];l[i]=-l[i];} else {l[i]-=m;ans-=(long long)2*m;m=0;break;} } } sum[0]=0; for(int i=1;i<=n;i++){ if(c[i]=='L') sum[i]=sum[i-1]-l[i]; else sum[i]=sum[i-1]+l[i]; } m=0x7fffffffffffffff; for(int i=n;i;i--){//多余的能量用来走W m=min(m,sum[i]); if(m<=0) break; if(m>0&&c[i]=='W'){ if(m>=2*l[i]) {m-=(long long)2*l[i];ans-=(long long)2*l[i];l[i]=-l[i];} else {l[i]-=m;ans-=m;m=0;break;} } } cout<<ans; }
取金币1
取金币2
取金币k (https://www.luogu.org/problemnew/show/P2045)
斗地主 (http://uoj.ac/problem/160)
题目大意:
这是一道提交答案题。
A与B玩双人斗地主,规则就是斗地主规则,A先出牌。
假设双方都足够聪明,若最终A能赢,求B至多有几张牌剩余,若最终B能赢,求A至少有几张牌剩余。
假设初始时A的牌数为x,B的牌数为y。
对于20%的数据x=3,y=8。
对于20%的数据x=4,y=10。
对于20%的数据x=5,y=12。
对于20%的数据x=5,y=16。
对于20%的数据x=5,y=20。
对于100%的数据,T=2000且数据近似随机。按提交的输出中正确的行数给分。
思路:
f(a,b,0/1,c) {auto x: max(f(?,?,?,?)); } 2^5 * 2^20 * 100 * 100
a,b为当前A,B手中牌的状态,0/1为当前轮到谁打了,c为上一轮打的状态
考虑搜索所需参数
当前A的手牌状态,当前B的手牌状态,上一轮对方出的牌,当前是谁出牌。
直接记忆化搜索。
经典题+ http://hihocoder.com/problemset/problem/1580
题目大意:
有一个n*m的矩阵,可以将其中一个数改为p,要求使得最大子矩阵最大。
n,m<=300。
思路:
O(n^2)枚举行数上下界i,j,s[k]=sigma a[h][k](h=i->j)
若不考虑换点,显然对s[k]直接dp
由于考虑换点,故在dp上加一维0/1表示是否已换过点,进行状态转移
代码:容易写挂,注意细节

#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; inline int read() { int x=0, w=1; char ch=getchar(); while (ch<'0' || ch>'9') { if (ch=='-') w=-1; ch=getchar(); } while (ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0', ch=getchar(); return x*w; } int n,m,p; int a[304][304],s[304],minn[304],dp[304][2],ans=0; int main(){ int sum; while(scanf("%d%d%d",&n,&m,&p)!=EOF){ ans=-1000000000;sum=0; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){ a[i][j]=read(); sum+=a[i][j]; } for(int i=1;i<=n;i++){ memset(s,0,sizeof(s)); memset(minn,0x3f,sizeof(minn)); for(int j=i;j<=n;j++){ memset(dp,0xc0,sizeof(dp)); dp[0][0]=0; for(int k=1;k<=m;k++) { s[k]=s[k]+a[j][k]; minn[k]=min(minn[k],a[j][k]); dp[k][0]=max(s[k],s[k]+dp[k-1][0]); dp[k][1]=max(max(0,dp[k-1][0])+p-minn[k]+s[k],dp[k-1][1]+s[k]); ans=max(ans,dp[k][1]); if(i!=1||j!=n||k!=m||dp[k][0]!=sum) ans=max(ans,dp[k][0]); } } } printf("%d ",ans); } return 0; }
经典题++ http://hihocoder.com/problemset/problem/1634
题目大意:
有一个n*m的矩阵,可以将其中一个数改为p,要求使得最大子矩阵最小。
n,m<=300。
思路:
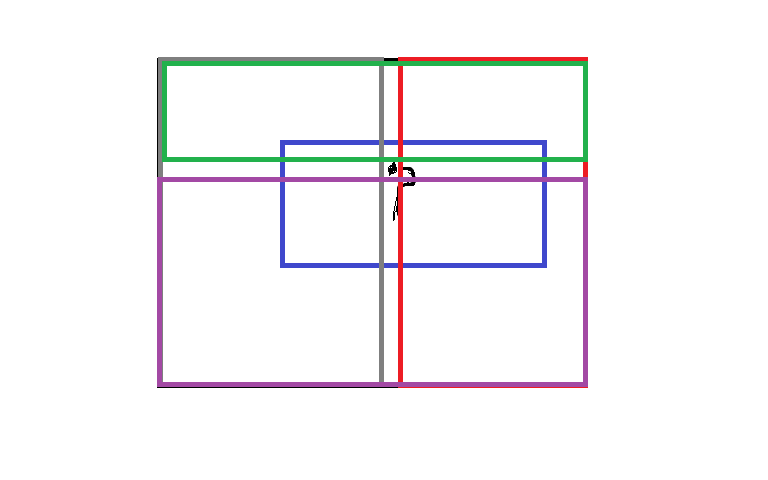
先求得原矩阵最大子矩阵,O(N^2)枚举换成p的点,则对答案有影响的要么是最大子矩阵换成p以后的值,要么另外的未经修改的原矩阵的子矩阵,显然它不经过修改的点,所以单独存在于如图所示四个长方形中
ans=min{max{最大子矩阵把k换成p,四个矩形最大子矩阵最大值}}

#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; inline int read() { int x=0, w=1; char ch=getchar(); while (ch<'0' || ch>'9') { if (ch=='-') w=-1; ch=getchar(); } while (ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0', ch=getchar(); return x*w; } int n,m,p,num; int a[304][304],s[304],dp[304],zy[304],ans=0,l1,r1,l2,r2,sum1[154],sum2[154],sum3[154],sum4[154]; int main(){ while(scanf("%d%d%d",&n,&m,&p)!=EOF){ memset(sum1,0xc0,sizeof(sum1)); memset(sum2,0xc0,sizeof(sum2)); memset(sum3,0xc0,sizeof(sum3)); memset(sum4,0xc0,sizeof(sum4)); num=-1000000000;ans=1000000000; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){ a[i][j]=read(); } for(int i=1;i<=n;i++){ memset(s,0,sizeof(s)); for(int j=i;j<=n;j++){ memset(dp,0xc0,sizeof(dp)); dp[0]=0; for(int k=1;k<=m;k++) { s[k]=s[k]+a[j][k]; if(dp[k-1]>=0&&k!=1){ zy[k]=zy[k-1]; dp[k]=dp[k-1]+s[k]; }else{ zy[k]=k; dp[k]=s[k]; } if(num<dp[k]){ l1=i,r1=j,l2=zy[k],r2=k; num=dp[k]; } sum1[j]=max(sum1[j],dp[k]); sum3[k]=max(sum3[k],dp[k]); } } } for(int i=1;i<=n;i++){ memset(s,0,sizeof(s)); for(int j=i;j<=n;j++){ memset(dp,0xc0,sizeof(dp)); dp[0]=0; for(int k=m;k;k--) { s[k]=s[k]+a[j][k]; if(dp[k+1]>=0&&k!=m){ dp[k]=dp[k+1]+s[k]; }else{ dp[k]=s[k]; } sum4[k]=max(sum4[k],dp[k]); } } } for(int i=1;i<=n;i++){ memset(s,0,sizeof(s)); for(int j=i;j;j--){ memset(dp,0xc0,sizeof(dp)); dp[0]=0; for(int k=1;k<=m;k++) { s[k]=s[k]+a[j][k]; if(dp[k-1]>=0&&k!=1){ zy[k]=zy[k-1]; dp[k]=dp[k-1]+s[k]; }else{ zy[k]=k; dp[k]=s[k]; } if(num<dp[k]){ l1=i,r1=j,l2=zy[k],r2=k; num=dp[k]; } sum2[j]=max(sum2[j],dp[k]); } } } for(int i=1;i<=n;i++) sum1[i]=max(sum1[i],sum1[i-1]); for(int i=n;i;i--) sum2[i]=max(sum2[i],sum2[i+1]); for(int i=1;i<=m;i++) sum3[i]=max(sum3[i],sum3[i-1]); for(int i=m;i;i--) sum4[i]=max(sum4[i],sum4[i+1]); for(int i=l1;i<=r1;i++) for(int j=l2;j<=r2;j++){ ans=min(ans,max(num-a[i][j]+p,max(max(sum1[i-1],sum2[i+1]),max(sum3[j-1],sum4[j+1])))); } printf("%d ",min(num,ans)); } return 0; }
区间dp+ (http://hihocoder.com/problemset/problem/1636)
题目大意:
有n堆石子,每次将连续L~R堆石子合并成一堆,合并的代价为这若干堆石子的石子个数总和。
将这n堆石子合并成1堆,要使得代价之和最小。
n<=50。
思路:
dp[l][r] = sum{al~ar} +min{ dp[l][k1]+dp[k1+1][k2]+dp[k2+1][k3] + dp[k3+1][r] } n^3
m个数分成L~R段,使得和最小。
g[x][y] 前x个数分成y段,和最小是多少。 枚举最后一段。 m^3
dp[l][r]是要把l-r之间的数分割,所以g[x][y]每固定一个l重新求一次,把l作为第一个点
n^5 l~r m个数 l~r+1 m+1个数 只要求g[m+1][?] ... n^4
有dp[i][j]=min{g[j][???]}
g[k][l]=min{g[t][l-1]+dp[t+1][k]}
代码:

#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; inline int read() { int x=0, w=1; char ch=getchar(); while (ch<'0' || ch>'9') { if (ch=='-') w=-1; ch=getchar(); } while (ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0', ch=getchar(); return x*w; } int n,l,r,a[104]; int g[104][104][104]; int main(){ while(scanf("%d%d%d",&n,&l,&r)!=EOF){ memset(dp,0x3f,sizeof(dp)); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); sum[i]=sum[i-1]+a[i]; dp[i][i]=1; } for(int k=2;k<=n;k++){ for(int i=1;i<=n-k+1;i++){ int j=k+i-1; for(int h=i;h<=j;h++){ g[i][k][h]= } return 0; }
D游戏 (http://acm.hdu.edu.cn/showproblem.php?pid=5693)
题目大意:
有n个数,每次可以删连续若干个数(2~3),要求它们是等差数列,且差值属 于集合A。
问最多能删多少数。 n<=300。
思路:
n个数 集合A给定 O(n^2) 预处理 f[i][j] a[j]-a[i] 是否属于集合A
法一:
dp[l][r] 表示l~r 这段区间 最多能删多少数
(1)dp[i][j]=dp[l][k]+dp[k+1][r] O(n)
(2)若存在一种解无法用(1)中1的方式转移,则必为l到r全选,此时有两种判断(转移)方式
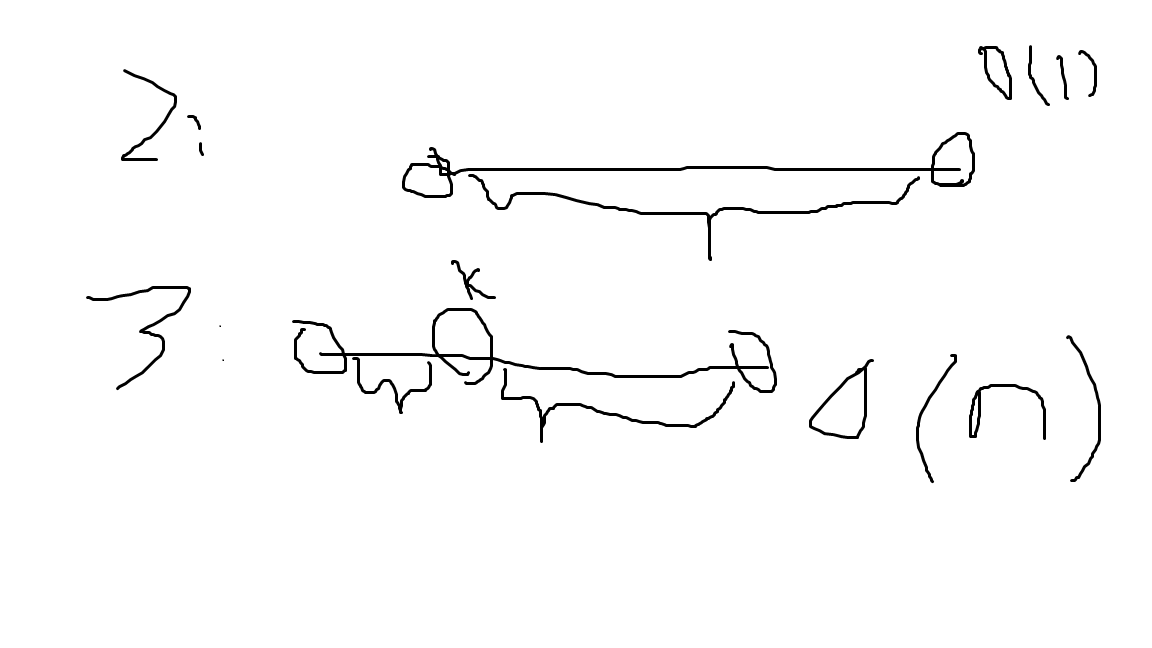
删若干个数可转换为一次删2或3个数,对于删两个数还是三个数,见下图。
两个数取dp[l+1][r-1]判断,三个数枚举中间的k,取dp[l+1][k-1],dp[k+1][r-1]判断
法二:
Dp[l][r] 能否被完全删完 找若干段互不相交的区间使得区间长度和最大。
D++ (http://acm.hdu.edu.cn/showproblem.php?pid=5712)
题目大意:
有n个数,每次可以删连续若干个数(L~R),要求它们是等差数列,且差值属于集合A。
问最多能删多少数。
n<=30。
思路:
上题的2~3变为本题的l~r,枚举中间点???
状压DP
特点:N!过不了,2^N或3^N可以过,常用3^N枚举子集
过桥问题
题目大意:
有n个人,第i个人的体重是ai,过一座桥的时间为bi。
有一座桥,承重是w。
它们只能一批一批过桥,时间算最慢的那个人的时间。
求最少多少时间能让所有人过桥。
n<=16。
思路:
f[i] 还有i这个状态的人没过桥,最少还需要多少时间
枚举j这个状态的人一起过桥, f[i]=f[i-j]+work(j) 3^n
v[i] i这个状态中1的个数
可以用v[i]排序循环枚举,也可以直接顺序循环枚举
for (i=1; i<(1<<n); i++) for (j=(i-1&i); j; j=(j-1&i)) ...
交换茸角(BZOJ)https://darkbzoj.cf/problem/3900
题目大意:
有n头鹿,每个鹿有两只角,每只角有重量。
每次可以交换两只角,求最少操作次数使得每只鹿的两只角重量之差<=k。
n<=16。
思路:
• 怎么判断是否有解 ? 排个序
• 答案的上限? n-1次
• f[i] 表示 只考虑i这个状态的鹿,最少需要交换几次。
• 先判断是否有解, 不存在f[i]=inf
存在f[i]=v[i]-1 // v[i] = i中1的个数
枚举i的子集j, f[i]=min{f[i],f[j]+f[i-j]} 3^n
DP套DP
把一个未知量变成已知量后仍为DP
Hero meet devil (http://acm.hdu.edu.cn/showproblem.php?pid=4899)
题目大意:
有一个字符串T,k=|T|<=15。
有一个未知的字符串S,问对于所有i,有多少个S和T的最长公共子序列=i。
S和T只包含{'A','C','T','G'}。
给定S的长度,保证<=1000。
思路:
1. 当已知S时,怎么做?
dp[i][j] S到了i这一位,T到了j这一位, 此时最长公共子序列是多少
=max(dp[i-1][j],dp[i][j-1]) , S[i]==T[j] dp[i-1][j-1]+1
dp[i][?] S[i]是什么 dp[i-1][?]是什么
f[i][t0][t1][t2]...[tk] 当前已经做到了S的前i位,并且此时dp[i][0]是t0,dp[i][1]是t1,...,dp[i][k]是tk,有多少方案。
枚举S的第i+1位 来算出 dp[i+1][?]
f[|S|][t0][t1][t2]..[tk] 存在多少S,使得和T的最长公共子序列是tk。
tx S的前i位和T的前x位的最长公共子序列
tx <= t{x+1} <= tx +1
只要记录差,就能够还原tx。差是非0即1
2^15 来记录这个差
g[t][‘A’|’C’...] 从t这个状态出发,下一个字符是什么,能得到什么样的新状态。
f[i][?] -> f[i+1][g[?][‘A’,...,]]
首先假设已知S,有dp[i][j]=max{dp[i-1][j],dp[i-1][j]},dp[i-1][j-1]+1
第三项需要满足一定条件。
现在不知道S,发现这个dp状态只依赖于S和T的第i位和dp[i-1][?]。
也就是说,当这些都已知时,dp就是可以被计算的。
将dp[i-1][?]打包成一个状态即可。
最短路计数http://www.51nod.com/Challenge/Problem.html#!#problemId=1683
题目大意:
一个未知的01矩阵。一个人从左上角走到右下角,可以往下右上走。
经过“1”会耗费1点能量。
已知从左上角到右下角最少耗费能量。问这个01矩阵的方案总数。方案总数对p取模。
n<=6,m<=100。
思路:
•矩阵已知,求最短路
•dp[i][j] 起点到 第i列,第j行的最短路 得知道 矩阵第i列的情况,以及dp[i-1][?] 的信息
•f[i][t1]...[tk] 到第i行,dp[i][1]=t1,dp[i][k]=tk 这样的方案总数 枚举第i+1列,求 出后面k维,更新。 100 * 100 * 3^5 * 2^6
转移方式预处理???好像
tx与t{x+1}之间相差-1,0,1,状态压缩差值,三进制即可,三进制可先初始化
数位DP
基本格式:dp[i][0/1]表示搜到第i位,截至目前是<n还是=n的数个数,有几个限制加几维
另一种数位dp
题目大意:
给定一个数n,将n分成三个数A,B,C,使得每个数都不包含数字3,且 A+B+C=n,求方案总数,答案对p取模。 n<=10^1000。
思路:
dp[i][x] 考虑前i位,还需要从后往前向上进x位 。x= 0,1,2.
枚举第i+1位,A,B,C分别是什么。
LIS问题
题目大意:
设一个数的LIS为该数各位拆开来后的最长上升子序列。例如1324的LIS为3。
求l~r中LIS为k的数的个数。
1<=l<=r<=10^18。
思路:
先了解一种求LIS的方法:
dp[i]为以<=i为结尾的最长子序列长度,显然满足dp[i]<=dp[i+1]<=dp[i]+1
来看这道题:
f[i][0/1] [t0]..[t9] 考虑了前i位,并且和r的等于/小于
dp[0]=t0,dp[1]=t1 ,..., dp[9]=t9 这样的方案总数
枚举第i+1位是什么,转移方式预处理
18 * 10! * 10
又因dp[i] <= dp[i+1] <=dp[i]+1 ,维护差值,18*2^10*10。
LIS问题2 (BZOJ3591)
题目大意:
给出一个1~n排列的其中一种最长上升子序列,求原序列可能的种数。
n<=15。
思路:
同上f[i][t0][t1]...[tk] - > f[i][j]
i代表选了i这个状态的数,j代表n维dp差值的十进制形式
n可以优化为v[i],v[i]表示i的二进制数中有多少个1
枚举x,判断是否合法(若n是序列中的数,判断dp[n]是否与它在给定序列中的rank 相等)
在全找完后再判断最大子序列长度是否等于其给定序列长度
blocks
题目大意:
有一排砖,数量为N。现要将砖全部染上色,有红、蓝、绿、黄四种颜色。要求被染成红色和绿色的砖块数量必须为偶数,问一共有多少种染色方案。(由于答案较大,模10007)
N<=10^9。
思路:
dp[i][0/1][0/1] 前i个砖,红 奇/偶,绿 奇/偶
dp[i+1][0][0]=2*dp[i][0][0]+dp[i][0][1]+dp[i][1][0]
……
<(0,0),(0,1),(1,0),(1,1)> * M = <[0,0],[0,1],[1,0],[1,1]>
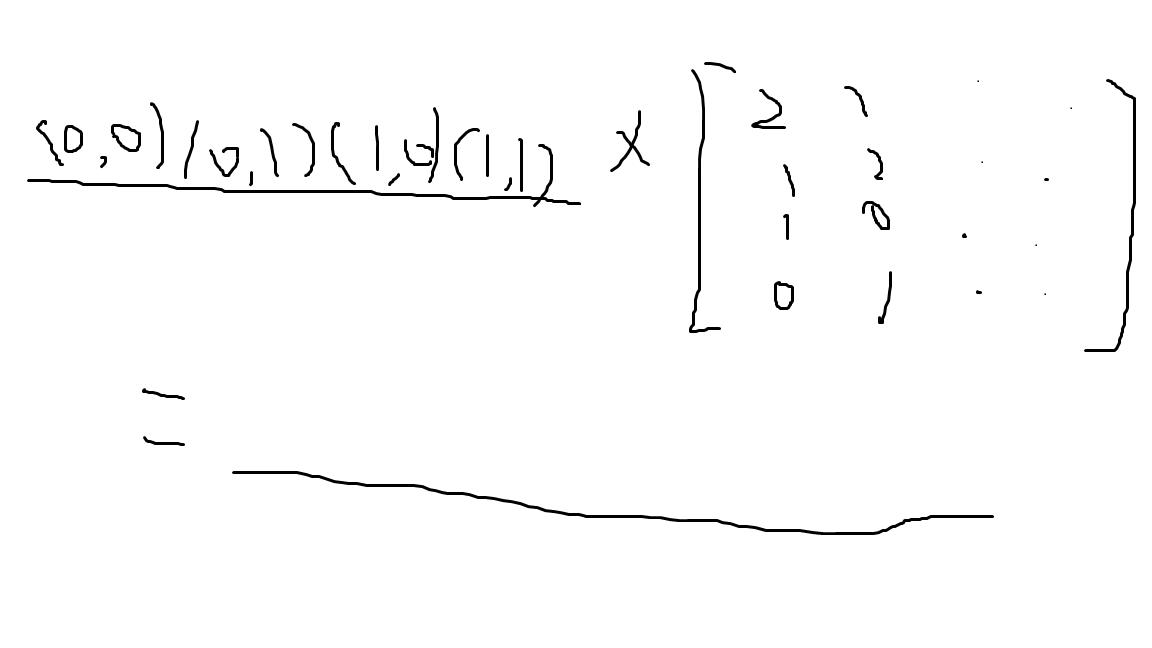
4^3*logn
PKU校测
题目大意:
有100根灯管,要么亮要么暗。
给定初始状态和目标状态。
有两种操作:
1.选择一根,转换它的状态。
2.选择两根,装换它们的状态。
总共可以操作k步,求方案总数对1e9+7取模后的结果。
k<=1e9。
思路:
dp[i][j] 表示操作i步后,有j根灯管已经符合条件了。
dp[i][j] = dp[i-1][j-2] ~ dp[i-1][j+2]
矩阵优化同上
100k
https://www.luogu.org/problemnew/show/P3647
oil https://www.cnblogs.com/zbtrs/p/8491115.html
