最小生成树

1.是一棵树

　　无回路

　　|V|个顶点一定有|V|-1条边

2.是生成树

　　包含全部顶点

　　|V|-1条边都在图里

3.边的权重和最小

最小生成树存在<->图连通

贪心算法

　　贪：每一步都是最好的

　　好：权重最小的边

　　约束：只能用图里的边、正好用掉|V|-1条边、不能有回路

Prim算法—让一颗小树长大

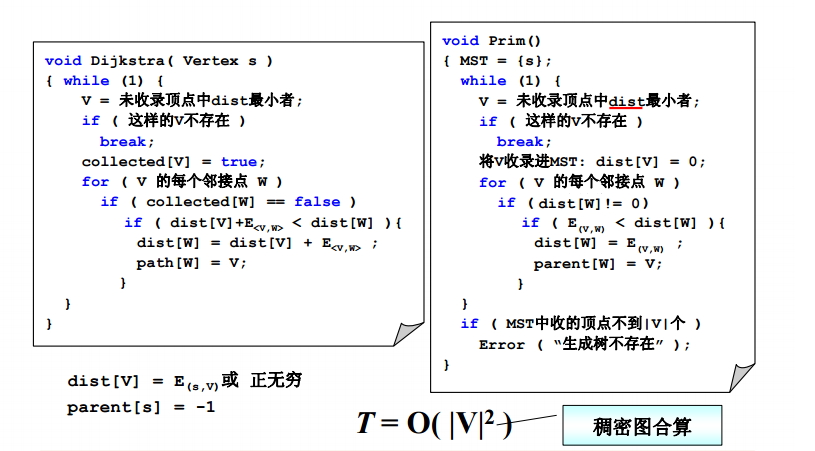
代码：

//邻接矩阵存储 Prim最小生成树算法

void Prim(MGraph *G, int Parent[])
{
    //默认从序号0出发
    //每个顶点的父节点的最小生成树存于数组Parent中
    int Dist[MaxVertexNum];
    int i, j, k;

    for (i = 1; i < G->n; i++) {
        Dist[i] = G->Edges[0][i];
        Parent[i] = 0;
    }
    Dist[0] = 0;  //从序号0开始构造最小生成树
    Parent[0] = -1;
    for (i = 1; i < G->n; i++)  //还需要收集n-1个顶点
    {
        k = FindMin(Dist, G->n); //找出V-Vt中到Vt最小距离的点 与树最小距离
        if (k) {
            Dist[k] = 0; //生长至顶点k 表示已经收录
            for (j = 1; j < G->n; j++) //更新当前最小生成树
                if (Dist[j] && G->Edges[k][j] < Dist[j])
                {  //如果该顶点未被收录且距离需要更新
                    Dist[j] = G->Edges[k][j];
                    Parent[j] = k;
                }
        }
        else {
            //没收集完所有结点就不能继续生长，一定为非连通图
            printf("图不连通");
            break;
        }
    }
}

int FindMin(int Dist[], int n)
{
    int i, MinV = 0;
    int MinDist = INFINITY;
    for (i = 0; i < n; i++)
        if (Dist[i] && Dist[i] < MinDist)
        {
            MinDist = Dist[i];
            MinV = i;
        }
    return MinV;
}

时间复杂度：第一个for循环|V|-1 第二个for循环里又要执行FindMin和一个for 次数为2(|V|-1)^2 时间复杂度T = O(|V|^2) 对稠密图较好

Kruskal算法—将森林合成树

代码：

  1 /* 邻接表存储 - Kruskal最小生成树算法 */
  2  
  3 /*-------------------- 顶点并查集定义 --------------------*/
  4 typedef Vertex ElementType; /* 默认元素可以用非负整数表示 */
  5 typedef Vertex SetName;     /* 默认用根结点的下标作为集合名称 */
  6 typedef ElementType SetType[MaxVertexNum]; /* 假设集合元素下标从0开始 */
  7  
  8 void InitializeVSet( SetType S, int N )
  9 { /* 初始化并查集 */
 10     ElementType X;
 11  
 12     for ( X=0; X<N; X++ ) S[X] = -1;
 13 }
 14  
 15 void Union( SetType S, SetName Root1, SetName Root2 )
 16 { /* 这里默认Root1和Root2是不同集合的根结点 */
 17     /* 保证小集合并入大集合 */
 18     if ( S[Root2] < S[Root1] ) { /* 如果集合2比较大 */
 19         S[Root2] += S[Root1];     /* 集合1并入集合2  */
 20         S[Root1] = Root2;
 21     }
 22     else {                         /* 如果集合1比较大 */
 23         S[Root1] += S[Root2];     /* 集合2并入集合1  */
 24         S[Root2] = Root1;
 25     }
 26 }
 27  
 28 SetName Find( SetType S, ElementType X )
 29 { /* 默认集合元素全部初始化为-1 */
 30     if ( S[X] < 0 ) /* 找到集合的根 */
 31         return X;
 32     else
 33         return S[X] = Find( S, S[X] ); /* 路径压缩 */
 34 }
 35  
 36 bool CheckCycle( SetType VSet, Vertex V1, Vertex V2 )
 37 { /* 检查连接V1和V2的边是否在现有的最小生成树子集中构成回路 */
 38     Vertex Root1, Root2;
 39  
 40     Root1 = Find( VSet, V1 ); /* 得到V1所属的连通集名称 */
 41     Root2 = Find( VSet, V2 ); /* 得到V2所属的连通集名称 */
 42  
 43     if( Root1==Root2 ) /* 若V1和V2已经连通，则该边不能要 */
 44         return false;
 45     else { /* 否则该边可以被收集，同时将V1和V2并入同一连通集 */
 46         Union( VSet, Root1, Root2 );
 47         return true;
 48     }
 49 }
 50 /*-------------------- 并查集定义结束 --------------------*/
 51  
 52 /*-------------------- 边的最小堆定义 --------------------*/
 53 void PercDown( Edge ESet, int p, int N )
 54 { /* 改编代码4.24的PercDown( MaxHeap H, int p )    */
 55   /* 将N个元素的边数组中以ESet[p]为根的子堆调整为关于Weight的最小堆 */
 56     int Parent, Child;
 57     struct ENode X;
 58  
 59     X = ESet[p]; /* 取出根结点存放的值 */
 60     for( Parent=p; (Parent*2+1)<N; Parent=Child ) {
 61         Child = Parent * 2 + 1;
 62         if( (Child!=N-1) && (ESet[Child].Weight>ESet[Child+1].Weight) )
 63             Child++;  /* Child指向左右子结点的较小者 */
 64         if( X.Weight <= ESet[Child].Weight ) break; /* 找到了合适位置 */
 65         else  /* 下滤X */
 66             ESet[Parent] = ESet[Child];
 67     }
 68     ESet[Parent] = X;
 69 }
 70  
 71 void InitializeESet( LGraph Graph, Edge ESet )
 72 { /* 将图的边存入数组ESet，并且初始化为最小堆 */
 73     Vertex V;
 74     PtrToAdjVNode W;
 75     int ECount;
 76  
 77     /* 将图的边存入数组ESet */
 78     ECount = 0;
 79     for ( V=0; V<Graph->Nv; V++ )
 80         for ( W=Graph->G[V].FirstEdge; W; W=W->Next )
 81             if ( V < W->AdjV ) { /* 避免重复录入无向图的边，只收V1<V2的边 */
 82                 ESet[ECount].V1 = V;
 83                 ESet[ECount].V2 = W->AdjV;
 84                 ESet[ECount++].Weight = W->Weight;
 85             }
 86     /* 初始化为最小堆 */
 87     for ( ECount=Graph->Ne/2; ECount>=0; ECount-- )
 88         PercDown( ESet, ECount, Graph->Ne );
 89 }
 90  
 91 int GetEdge( Edge ESet, int CurrentSize )
 92 { /* 给定当前堆的大小CurrentSize，将当前最小边位置弹出并调整堆 */
 93  
 94     /* 将最小边与当前堆的最后一个位置的边交换 */
 95     Swap( &ESet[0], &ESet[CurrentSize-1]);
 96     /* 将剩下的边继续调整成最小堆 */
 97     PercDown( ESet, 0, CurrentSize-1 );
 98  
 99     return CurrentSize-1; /* 返回最小边所在位置 */
100 }
101 /*-------------------- 最小堆定义结束 --------------------*/
102  
103  
104 int Kruskal( LGraph Graph, LGraph MST )
105 { /* 将最小生成树保存为邻接表存储的图MST，返回最小权重和 */
106     WeightType TotalWeight;
107     int ECount, NextEdge;
108     SetType VSet; /* 顶点数组 */
109     Edge ESet;    /* 边数组 */
110  
111     InitializeVSet( VSet, Graph->Nv ); /* 初始化顶点并查集 */
112     ESet = (Edge)malloc( sizeof(struct ENode)*Graph->Ne );
113     InitializeESet( Graph, ESet ); /* 初始化边的最小堆 */
114     /* 创建包含所有顶点但没有边的图。注意用邻接表版本 */
115     MST = CreateGraph(Graph->Nv);
116     TotalWeight = 0; /* 初始化权重和     */
117     ECount = 0;      /* 初始化收录的边数 */
118  
119     NextEdge = Graph->Ne; /* 原始边集的规模 */
120     while ( ECount < Graph->Nv-1 ) {  /* 当收集的边不足以构成树时 */
121         NextEdge = GetEdge( ESet, NextEdge ); /* 从边集中得到最小边的位置 */
122         if (NextEdge < 0) /* 边集已空 */
123             break;
124         /* 如果该边的加入不构成回路，即两端结点不属于同一连通集 */
125         if ( CheckCycle( VSet, ESet[NextEdge].V1, ESet[NextEdge].V2 )==true ) {
126             /* 将该边插入MST */
127             InsertEdge( MST, ESet+NextEdge );
128             TotalWeight += ESet[NextEdge].Weight; /* 累计权重 */
129             ECount++; /* 生成树中边数加1 */
130         }
131     }
132     if ( ECount < Graph->Nv-1 )
133         TotalWeight = -1; /* 设置错误标记，表示生成树不存在 */
134  
135     return TotalWeight;
136 }

点这里看代码

竞赛代码：

//第i条边的两个端点序号和权值分别存在u[i],v[i]和w[i]中
//排序后的第i小的边的序号保存在r[i]中
int cmp(const int i, const int j)
{
    return w[i] < w[j];
}
int Find(int x)
{
    return p[x] == x ? x : p[x] = Find(p[x]);
}
int Kruskal()
{
    int ans = 0;
    for (int i = 0; i < n; i++)//初始化并查集
        p[i] = i;
    for (int i = 0; i < m; i++) //初始化边序号
        r[i] = i;
    sort(r, r+m, cmp); //给边排序
    for (int i = 0; i < m; i++) {
        int e = r[i];
        int x = Find(u[e]);
        int y = Find(v[e]);
        if (x != y) {
            ans += w[e];
            p[x] = y;
        }
    }
    return ans;
}