NFA的确定化
该方法称为子集法:
按字符将起始状态集与到达状态集抽象为状态,从而等价地化为单值映射, ε弧按照语义被吸收,由 ε-closure 运算去除
首先定义 ε-closure 运算:
设 I 是状态集的一个子集,则 I 的 ε-闭包 ε-closure(I) 为
- 若状态s∈I,则s∈ε-closure(I)
- 若状态s∈I,则从s出发经过任意条 ε弧可以到达的任何状态s’,都属于ε-closure(I)
再定义Ia运算:
设a为Σ中的一个字符,定义Ia=ε-closure(J),其中,
J为I中的某个状态出发经过一条a弧而到达的状态集合,Ia即是为这样的集合作ε-闭包
以下图的NFA为例,说明ε-闭包及Ia运算

ε-closure({1}) = {1,2}
记 I = {1,2},则 Ia= ε-closure({5,4,3}) = {5,4,3,6,2,7,8}
在下图NFA中使用子集法进行确定化
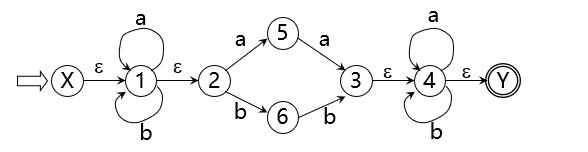
如下表,表头为参与计算的状态集 I,各字符的运算结果 Ii,其中i∈Σ
每个计算出的状态集再进行 Ii 的运算、
因为Σ为有限集,所以这张表也是有限的
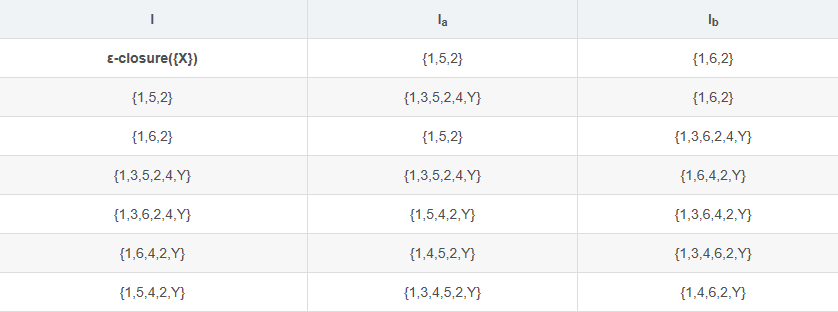
这张表实际上就是状态集 I 接收字符 i 后到达状态集 Ii,描述了状态集间的单值映射
将每个状态集视为新的状态,该表即为一个状态转换矩阵
这个状态转换矩阵就是一个新的FA,而且是一个DFA
其中含有原先初态X的状态集为新的初态,含有原来任何一个终态的状态集都是新的终态
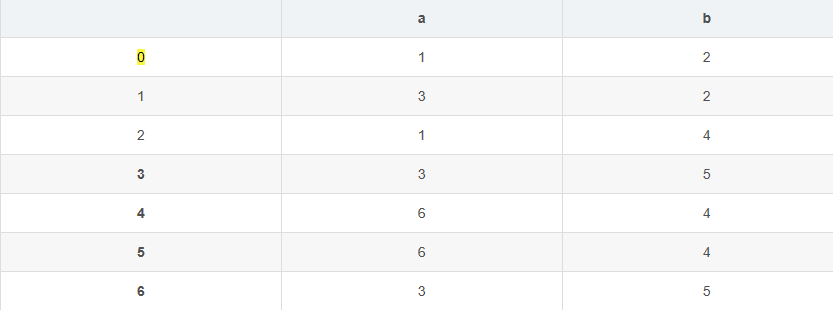
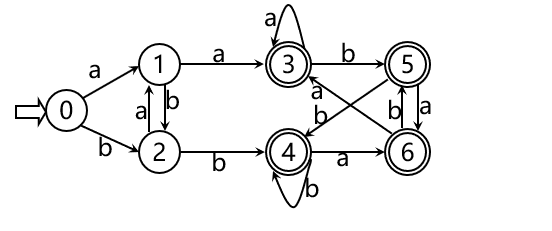
不难看出,这就是识别含有aa或bb的字的DFA
那么,现在的词法分析的理论已经是下面酱紫了
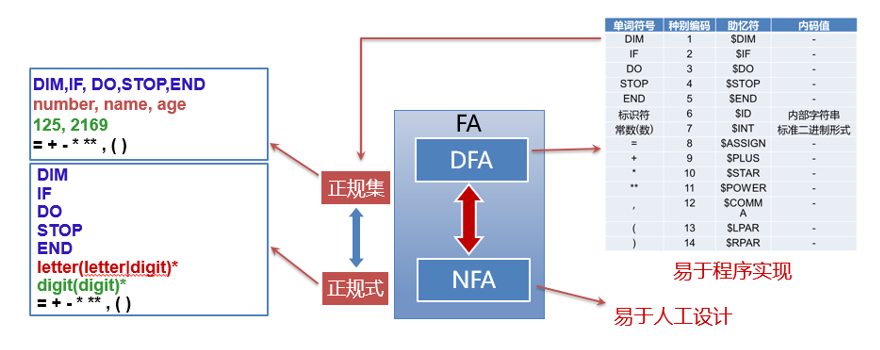
小结:程序设计语言的单词集合是一个正规集,可以由正规式描述,正规式与正规集是一组对应的概念;FA分为DFA和NFA,NFA易于人工设计,DFA易于词法分析的程序实现,从定义上来看,DFA是NFA的特例,而NFA与DFA的描述是相同的,并且NFA可以等价地转换为DFA
DFA的化简即是状态集按等价类的划分
- 使任何两个不同的子集中的状态是可区分的,而同一状态中的任意状态间是等价的
- 任何两个子集均不相交
- 最后每个子集保留一个状态
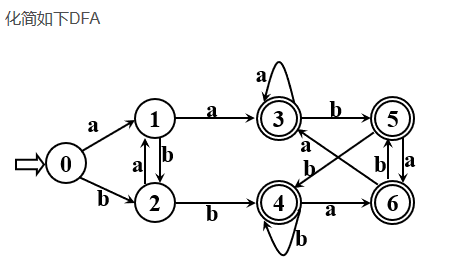
I = {0,1,2,3,4,5,6},其中终态为{3,4,5,6}
∴初始划分为 I(1) = {3,4,5,6},I(2) = {0,1,2}
等待划分的子集有 I(1)、I(2),Π = {I(1),I(2)}
检查 I(1) 是否可以按字符 a 或 b 进行划分,Ia(1)包含于 I(1) ,Ib(1)也包含于 I(1) , 即 I(1) 中各状态是等价的,无须划分
等待划分的子集有 I(2),Π = {I(1),I(2)}
检查 I(2) 是否可以按字符 a 进行划分,Ia(2) = {1,3},分别落在I(1)和I(2)中, 因此将 I(2) 划分为 I(21) = {0,2},I(22) = {1}
等待划分的子集有 I(21)、I(22),Π = {I(1),I(21), I(22)}
检查 I(21) 是否可以按字符 a 划分,(其实已经检查过了 ), Ia(21) 包含于 I(22), 检查 I(21) 是否可以按字符 b 划分,Ib(2) = {2,4},分别落在 I(21) 和 I(1) 中, 因此将 I(21) 划分为 I(211) = {0}, I(212) = {2}
等待划分的子集有 I(22)、I(211)、I(212),Π = {I(1),I(22),I(211),I(212)}
I(22)大小为1,无须继续划分 I(211)大小为1,无须继续划分 I(212)大小为1,无须继续划分
划分完毕,Π = {I(1),I(22),I(211),I(212)} I(1) = {3,4,5,6},I(22) = {1},I(211) = {0},I(212) = {2}
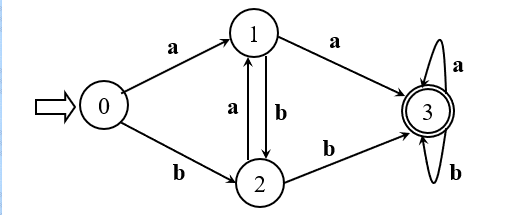
则保留状态 0、1、2、3,其中0为初态,3为终态 按照转换关系,得到化简结果如下
原文链接:https://blog.csdn.net/kafmws/article/details/96595750