条件随机场

马尔可夫随机场

概率图模型是由图表示的概率分布。概率无向图模型又称马尔可夫随机场（Markov random field），表示一个联合概率分布，其标准定义为：

设有联合概率分布(P(V))由无向图(G=(V, E))表示，图(G)中的节点表示随机变量，边表示随机变量间的依赖关系。如果联合概率分布(P(V))满足成对、局部或全局马尔可夫性，就称此联合概率分布为概率无向图模型或马尔可夫随机场。

成对马尔可夫性

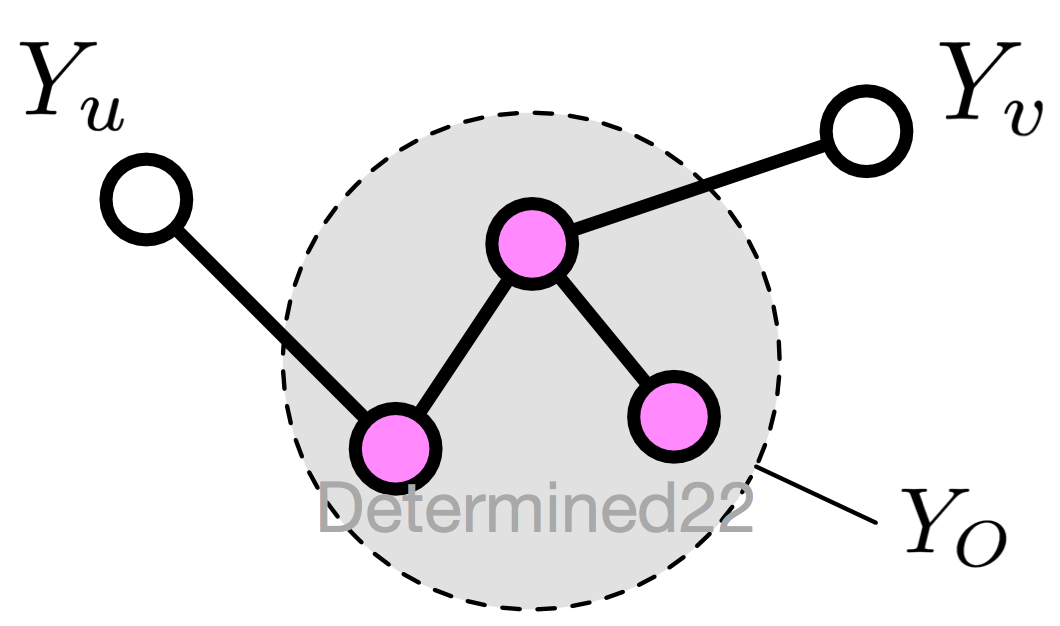
设无向图(G)中的任意两个没有边连接的节点(u),(v) ，其他所有节点为(O)，成对马尔可夫性指：给定(Y_O)的条件下，(Y_u)和(Y_v)条件独立

[P(Y_u,Y_v|Y_O)=P(Y_u|Y_O)P(Y_v|Y_O) ]

局部马尔可夫性

设无向图(G)的任一节点(v)，(W)是与(v)有边相连的所有节点，(O)是(v)、(W)外的其他所有节点，局部马尔可夫性指：给定(Y_W)的条件下，(Y_v)和(Y_O)条件独立

全局马尔可夫性

设节点集合(A)、(B)是在无向图(G)中被节点集合(C)分开的任意节点集合，全局马尔可夫性指：给定(Y_C)的条件下，(Y_A)和(Y_B)条件独立

条件随机场

条件随机场的定义

条件随机场

设(X)和(Y)是随机变量，(P(Y|X))是在给定(X)的条件下(Y)的条件概率分布。若随机变量(Y)构成一个有无向图(G=(V,E))表示的马尔可夫场，即

[P(Y_v|X,Y_w,w eq v)=P(Y_v|X,Y_w, w sim v) ]

对任意节点(v)都成立，则称(P(Y|X))是条件随机场。式中(w≠v)表示(w)是除(v)以外的所有节点，(w∼v)表示(w)是与(v)相连接的所有节点。

线性链条件随机场

对于线性链条件随机场来说，图(G)的每条边都存在于状态序列(Y)的相邻两个节点，最大团(C)是相邻两个节点的集合，(X)和(Y)有相同的图结构意味着每个(X_i)都与(Y_i)一一对应。

设(X=(X_1,...,X_n),Y=(Y_1,...,Y_n))均为线性链表示的随机变量序列，若在给定随机变量序列(X)的条件下，随机变量序列(Y)的条件分布(P(Y|X))构成条件随机场，即满足马尔可夫性

[P(Y_i|X,Y_1,cdots,Y_{i−1},Y_{i+1},cdots,Y_n)=P(Y_i|X,Y_{i−1},Y_{i+1}), \ i=1,cdots,n quad ext{其中当$i$取1或$n$时只考虑单边}]

则称(P(Y|X))为线性链条件随机场。在标注问题中(X)表示输入观测序列，(Y)表示对应的状态序列。

条件随机场的形式

参数化形式

设(P(Y|X))为线性链条件随机场，则在随机变量(X)取值为(x)的条件下，随机变量(Y)取值为(y)的条件概率具有如下形式：

[P(y|x)=frac{1}{Z(x)}exp left[ sum_{i,k}lambda_kt_k(y_{i-1},y_i,x,i)+sum_{i,l}mu_ls_l(y_i,x,i) ight] ]

其中

[Z(x)=sum_{y}exp left[ sum_{i,k}lambda_kt_k(y_{i-1},y_i,x,i)+sum_{i,l}mu_ls_l(y_i,x,i) ight] ]

式中，(t_k)和(s_t)是特征函数，(lambda_k)和(mu_l)是对应的权值。

上式是基本形式，表示给定输入序列(x),对输出序列(y)预测的条件概率。(t_k)是定义在边上的特征函数，称为转移特征，依赖于当前和前一个位置，(s_l)是定义在节点上的特征函数，称为状态特征，依赖于当前位置。(t_k)和(s_l)都依赖于位置，是局部特征函数。通常都是0-1函数。

线性链条件随机场也是对数线性模型(逻辑回归也是)。

简化形式

将转移特征和状态特征机器权值用统一的符号表示。设有(K_1)个转移特征，(K_2)个状态特征，(K=K_1+K_2)，记

[f_k(y_{i-1},y_i,x,i)=egin{cases} t_k(y_{i-1},y_i,x,i) quad k=1,2,cdots,K_1 \ s_l(y_i,x,l) quad k=K_1+l; l=1,2,cdots,K_2 end{cases}]

然后，对转移与状态特征在各个位置(i)求和，记作

[f_k(y,x)=sum limits_{i=1}^n f_k(y_{i-1},y_i,x,i),quad k=1,2,cdots,K ]

用(w_k)表示特征(f_k(y,x))的权值，即

[w_k=egin{cases} lambda_k, quad k=1,2cdots,K_1 \ mu_l, quad k=K_1+l, l=1,2,cdots,K_2 end{cases}]

于是，条件随机场可以表示为

[p(y|x)=frac{1}{Z_y(x)}exp sum_{k=1}^K w_kf_k(y,x) ]

还可以把(w_k)和(f_k(y,x))表示成向量的形式

矩阵形式

引进特殊的起点和和终点状态标记(y_0=start,y_{n+1}=stop)，这是(P_w(y|x))(简化形式)可以通过矩阵形式表示

对观测序列(x)的每一个位置(i=1,2,cdots,n+1)，定义一个(m)阶的矩阵(m是标记(y_i)取值的个数)

[M_i(x)=[M_i(y_{i-1},y_i|x)] ]

[M_i(y_{i-1},y_i|x)=exp(W_i(y_{i+1,y_i|x})) ]

[W_i(y_{i+1},y_i|x)=sum_{k=1}^K w_kf_k(y_{i-1},y_i,x,i) ]

这样，给定观测序列(x)，相应标记序列(y)的非规范化概率可以通过该序列(n+1)个矩阵适当元素的乘积(prod_{i=1}^{n+1}M_i(y_{i-1},y_i|x))表示，于是条件概率(P_w(y|x))是

[P_w(y|x)=frac{1}{Z_w(x)}prod_{i=1}^{n+1}M_i(y_{i-1},y_i|x) ]

其中，(Z_w(x))是规范化因子，是(n+1)个矩阵的乘积的(start，stop)元素。

[Z_w(x)=(M_1(x)M_2(x)cdots M_{n+1}(x))_{start,stop} ]

注意，(y_0=start)与(y_{n+1}=stop)表示开始开始状态和终止状态，规范化因子(Z_w(x))是以start为起点stop为终点通过状态的所有路径(y_1 y_2 cdots y_n)的非规范化概率(prod_{i=1}^{n+1}M_i(y_{i-1},y_i|x))之和。