//bzoj上的题面太丑了,导致VJ的题面也很丑,于是这题用洛谷的题面
题面描述
XOR(异或)是一种二元逻辑运算,其运算结果当且仅当两个输入的布尔值不相等时才为真,否则为假。 XOR 运算的真值表如下((1) 表示真, (0) 表示假):
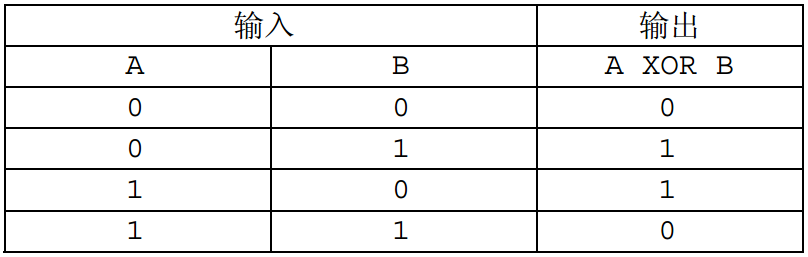
而两个非负整数的 XOR 是指将它们表示成二进制数,再在对应的二进制位进行 XOR 运算。
譬如 (12) XOR (9) 的计算过程如下:
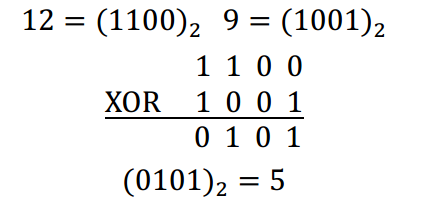
故 (12) XOR (9) = 5$。
容易验证, XOR 运算满足交换律与结合律,故计算若干个数的 XOR 时,不同的计算顺序不会对运算结果造成影响。从而,可以定义 (K) 个非负整数 (A_1,A_2,……,A_{K-1},A_K)的 XOR 和为
(A_1) XOR (A_2) XOR …… XOR (A_{K-1}) XOR (A_K)
考虑一个边权为非负整数的无向连通图,节点编号为 (1) 到 (N),试求出一条从 (1) 号节点到 (N) 号节点的路径,使得路径上经过的边的权值的 XOR 和最大。
路径可以重复经过某些点或边,当一条边在路径中出现了多次时,其权值在计算 XOR 和时也要被计算相应多的次数,具体见样例。
输入格式
输入文件 xor.in 的第一行包含两个整数 (N) 和 (M), 表示该无向图中点的数目与边的数目。
接下来 (M) 行描述 (M) 条边,每行三个整数 (S_i), (T_i) , (D_i), 表示 (S_i) 与 (T_i) 之间存在一条权值为 (D_i) 的无向边。
图中可能有重边或自环。
输出格式
输出文件 xor.out 仅包含一个整数,表示最大的 XOR 和(十进制结果)。
输入输出样例
输入 #1
5 7
1 2 2
1 3 2
2 4 1
2 5 1
4 5 3
5 3 4
4 3 2
输出 #1
6
说明/提示
【样例说明】
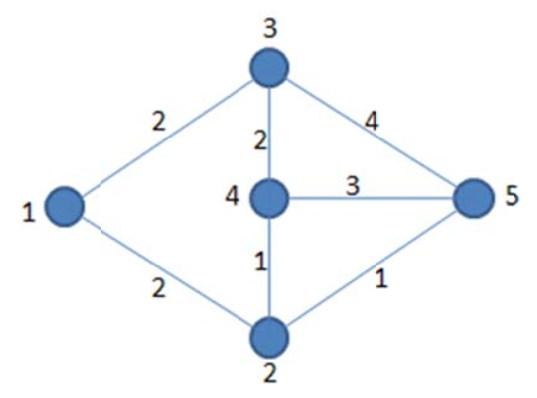
如图,路径(1 ightarrow 2 ightarrow 4 ightarrow 3 ightarrow 5 ightarrow 2 ightarrow 4 ightarrow 5)对应的XOR和为
(2) XOR (1) XOR (2) XOR (4) XOR (1) XOR (1) XOR (3 = 6)
当然,一条边数更少的路径(1 ightarrow 3 ightarrow 5)对应的XOR和也是(2) XOR (4 = 6)。
【数据规模】
对于 (20 \%) 的数据,(N leq 100,M leq 1000,D_i leq 10^{4});
对于 (50 \%) 的数据,(N leq 1000,M leq 10000,D_i leq 10^{18});
对于 (70 \%) 的数据,(N leq 5000,M leq 50000,D_i leq 10^{18});
对于 (100 \%) 的数据,(N leq 50000), (M leq 100000),(D_i leq 10^{18})。
解题思路
看了题解可知,这题先dfs一遍图,随便找一条从起点到终点的路,求出路上的异或值,同时把所有搜索到的环的异或值全部加入线性基,然后把那条路上的异或值放到线性基里,找能够异或到的最大值,然后就是答案。敷衍
这题的思想有点像我这学期高数刚学的格林公式,不知道的就别管这个词了。我们从那条路起点(1)出发,到达路中间的一个点(x),然后离开这条路,通过某一段 (x ightarrow y) 走到某个环上的一个点(y),然后从点(y)开始绕环一周,回到点(y),再从点(y)通过刚才那段(y ightarrow x) 回到点(x),再接着走完那条路剩下的部分(x ightarrow n)。由“异或两次同一个数相当于没有异或”的性质可以知道,(x ightarrow y)和(y ightarrow x)就互相抵消了,于是答案就是(1 ightarrow n)的异或值再异或上那个环的异或值。再多走几个环,就再多异或几个环就好。
那么为什么最开始随便选一条路就好呢?是这样:假设存在两条路可以从(1)到(n),那么因为是无向图,这两条路就成了一个环,我们dfs过程中就会把这个环加入线性基。走了其中一条路,再走这个环,就相当于走了另一条路。
源代码
#include<stdio.h>
const int MAXN=5e5+5,MAXM=4e5+5;
typedef long long ull;
int n,m;
struct Edge{
int nxt,to;
ull w;
}e[MAXM<<1];
int cnt=1,head[MAXN];
inline void add(int u,int v,ull w)
{
e[cnt]={head[u],v,w};
head[u]=cnt++;
e[cnt]={head[v],u,w};
head[v]=cnt++;
}
ull b[64]={0};//线性基
inline void addb(ull a)
{
for(int i=62;~i;i--)
{
if(a>>i)
{
if(b[i]) a^=b[i];
else
{
b[i]=a;
return;
}
}
}
}
inline ull mx(ull ans)
{
for(int i=62;~i;i--)
if((ans^b[i])>ans) ans^=b[i];
return ans;
}
bool vis[MAXN];
ull dis[MAXN];//从1搜过来的值
void dfs(int u)
{
vis[u]=1;
for(int i=head[u];i;i=e[i].nxt)
{
int v=e[i].to;
if(vis[v])
addb(dis[v]^dis[u]^e[i].w);
else
{
dis[v]=dis[u]^e[i].w;
dfs(v);
}
}
}
int main()
{
//freopen("test.in","r",stdin);
scanf("%d%d",&n,&m);
while(m--)
{
int u,v;
ull w;
scanf("%d%d%lld",&u,&v,&w);
add(u,v,w);
}
dfs(1);
printf("%lld
",mx(dis[n]));
return 0;
}