
在初始化加边时可以把点权下放到边权(即为两个点中小的点权),然后可以发现所有符合条件的路径都是在最大生成树上。所以考虑$kruskal$。
可是最大生成树后难道又是暴力跑最短路吗?我们考虑到$kruskal$算法的实质,把所有边按边权从大到小排序,每次判断当前边权最大的边的两端点是否已经在个并查集中,如果没有就合并两个并查集。而当前加入的这条边权一定是之前已经加入的所有边中边权最小的!根据题意可以发现,需要合并的这两个并查集中两两个元素相互之间的高兴值就是这条边的边权。所以再维护一个并查集的$size$,每次合并$u$和$v$时,当前边的贡献就是$u$所在并查集的$size*v$所在并查集的$size*$边权。
需要一些常数优化不然会tle。
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<queue> #define RG register #define ll long long using namespace std; int n, m; void read ( int &x ) { x = 0; char ch = getchar ( ); while ( ch > '9' || ch < '0' ) ch = getchar ( ); while ( ch >= '0' && ch <= '9' ) { x = x * 10 + ch - '0'; ch = getchar ( ); } } struct egde { int u, v, nex, w; } init[2000005]; int stot_init, h_init[100005]; void add_init ( int u, int v, int s ) { init[++stot_init].v = v; init[stot_init].u = u; init[stot_init].w = s; } bool cmp ( egde a, egde b ) { return a.w > b.w; } int G[100005], flag[100005]; int fa[100005]; int find ( int x ) { if ( fa[x] != x ) return fa[x] = find ( fa[x] ); return x; } int siz[100005]; void unionn ( int x, int y ) { int xx = find ( x ); int yy = find ( y ); fa[xx] = yy; siz[yy] += siz[xx]; } ll ans = 0; void kruskal ( ) { int cnt = 0; for ( RG int i = 1; i <= n; i ++ ) fa[i] = i, siz[i] = 1; sort ( init + 1, init + 1 + stot_init, cmp ); for ( RG int i = 1; i <= stot_init; i ++ ) { if ( cnt >= n ) break; int u = init[i].u, v = init[i].v, uu, vv; if ( ( uu = find ( u ) ) != ( vv = find ( v ) ) ) { ans += 1ll * 2 * siz[uu] * siz[vv] * init[i].w; unionn ( u, v ); } if ( !flag[u] ) flag[u] = 1, cnt ++; if ( !flag[v] ) flag[v] = 1, cnt ++; } } int main ( ) { freopen ( "zoo.in", "r", stdin ); freopen ( "zoo.out", "w", stdout ); scanf ( "%d%d", &n, &m ); for ( int i = 1; i <= n; i ++ ) scanf ( "%d", &G[i] ); for ( RG int i = 1; i <= m; i ++ ) { int u, v; read ( u ); read ( v ); add_init ( u, v, min ( G[u], G[v] ) ); add_init ( v, u, min ( G[u], G[v] ) ); } kruskal ( ); printf ( "%I64d", ans ); return 0; }

题目给出的条件是有一些性质的,每次加入的区间长度总是大于之前的所有区间,所以加入边的时间$i<j$时永远不会出现下图的情况。
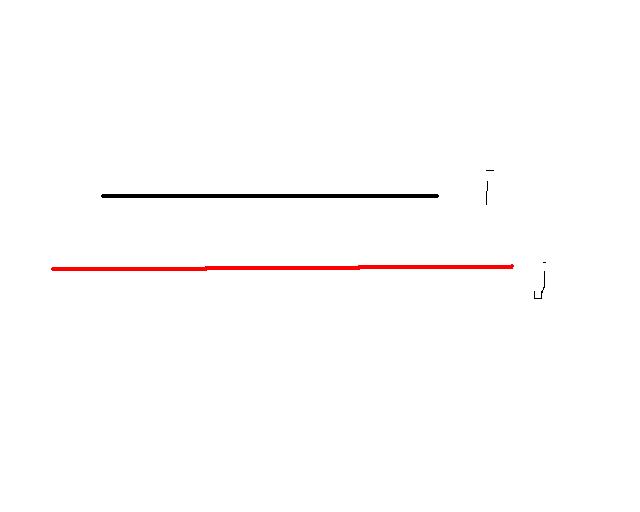
即先加入的边,不可能左端点比后加入的边小,右端点又比后加入的大。所以我们发现,统计当前加入的边的右端点$r$左边【小于等于】有多少个右端点,就是统计了所有在当前边左边的区间,而统计当前边左端点$l$左边【严格小于】的左端点数量,就是统计了所有不被当前边覆盖的区间,相减即可。
用树状数组维护即可。区间需要离散化。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<map> #define ll long long using namespace std; ll a[400005]; int m, del[400005], n, x[400005], qwq[400005], ti; struct TR { ll x, y; int num1, num2, id; } ins[400005]; int lowbit ( int xx ) { return xx & -xx; } int pre1[400005], pre2[400005]; void insert1 ( int xx, int d ) { for ( int i = xx; i <= m; i += lowbit ( i ) ) pre1[i] += d; } void insert2 ( int xx, int d ) { for ( int i = xx; i <= m; i += lowbit ( i ) ) pre2[i] += d; } int query1 ( int xx ) { int ans = 0; for ( int i = xx; i; i -= lowbit ( i ) ) ans += pre1[i]; return ans; } int query2 ( int xx ) { int ans = 0; for ( int i = xx; i; i -= lowbit ( i ) ) ans += pre2[i]; return ans; } int main ( ) { freopen ( "segment.in", "r", stdin ); freopen ( "segment.out", "w", stdout ); int T; scanf ( "%d", &T ); while ( T -- ) { scanf ( "%d", &n ); int ins_t = 0; int tot = 0; memset ( a, 0, sizeof ( a ) ); memset ( ins, 0, sizeof ( ins ) ); memset ( pre1, 0, sizeof ( pre1 ) ); memset ( pre2, 0, sizeof ( pre2 ) ); memset ( del, 0, sizeof ( del ) ); memset ( x, 0, sizeof ( x ) ); for ( int i = 1; i <= n; i ++ ) { int y; scanf ( "%d%d", &x[i], &y ); if ( x[i] == 0 ) { qwq[++ins_t] = i; ins[i].id = i; ins[i].x = y; ins[i].y = y + ins_t; a[++tot] = y; a[++tot] = y + ins_t; } else del[i] = y; } sort ( a + 1, a + 1 + tot ); m = unique ( a + 1, a + 1 + tot ) - a - 1; for ( int i = 1; i <= n; i ++ ) { if ( x[i] == 0 ) { ins[i].num1 = lower_bound ( a + 1, a + 1 + m, ins[i].x ) - a; ins[i].num2 = lower_bound ( a + 1, a + 1 + m, ins[i].y ) - a; } } printf ( "Case #%d: ", ++ti ); for ( int i = 1; i <= n; i ++ ) { if ( x[i] == 0 ) { int wei = query2 ( ins[i].num2 ) - query1 ( ins[i].num1-1 ); printf ( "%d ", wei ); insert1 ( ins[i].num1, 1 ); insert2 ( ins[i].num2, 1 ); } else { insert1 ( ins[qwq[del[i]]].num1, -1 ); insert2 ( ins[qwq[del[i]]].num2, -1 ); } } } return 0; }

非常有意思的一道思路题!!我们可以发现,要使一种方案成立,就是使每行每列都有奇数个-1即可。
题目给出的数据特殊性是$k<max(n,m)$,也就是说,最开始至少有一行或者一列中一个数都没有填。我们不管这行或者这列,考虑其它的行列方案数。我们假设是最后一列一个数都没有填,设前面第$j$列没填的位置有$res[j]$个,第$j$列的方案数实际上是$2^{res[j]-1}$。因为我们发现,我们填每一列的数时,只需要满足填的最后一个数是正确的,其它随便填都可以。所以设前$m-1$列矩形没有填的位置有$res$个,前$m-1$列的总方案数就是$2^{res-(m-1)}$,有$m-1$个数使我们最后填的。而$res=n*(m-1)-k$【最后一列没有填!!】。快速幂即可。
可是又有问题,我们怎么能保证最后一列在前面都填完的情况下一定满足有奇数个-1?下面简单证明一下。假设$m$和$n$都是奇数,整个矩阵中-1的个数就有$奇*奇=奇$个,前$m-1$列有$奇*偶=偶$个,所以最后一列一定有奇数个-1。$m$和$n$都是偶数同理。当$m$和$n$中有一个是奇,一个是偶时,设行数为奇,列数为偶,按每行来看,整个矩阵中一共有$奇*奇=奇$个-1,按每列来看,整个矩阵中一共有$奇*偶=偶$个-1,矛盾。所以此时方案数为0。特判即可。
【注意】当$m$和$n$中有一个为1时需要特判,因为我们假设是一列不填,如果只有一列,res就会减到负数。
#include<iostream> #include<cstdio> #define ll long long using namespace std; int n, m, k, p; ll mi ( ll a, ll b, ll mod ) { ll ans = 1; for ( ; b; b >>= 1, a = a * a % mod ) if ( b & 1 ) ans = ans * a % mod; return ans; } int main ( ) { freopen ( "number.in", "r", stdin ); freopen ( "number.out", "w", stdout ); scanf ( "%d%d", &n, &m ); scanf ( "%d", &k ); ll num = 0; for ( int i = 1; i <= k; i ++ ) { int a, b, c; scanf ( "%d%d%d", &a, &b, &c ); num ++; } ll res; if ( n == 1 || m == 1 ) res = max ( n, m ) - num - 1; else res = 1ll * n * m - n - m - num + 1; scanf ( "%d", &p ); if ( ( m + n ) % 2 ) printf ( "0 " ); else { ll ans = mi ( 2, res, p ); printf ( "%I64d ", ans ); } return 0; }