深度学习课程笔记(四)Gradient Descent 梯度下降算法
2017.10.06
材料来自:http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS17.html
我们知道在神经网络中,我们需要求解的是一个最小化的问题,即:最小化 loss function。

假设我们给定一组初始的参数 $ heta$,那么我们可以算出在当前参数下,这个loss是多少,即表示了这个参数到底有多不好。

然后我们利用上述式子来调整参数,其中梯度可以用▽的形式来表示。我们可以将这个过程可视化出来看看:
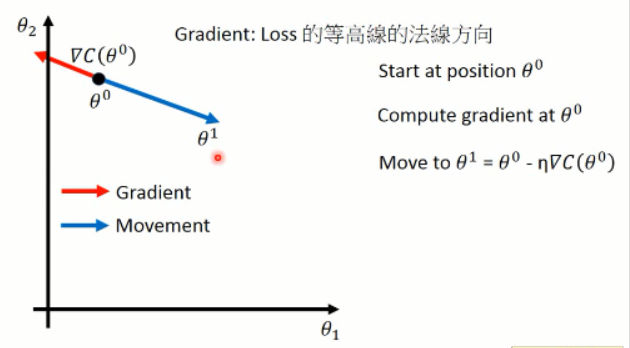
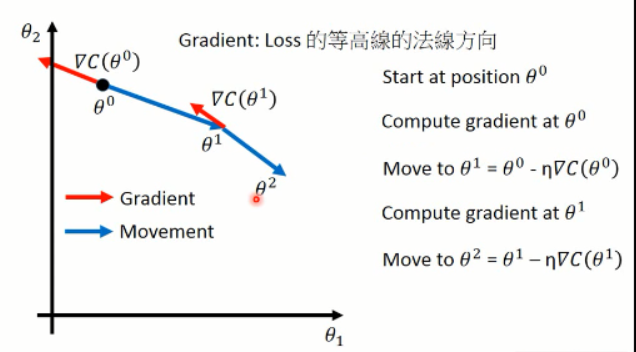
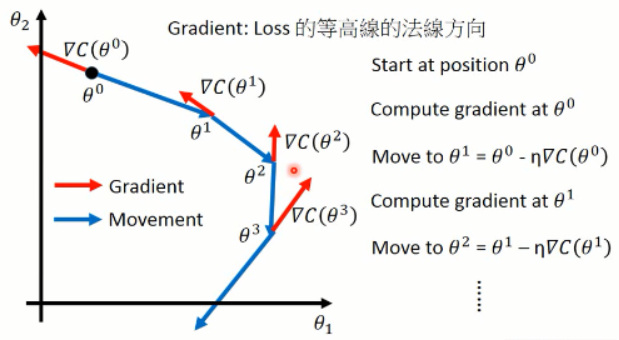
这样子,就算出了每一步当前参数的梯度方向(红色),以及蓝色的调整的方向。这就是梯度下降方法了。
紧接着,李老师讲解了一些梯度下降方法的tips:
1. 调整你的 学习率(learning rate):
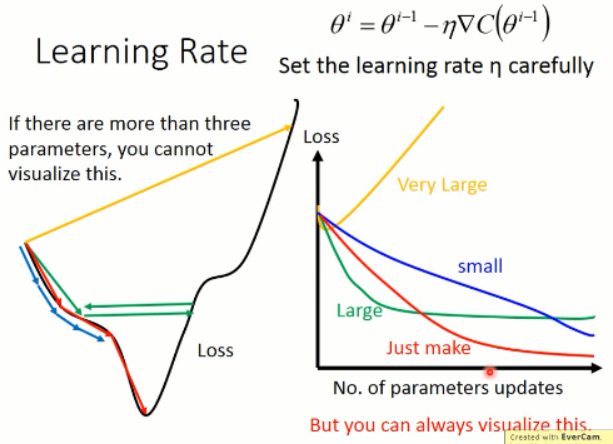
2. 自适应调整的学习率:

我们可以看到,学习率调整的大原则就是:初始的LR 可以调的很大,因为这个时候我们离局部最小值比较远,当时随着学习的进行,我们需要降低学习率,走的步伐要稍微低一点,因为这个时候我们离目的地已经很近了,我们要微调就行了。否则,就可能错过了最好的点。
我们可以将学习率设置为随着迭代次数变化的变量,这样子就可以自适应的调整 LR了。但是,更好的方式,应该是对于不同的参数,都用不同的学习率来进行优化。其中,这类方法中,最直观最简单的,可能就是 Adagrad了。

这里,李老师给了例子来说明,随着学习的进行,权重的更新是如何自适应变化的。
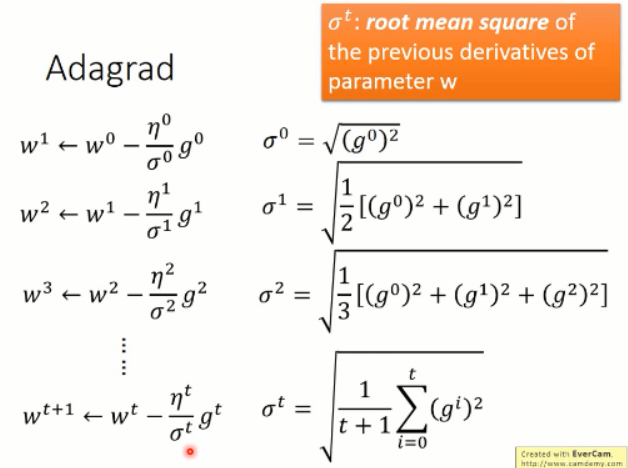
所以,我们将上述式子进一步的化简,可以得到 Adagrad 的参数更新的方程:
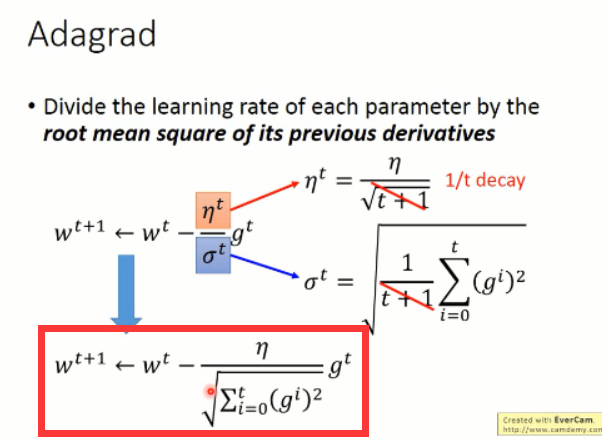
上面就是 Adagrad 方法的全部了,后面李老师对这个更新的方法进行了分析,发现了有如下的看似“不妥当”的东西:当梯度较大的时候,学习的幅度较大,这个没有关系,算是正常;但是,在Adagrad 中,较大的梯度,会导致较大的学习步长,这也没有问题,但是他前面分母当中,较大的梯度,反而使得步长变小了。。。。这又该怎么解释呢?
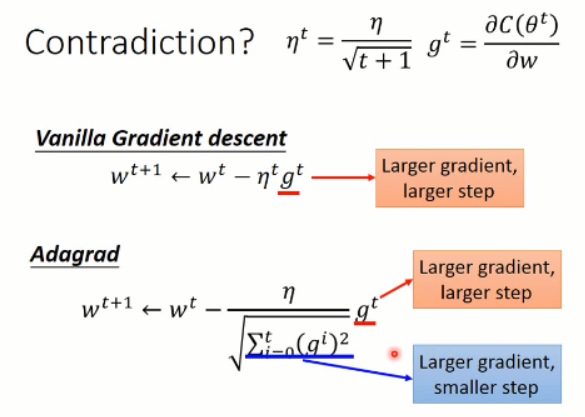
有一种直观的解释是,这里的 Adagrad 描绘了梯度变化中,反差的情况:
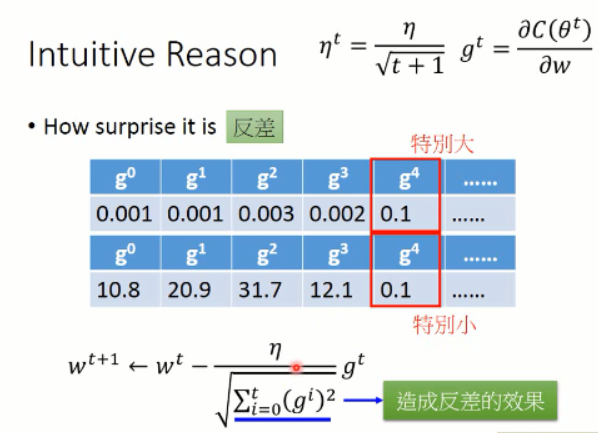
此外,还有另外一种比较正式的解释:
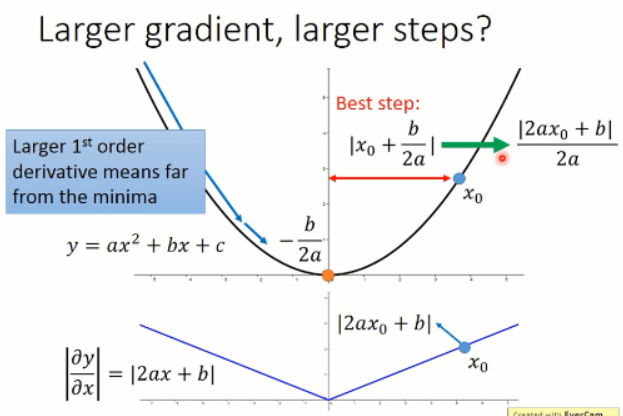
假设我们从 x0 开始出发,我们到最小值处的最优的步长应该是上图中 Best step 所描绘的那样子,而这个值恰好是目标函数微分后的函数在 x0 处的微分值。所以,较好的步长设置应该是 与微分值成正比的一个数字。这是在只考虑一个参数的时候,才成立的。
如果有多个参数,同时影响这个函数的话,情况就很不一样了。此时, gradient 的值越大,那么离局部最小就一定越远,这句话就要打一个问号了。这句话变的不一定成立了。
我们考虑两个参数的情况,w1 and w2 构成下面这样子的梯度情况:
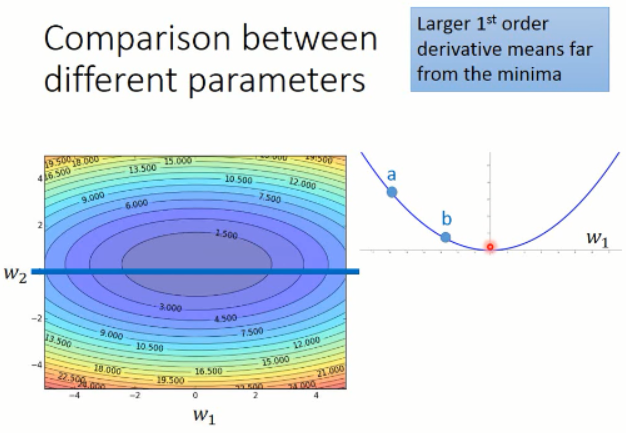
我们在只考虑参数 w1 的情况下,我们可以发现,在 a 点的微分值 是比 b 点的微分值要大的。同时,只对于 w2 来说,也是这样子的。
但是,当跨参数比较的时候,这个结论就不一定成立了。我们来看看下面的这个例子:
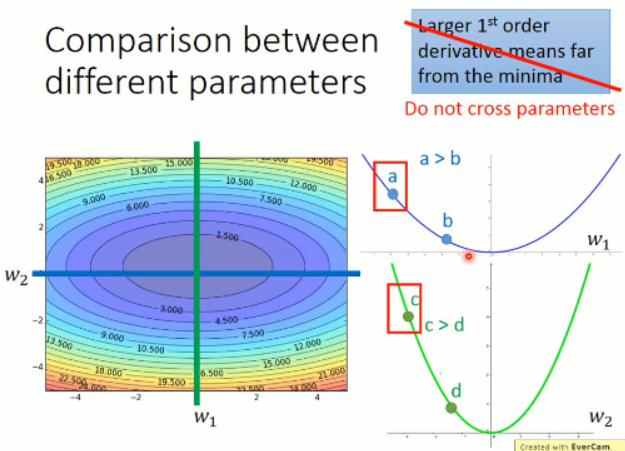
我们来比较下 a 点 和 c点的情况,虽然 c点的梯度比 a点的梯度要大,但是实际上,c点离局部最小值的距离是更近的。所以,梯度大,并不一定离得就远。。。。
比较合理的是,引入二次微分,我们发现最优步长中分母项是 2a,这个 2a 就是那个函数求二阶导数得到的。所以,当前情况下,最好的步长应该是与一次微分成正比,与二次微分成反比的。如下图所示:
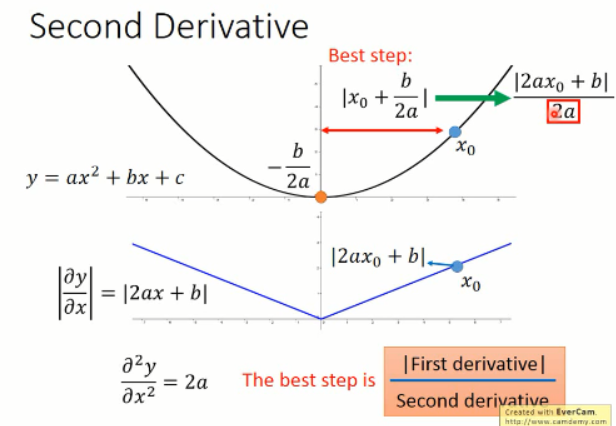
那么,我们再来看看梯度变化的展示图:
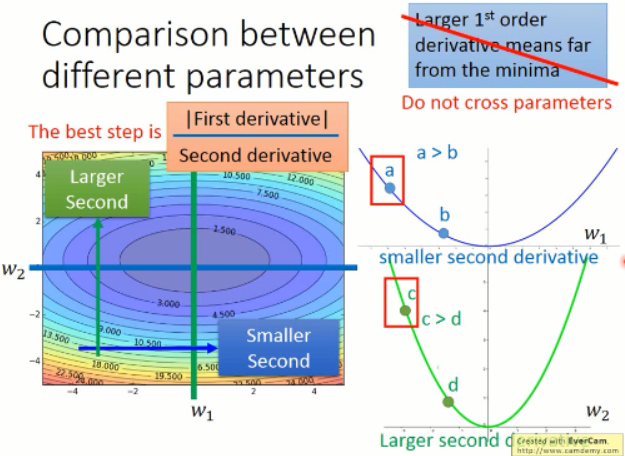
我们可以看到,在 w2 方向上的二阶导数变化是比较小的,而w1方向上的变化是比较大的。我们同时考虑一阶导数和二阶导数,才能真正的反应,某一点,离原点的距离。再来看,a 和 c 点,分子分母都相对的比较小,比较大,就很难看出到底是哪个比较近了。所以,这个时候需要带入,算一算,才知道咯?!!那么,这个现象和 Adagrad 到底有什么关系呢?
神奇的是,Adagrad 就已经在模拟这个比值了:
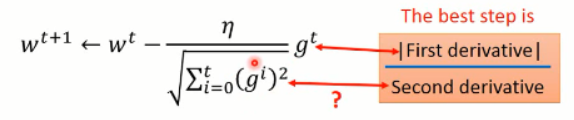
其中的 gt 就是一阶导数,分母虽然不是显示的求解的二阶导数,但是已经是在模拟这个过程了。因为求解二阶导数是需要额外耗费时间的,所以,我们在不增加额外计算量的情况下,可以估计其二阶导数,何乐而不为呢?
假设我们这里有两个函数,其一阶导数分别为:
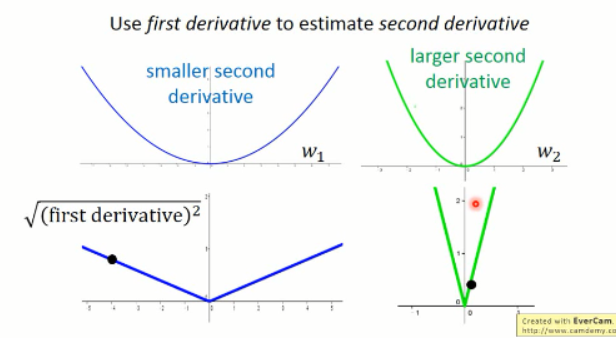
如果我们只采样一个点,我们是很难根据一阶导数估计其二阶导数的,但是我们可以采样很多点啊。。对不对。。。Ok. 如果有很多点,那么:
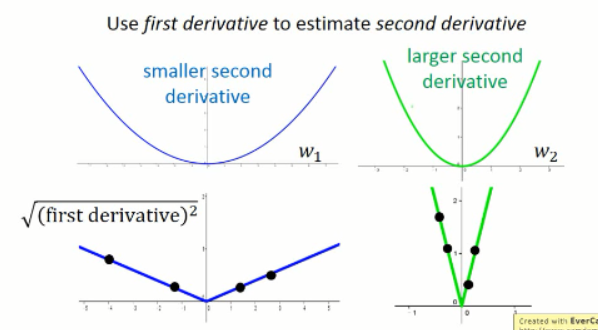
我们有了这么多采样的点,那么,我们可以看出在比较宽的峡谷中,我们得到的梯度是比较小的,而在比较窄的峡谷中,我们得到的梯度是比较大的。我们将这些点都平均起来来看,那么,就可以大致估计出二阶导数的大小了。
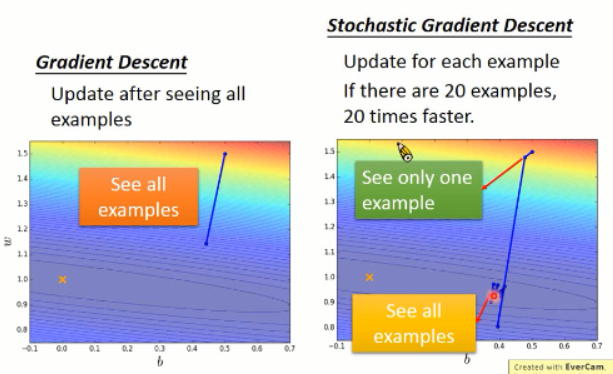
关于 Adagrad 大概就是这样子。接下来 我们来看看什么是随机梯度下降(stochastic gradent descent):
先说说这个方法的好处吧,恩,就是: make your training faster ...

我们知道,总的 Loss function 是所有样本的 loss 加和,得到的。而梯度下降就是利用所有的 loss 结果来求解。而 SGD 是仅仅对 一个样本进行 loss 的求解,并且更新的时候,只考虑一个样本。也就是说,来一个样本,我就算一次,更新一次,而跟其他的样本没有交集。
接下来就是第三个 tip 了: Feature Scaling
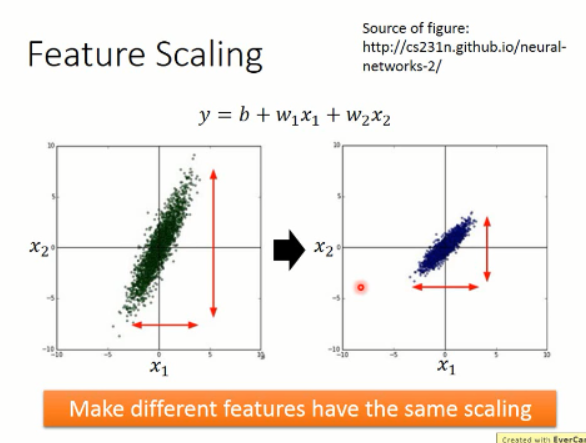
那么,这么做有什么好处呢?加入输入的 feature 中,两个样本 x1 and x2 之间的差距较大,那么,就会导致出现左侧那种椭圆形的等高线的情况,而右侧这种比较一致的 feature 输入,会得到一组比较靠近圆形的等高线。这有什么区别吗?
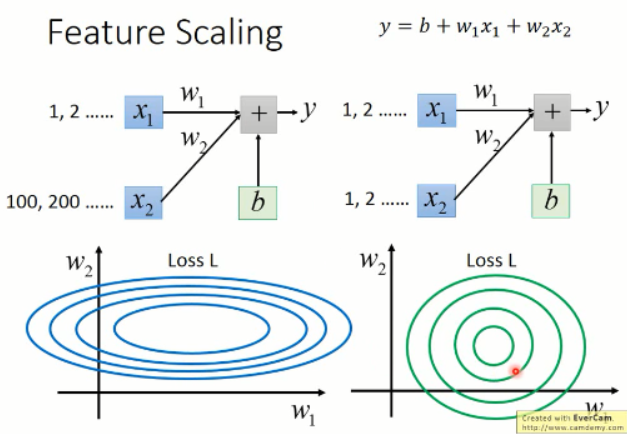
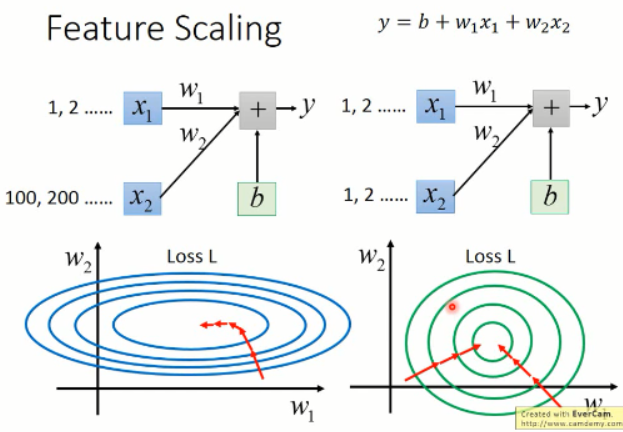
我们继续来看,我们是要用梯度下降来去优化参数,那么我们在左侧椭圆形等高线情况下,就必须得用 Adagrad 这样的优化方法来做了,因为他每一处的梯度都是方向不同的,她是沿着红色曲线的方向进行优化的。
而圆形的这种变化趋势,我们发现,这种可以直接沿着直线的方向,直接就可以优化到圆形的中心点。这实际上是非常平滑的,而且速度上可能有优势。优化起来,比较平滑。
那么,既然有这么多好处,我们该怎么做这个 feature scaling 呢?
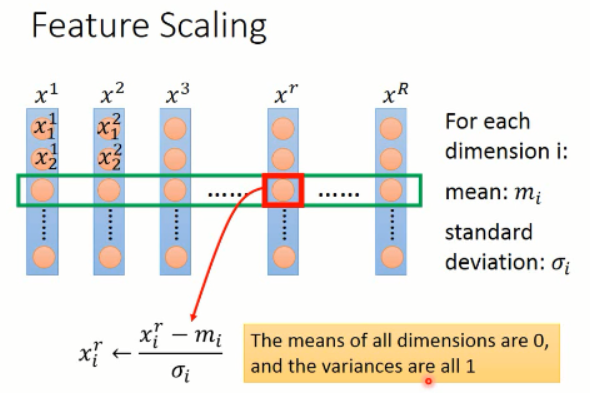
一种比较简单的处理方法就是:对 feature 的每一个维度,我们求出其均值和标准差,然后对每一个 value,减去均值然后再除以标准差,就可以得到修改后的 feature value了。
那么,梯度下降方法能work 的原因是什么呢?

我们首先来看一个例子:
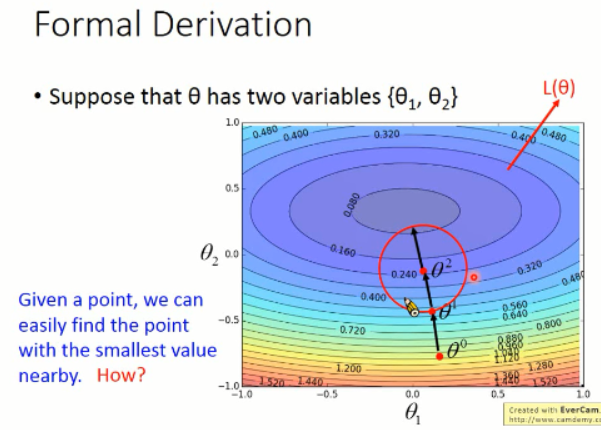
那么,现在我们的问题就是:给定一个点,我们怎么找到其附近区域内的最小的那个点呢???我们先来看看泰勒级数的问题:

这里给了一个例子:
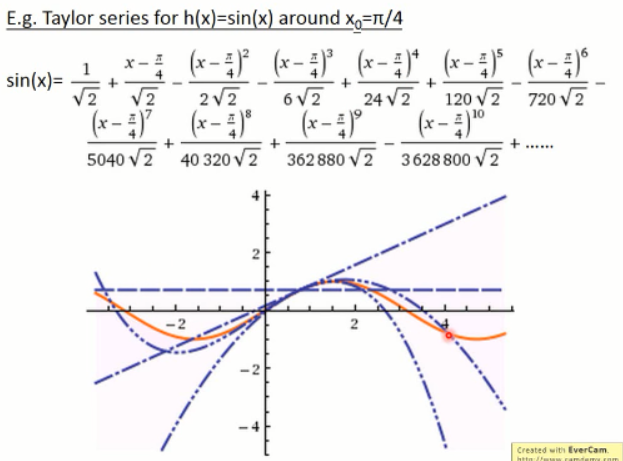
上面提到的是单个变量的泰勒展开式,我们来看看多变量的情况:

那么,我们再次回到那个 formal Derivation 的问题:

我们考虑在圆形内部的情况:
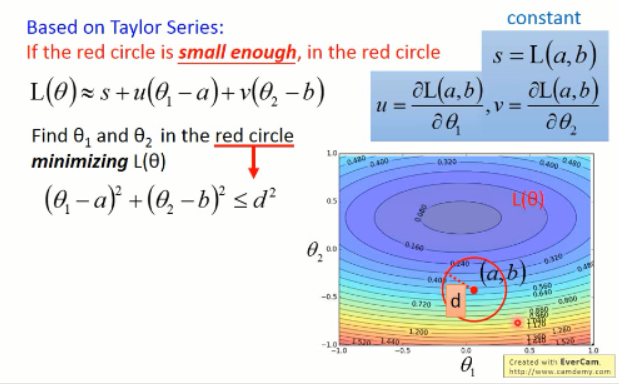

我们所要找的最优的 theta 1 and theta 2 就是和 (u, v)反方向的,并且长度是圆形的半径那样子的。

我们把 u 和 v 带进去之后,就发现,这原来就是 gradient descent:

梯度下降的缺点:
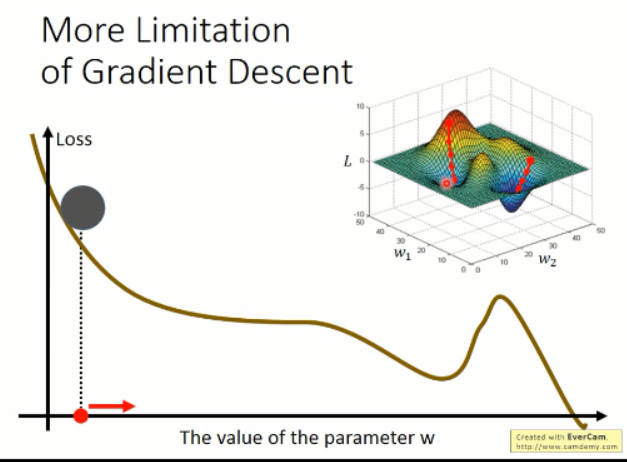
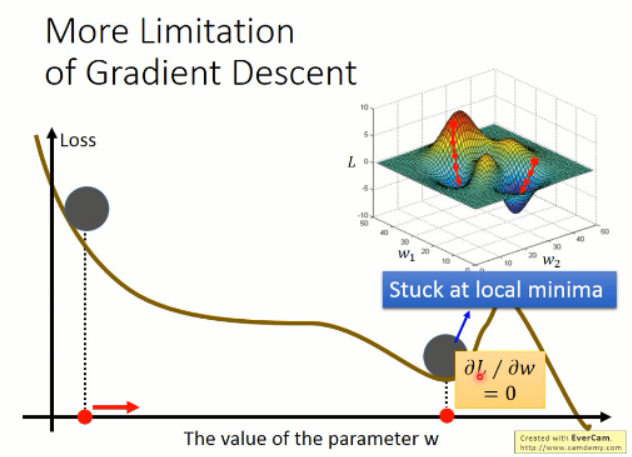
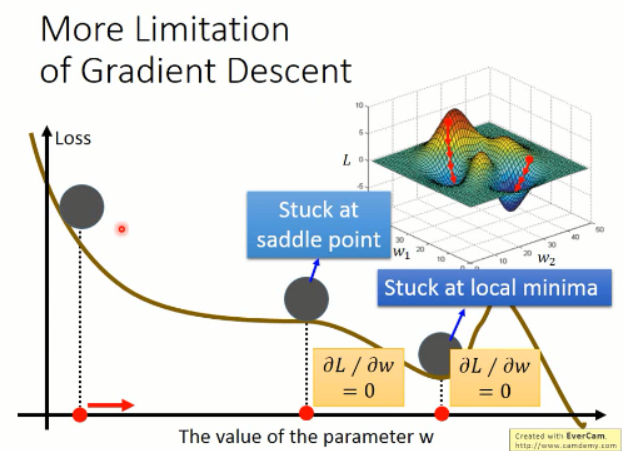
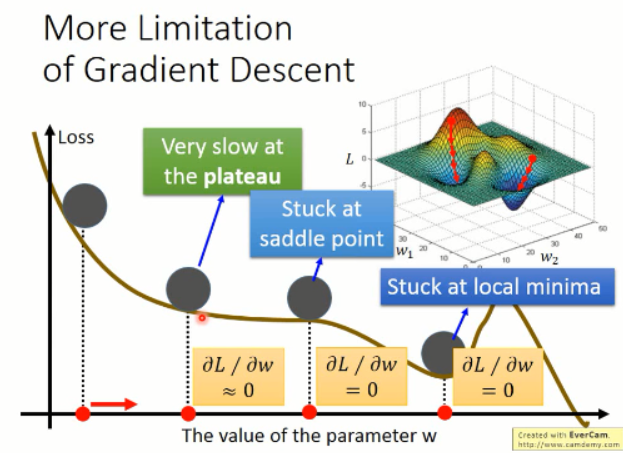
根据以上的图像,我们知道有几个缺点是比较明显的:
1. 容易卡在局部最小值;而不是全局最小;
2. 容易卡在 saddle point;
3. 容易在比较平坦的地方,让你觉得,哦,loss 接近于 0 了,应该训练的差不多了。。。
4. 。。。