L1正则和L2正则的区别详解

正则化本身是一种参数范数惩罚，即权重衰减。

L2参数正则化

L2参数正则化策略通过向目标函数添加一个正则项 $wVert_{2}^{2})$ ，来使权重更加接近原点。其他学术圈称L2为岭回归或者Tikhonov正则。
在这里插入图片描述
下图中 $\tilde{w}$ 即为增加L2正则项之后所求的参数集， $w^*$ 则是为加正则项所要求的参数集，进行了特征分解。

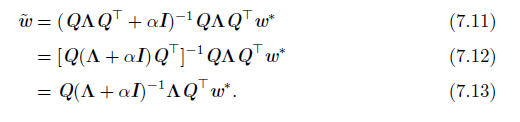
L2正则化能让学习算法"感知"到具有较高方差的输入x，因此与输出目标的协方差较小(相对增加方差)的特征的权重将会收缩(证明详见Deep Learning Chapter 7.1.1)。

L1参数正则化

形式化地，L1正则化定义为：
$Vert_1 = sum_i{|w_i|}$

在这里插入图片描述
相对于L2正则化，L1正则化会产生更稀疏的解。这里的稀疏性是指最优值中一些参数为0，即0更多的参数集。由式子7.23可知， $|w_i^*| < frac{alpha}{H_{i,j}}$ ，参数集的i维就被指定成了0，而观察L2正则的式子7.13，L2正则只是放缩了原参数集的大小，并不能使其为零。

由于L1正则化导出的稀疏性质已经被广泛的用于特征选择机制。特征选择从可用的特征子集中选择有意义的特征，从而化简机器学习问题。著名的LASSO模型将L1惩罚和线性模型相组合，并使用最小二乘代价函数。如果L1惩罚是的部分子集的权重为0，则表示相应的特征可以被安全的忽略。

L2正则化相当于是高斯先验的MAP贝叶斯推断；L1正则化等价于通过MAP贝叶斯推断最大化对数先验项。

或者从分布的角度而言：

L1范数符合拉普拉斯分布，是不完全可微的。表现在图像上会有很多角出现。这些角和目标函数的接触机会远大于其他部分。就会造成最优值出现在坐标轴上，因此就会导致某一维的权重为0 ，产生稀疏权重矩阵，进而防止过拟合。

L2范数符合高斯分布，是完全可微的。和L1相比，图像上的棱角被圆滑了很多。一般最优值不会在坐标轴上出现。在最小化正则项时，可以是参数不断趋向于0，最后活的很小的参数。

画图表示：
L2正则：
在在这里插入图片描述
在L2正则下，w从P1向P2移动，w减小，L2正则项使参数变小。

L1正则：
在这里插入图片描述
在L1正则下，w向w2轴移动，到达w2轴即变为零，因为容易稀疏化。