前言
含参数的二次不等式的求解是高中学生的难点,涉及到代数的内涵。
数字系数
分析:(xin [1,3]);
字母系数
- 含参数的二次不等式,一动根一定根
- (含参数的二次不等式,两动根)
分析:将原不等式等价转化为((x-a)(x+cfrac{a}{2})<0),
令((x-a)(x+cfrac{a}{2})=0),
则方程的两个根为(x=-cfrac{a}{2})和(x=a),
下来根据这两个动根的大小分类讨论

当(-cfrac{a}{2}<a)时,即(a>0)时,不等式的解集为((-cfrac{a}{2},a));
当(-cfrac{a}{2}=a)时,即(a=0)时,不等式的解集为(varnothing);
当(-cfrac{a}{2}>a)时,即(a<0)时,不等式的解集为((a,-cfrac{a}{2}));
综上,略。
分析:将原不等式等价转化为((x-a^2)(x-a)leq 0),
其对应方程的两个根为(x=a^2)和(x=a),分类讨论如下:
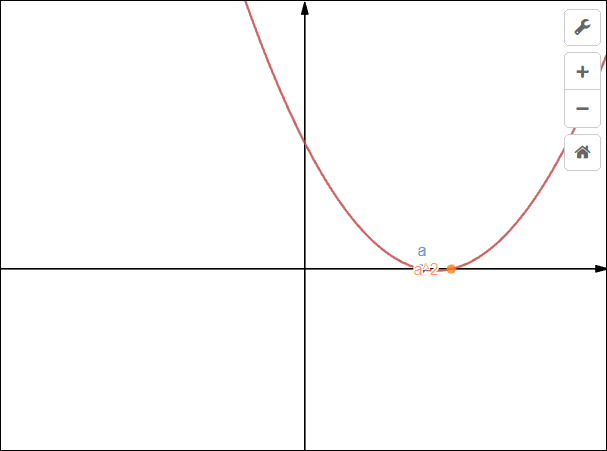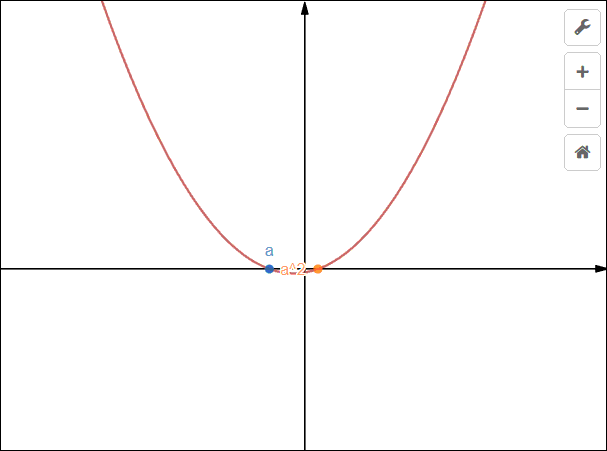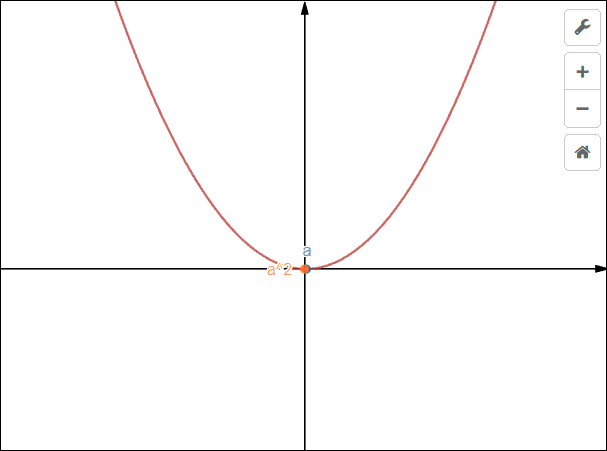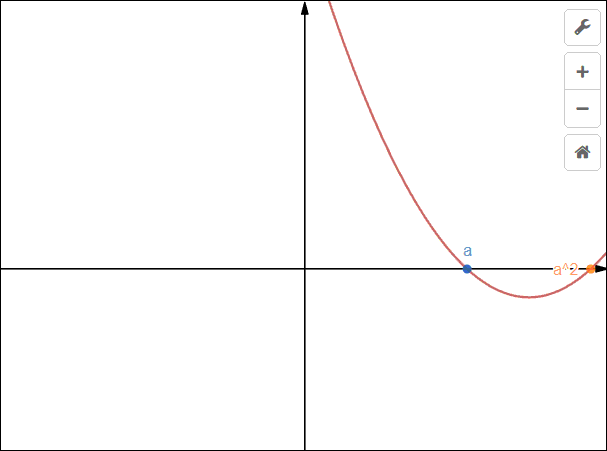
(1^{circ}) 当(a^2>a),即(a<0)或(a>1)时,解集为([a,a^2]);
(2^{circ}) 当(a^2=a),即(a=0)或(a=1)时,解集为({0,1});
(3^{circ}) 当(a^2<a),即(0<a<1)时,解集为([a^2,a]);
综上所述:
当(a<0)或(a>1)时,解集为([a,a^2]);
当(a=0)或(a=1)时,解集为({0,1});
当(0<a<1)时,解集为([a^2,a]);
分析:当(a=1)时,原不等式为(1<0),故解集为(varnothing);
当(a eq 1)时,由于(a^2+1>2a),故解集为((2a,a^2+1));
分析:若(a=0)时,原不等式等价于(-x+1<0),即(x>1);
若(a<0)时,原不等式等价于((x-cfrac{1}{a})(x-1)>0),解得(x<cfrac{1}{a})或(x>1);
若(a>0)时,原不等式等价于((x-cfrac{1}{a})(x-1)<0),
当(cfrac{1}{a}=1)时,即(a=1)时,不等式无解;
当(cfrac{1}{a}<1)时,即(a>1)时,不等式解集为({xmid cfrac{1}{a}<x<1});
当(cfrac{1}{a}>1)时,即(0<a<1)时,不等式解集为({xmid 1<x< cfrac{1}{a}});
综上所述,
当(a<0)时,不等式解集为({xmid x<cfrac{1}{a})或(x>1});
当(a=0)时,不等式解集为({xmid x>1});
当(0<a<1)时,不等式解集为({xmid 1<x< cfrac{1}{a}});
当(a=1)时,不等式解集为(varnothing);
当(a>1)时,不等式解集为({xmid cfrac{1}{a}<x<1});
因式分解
实际高三数学教学和考试中的相关习题常常是这样的,理解掌握。
①(x^2-5sqrt{2}x+8ge 0),即((x-sqrt{2})(x-4sqrt{2})ge 0);
②(x^2-(2m+1)x+m^2+m-2leq 0),即([x-(m+2)][x-(m-1)]leq 0);
③(x^2-3mx+(m-1)(2m+1)ge 0);即([x-(m-1)][x-(2m+1)]ge 0);
④(x^2-(a+a^2)x+a^3leq 0),即((x-a)(x-a^2)leq 0);
⑤(x^2-(a+1)x+aleq 0),即((x-1)(x-a)leq 0);
⑥(x^2-(2a+1)x+a(a+1)leq 0);即((x-a)[x-(a+1)]leq 0);
⑦(cfrac{x-2a}{x-(a^2+1)}<0(a eq 1));即((x-2a)[x-(a^2+1)]<0),解集为((2a,a^2+1));
⑧(x^2+(m+4)x+m+3<0),即((x+1)[x+(m+3)]<0);
转化划归
【分析】利用导数转化为求解含有参数a的不等式,给导函数的分子配方就能找到分类讨论的标准。
【解答】导数法研究单调性,先求出定义域((-1,+infty)),
(f'(x)=x+cfrac{a}{x+1})(=cfrac{x(x+1)+a}{x+1})(=cfrac{x^2+x+a}{x+1})(=cfrac{(x+cfrac{1}{2})^2+a-cfrac{1}{4}}{x+1}),
①当(a≥cfrac{1}{4})时,(f'(x)≥0)恒成立,且当(a=cfrac{1}{4})时仅仅在(x=-cfrac{1}{2})处取到等号,
故函数(f(x))在((-1,+∞))上单调递增;
②当(a<cfrac{1}{4})时,令(x^2+x+a=0),得到(x=cfrac{-1±sqrt{1-4a}}{2}),
接下来将其中的小根和-1作比较,
当(-1<cfrac{-1-sqrt{1-4a}}{2})时,即(0<a<cfrac{1}{4})时,
(xin (-1,cfrac{-1-sqrt{1-4a}}{2}))时,(f'(x)>0),(f(x))单调递增,
(xin(cfrac{-1-sqrt{1-4a}}{2},cfrac{-1+sqrt{1-4a}}{2}))时,(f'(x)<0),(f(x))单调递减,
(xin(cfrac{-1+sqrt{1-4a}}{2},+infty))时,(f'(x)>0),(f(x))单调递增,
当(-1=cfrac{-1-sqrt{1-4a}}{2})时,即(a=0)时,(xin (-1,cfrac{-1+sqrt{1-4a}}{2}))时,(f'(x)<0),(f(x))单调递减,(xin(cfrac{-1+sqrt{1-4a}}{2},+infty))时,(f'(x)>0),(f(x))单调递增,
当(-1>cfrac{-1-sqrt{1-4a}}{2})时,即(a<0)时,(xin(-1,cfrac{-1+sqrt{1-4a}}{2}))时,(f'(x)<0),(f(x))单调递减,(xin(cfrac{-1+sqrt{1-4a}}{2},+infty))时,(f'(x)>0),(f(x))单调递增,
综上所述,当(a≥cfrac{1}{4})时,函数(f(x))的单调递增区间为((-1,+∞)),无单调递减区间;
当(0<a<cfrac{1}{4})时,单调递增区间为((-1,cfrac{-1-sqrt{1-4a}}{2}))和((cfrac{-1+sqrt{1-4a}}{2},+infty)),
单调递减区间为((cfrac{-1-sqrt{1-4a}}{2},cfrac{-1+sqrt{1-4a}}{2}));
当(a≤0)时,单调递减区间为((-1,cfrac{-1+sqrt{1-4a}}{2})),单调递增区间为((cfrac{-1+sqrt{1-4a}}{2},+infty));
分析:函数(f(x))的定义域为((-infty,+infty)),(f'(x)=ax^2-(a+1)x+1=a(x-cfrac{1}{a})(x-1)),
当(cfrac{1}{a}=1)时,即(a=1)时,(f'(x)geqslant 0)恒成立,则在((-infty,+infty))单调递增;
当(cfrac{1}{a}<1)时,即(a>1)时,
当(xin (-infty,cfrac{1}{a}))时,(f'(x)>0),(f(x))单调递增;当(xin (cfrac{1}{a},1))时,(f'(x)<0),(f(x))单调递减;当(xin (1,+infty))时,(f'(x)>0),(f(x))单调递增;
当(cfrac{1}{a}>1)时,即(0<a<1)时,
当(xin (-infty,1))时,(f'(x)>0),(f(x))单调递增;当(xin (1,cfrac{1}{a}))时,(f'(x)<0),(f(x))单调递减;当(xin (cfrac{1}{a},+infty))时,(f'(x)>0),(f(x))单调递增;
综上所述,
当(0<a<1)时,函数的单调递增区间为((-infty,1))和((cfrac{1}{a},+infty)),单调递减区间为((1,cfrac{1}{a}));
当(a=1)时,函数的单调递增区间为((-infty,+infty));
当(a>1)时,函数的单调递增区间为((-infty,cfrac{1}{a}))和((1,+infty)),单调递减区间为((cfrac{1}{a},1));