前言
当我们借助导数工具研究函数的单调性、极值、最值时,难在解导函数不等式,此时如果能灵活而恰当的使用函数的图像时,就可以轻松的判断导函数的正负了。
使用步骤
- 当题目给定函数[数字系数,不含有参数]后,用导数法求数字系数的函数极值的步骤:
①确定函数的定义域;
②求导数(f'(x));
③解方程(f'(x)=0),求出在函数定义域内的所有根;
④解导函数不等式(f'(x)>0)或(f'(x)<0),此时若不等式不好解,可以借助导函数的图像,通过解读图像得到解集;
⑤列表检验(f'(x))在(f'(x)=0)的根(x_0)左右两侧值的符号.
⑥由表格得到极值和极值点;
补充:当函数中含有参数时,用导数法求字母系数的函数极值的步骤:
需要分类讨论;每一种情形都对应上述的求解步骤;
案例解析
(1)若曲线 (y=f(x)) 在点 ((1, f(1))) 处的切线与直线 (y=1) 平行, 求 (a) 的值;
解:因为(f(x)=cfrac{ax^{2}+(4a-2)x+4a-6}{{e}^{x}}),
所以 (f'(x)=cfrac{(2ax+4a-2){e}^{x}-left[ax^{2}+(4a-2)x+4a-6 ight]{e}^{x}}{{e}^{2x}})
(=cfrac{-ax^2-(2a-2)x+4}{e^x}=-cfrac{ax^2+(2a-2)x-4}{e^x})
(=-cfrac{(ax-2)(x+2)}{{e}^{x}})〖反思〗:求导的实战中,求导、通分、因式分解等运算往往都是连在一起的。那么为什么要通分呢,由于我们关注导函数的正负,通分后就不需要再关注分母(x),分母为正,对函数模型做减法,将变量集中到分子上,只需要关注分子就行了;为什么要因式分解呢,我们是为了便于看出来两个零点,便于下一步分类讨论; .
由题设知 (f'(1)=cfrac{-3(a-2)}{e}=0), 解得 (a=2) .
又由于此时 (f(1)=cfrac{10}{e} eq 1)题目告诉函数在点 ((1,f(1))) 处的切线与直线 (y=1) 平行,故需要验证,以保证不能重合;, 所以 (a) 的值为 (2) .
(2)若 (f(x)) 在 (x=-2) 处取得极大值, 求 (a) 的取值范围. [重难点]
解:由上可知,(f'(x)=-cfrac{(ax-2)(x+2)}{{e}^{x}})到此,我们该如何思考呢,当将着眼点只关注(y)(=)(-)((ax-2))(cdot)((x+2))时,发现其为仿二次函数,故需要针对二次项系数分类讨论,因为只有分类讨论才能说清楚导函数的正负;如何分类呢?先分类为(a=0)[一次函数],再分类为(a>0)和(a<0)[二次函数],定义域为(R),
① 当(a=0)时,分子函数简化为(y=2(x+2)),
故当(xin (-infty,-2))时,(f'(x)<0),(f(x))单调递减甚至可以借助更简化的函数(y=x+2)的图像来判断导函数的正负,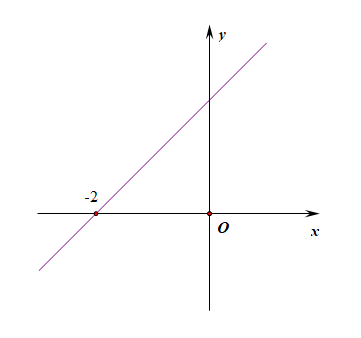 其中(x)轴上方的函数值为正,下方为负;,
其中(x)轴上方的函数值为正,下方为负;,
(xin (-2,+infty))时,(f'(x)>0),(f(x))单调递增,
故函数在(x=-2)处取到极小值,不符合题意,舍去.
② 当(a>0)时,分子函数化简为(y=-a(x-cfrac{2}{a})(x+2))此时函数为二次函数,图像为开口向下的抛物线,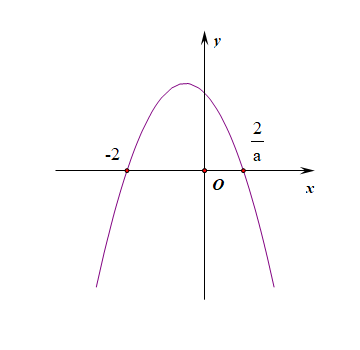 ,且(cfrac{2}{a}>-2),
,且(cfrac{2}{a}>-2),
当(xin (-infty,-2))时,(f'(x)<0),(f(x))单调递减,
(xin (-2,cfrac{2}{a}))时,(f'(x)>0),(f(x))单调递增,
(xin (cfrac{2}{a},+infty))时,(f'(x)<0),(f(x))单调递减,
故函数在(x=-2)处取到极小值,不符合题意,舍去.
③当(-1<a<0)时这个分类标准是如何来的?当(a<0)时,二次函数的两个零点就有了相等的可能,让两个零点(cfrac{2}{a})(=)(-2),解得分界点为(a)(=)(-1),然后通过解(cfrac{2}{a})(<)(-2)得到(-1)(<)(a)(<0),解(cfrac{2}{a})(>)(-2)得到(a)(<)(-1),故接下来应该分类讨论以下三种情形:(-1)(<)(a)(<)(0),(a)(=)(-1),(a)(<)(-1),分子函数化简为(y=-a(x-cfrac{2}{a})(x+2))此时函数为二次函数,图像为开口向上的抛物线, ,且(cfrac{2}{a}<-2),
,且(cfrac{2}{a}<-2),
当(xin (-infty,cfrac{2}{a}))时,(f'(x)>0),(f(x))单调递增,
(xin (cfrac{2}{a},-2))时,(f'(x)<0),(f(x))单调递减,
(xin (2,+infty))时,(f'(x)>0),(f(x))单调递增,
故函数在(x=-2)处取到极小值,不符合题意,舍去.
④当(a=-1)时,分子函数化简为(y=(x+2)^2)此时函数为二次函数,图像为开口向上的抛物线,图像和(x)轴相切,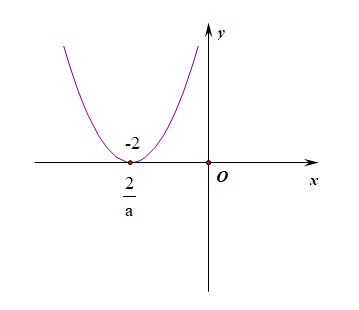 ,且(cfrac{2}{a}=-2),
,且(cfrac{2}{a}=-2),
当(xin (-infty,+infty))时,(f'(x)geqslant0),(f(x))单调递增,
此时函数没有极值,不符合题意,舍去.
⑤当(a<-1)时,分子函数化简为(y=-a(x-cfrac{2}{a})(x+2))此时更简单的函数模型(y=(x-cfrac{2}{a})(x+2))为二次函数,图像为开口向上的抛物线, ,且(cfrac{2}{a}>-2),
,且(cfrac{2}{a}>-2),
当(xin (-infty,-2))时,(f'(x)<0),(f(x))单调递增,
(xin (-2,cfrac{2}{a}))时,(f'(x)>0),(f(x))单调递减,
(xin (cfrac{2}{a},+infty))时,(f'(x)<0),(f(x))单调递增,
故函数在(x=-2)处取到极大值,符合题意,
综上所述,(a)的取值范围为((-infty,-1)) .
〔解后反思〕:①本题目的难点之一,就是分类讨论的原因和分类讨论的标准的确定;
②我们能体会到,当恰当使用了图像后,导函数的正负判断就变得非常容易,学生也可以自己轻松的写出来。
③在使用图像时我们使用了减法,本来应该是做函数(f'(x)=-cfrac{(ax-2)(x+2)}{e^x})的完整图像,可是我们手工做不出,鉴于(e^x>0),故我们只要做出(y=-(ax-2)(x+2))的图像,就可以判断(f'(x))的正负,从而就能判断原函数的单调性了。