前言
极值点偏移问题,可以说是高中数学学习中最难的数学问题之一。
含义与判定
极值点偏移的含义:
若单峰函数 (f(x)) 的极值点为(x_0),则极值点的偏移问题的图示及函数值的大小关系如下表所示.
| 偏移类型 | 极值点(x_0)偏移情况 | 函数值的大小关系 | 示意图像 |
|---|---|---|---|
| 极值点 不偏移 |
(x_0=cfrac{x_1+x_2}{2}) | (f(x_1)=f(2x_0-x_2)) |  |
| 极值点 偏移 |
极值点左移; (x_0<cfrac{x_1+x_2}{2}) |
峰口向上; (f(x_1)>f(2x_0-x_2)) |
 |
| 极值点 偏移 |
极值点左移; (x_0<cfrac{x_1+x_2}{2}) |
峰口向下; (f(x_1)>f(2x_0-x_2)) |
 |
| 极值点 偏移 |
极值点右移; (x_0>cfrac{x_1+x_2}{2}) |
峰口向上; (f(x_1)>f(2x_0-x_2)) |
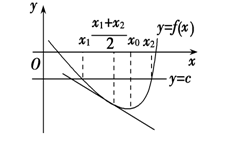 |
| 极值点 偏移 |
极值点右移; (x_0>cfrac{x_1+x_2}{2}) |
峰口向下; (f(x_1)<f(2x_0-x_2)) |
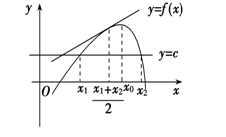 |
题型及解法
函数极值点偏移问题的题型及解法
(1)极值点偏移问题的题设一般有以下四种形式:
①若函数(f(x)) 在定义域上存在两个零点(x_1),(x_2)((x_1 eq x2)),求证:(x_1+x_2>2x_0)((x_0)为函数(f(x))的极值点);
②若函数(f(x)) 在定义域上存在(x_1),(x_2)((x_1 eq x2))满足(f(x_1)=f(x_2)),求证:(x_1+x_2>2x_0)((x_0)为函数(f(x))的极值点);
③若函数(f(x))存在两个零点(x_1),(x_2)((x_1 eq x_2)),令(x_0=cfrac{x_1+x_2}{2}),求证:(f'(x_0)>0);
④若在函数(f(x)) 的定义域上存在(x_1),(x_2)((x_1 eq x_2))满足(f(x_1)=f(x_2)),令(x_0=cfrac{x_1+x_2}{2}),求证:(f'(x_0)>0);
典例剖析
【法一】:[抓极值点构造函数]由题意,函数(f(x))有两个零点(x_1),(x_2)((x_1)( eq)(x_2)),即(f(x_1)=f(x_2)=0),
易知(ln x_1),(ln x_2)是方程(x=acdot e^x)的两根。设(t_1=ln x_1),(t_2=ln x_2),
设(g(x)=xcdot e^{-x}),则(g(t_1)=g(t_2)),
从而(x_1x_2>e^2) (Leftrightarrow) (ln x_{_1}+ln x_2>2) (Leftrightarrow) (t_1+t_2>2).
以下证明:(t_1+t_2>2).
(g'(x)=(1-x)e^{-x}),易得(g(x))在((-infty,1))上单调递增,在((1,+infty))上单调递减,
所以函数(g(x))在(x=1)处取得极大值(g(1)=cfrac{1}{e}).
当(x ightarrow -infty)时,(g(x) ightarrow -infty);
当(x ightarrow +infty)时,(g(x) ightarrow 0) 且(g(x)>0);
由(g(t_1)=g(t_2)),(t_1 eq t_2),不妨设(t_1<t_2),
作出函数(g(x))的图像,如图所示,由图知必有(0<t_1<1<t_2),
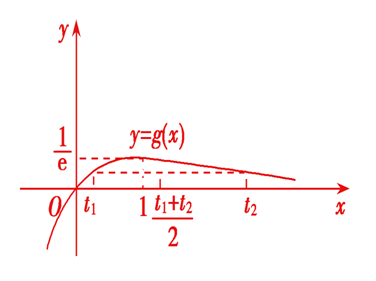
令(F(x)=g(1+x)- g(1-x)),(x∈(0,1]),
则(F'(x)=g'(1+x)-g'(1-x))(=cfrac{x}{e^{x+1}}(e^{2x}-1)>0),所以(F(x))在((0,1])上单调递增,
所以(F(x)>F(0)=0)对任意的(x∈(0,1])恒成立,即(g(1+x)>g(1-x))对任意的(x∈(0,1])恒成立。
由(0<t_1<1<t_2),得(1-t_1∈(0,1]),
所以(g(1+(1-t_1))=g(2-t_1)>g(1-(1-t_1))=g(t_1)=g(t_2)),
即(g(2-t_1)>g(t_2)),又(2-t_1),(t_2∈(1,+∞)),
且(g(x))在((1,+∞))上单调递减,所以(2-t_1<t_2),
即(t_1+t_2>2),故(x_1x_2>e^2).
[法1总结]:上述解题过程就是解决极值点偏移问题的最基本的方法,共有四个解题要点:
(1)求函数(g(x))的极值点(x_0),
(2)构造函数(F(x)=g(x_0+x)-g(x_0-x)),
(3)确定函数(F(x))的单调性,
(4)结合(F(0)=0),确定(g(x_0+x))与(g(x_0-x))的大小关系.
其口诀为:极值偏离对称轴,构造函数觅行踪,四个步骤环相扣,两次单调紧跟随.
【法二】:[巧抓“根差”—(s=Delta t=t_2-t_1)构造函数]由题意,函数(f(x))有两个零点(x_1),(x_2)((x_1 eq x_2)),
即(f(x_1)=f(x_2)=0),易知(ln x_1),(ln x_2)是方程(x=acdot e^x)的两根.
设(t_1=ln x_1),(t_2=ln x_2),设(g(x)=xcdot e^{-x}),则(g(t_1)=g(t_2)),
从而(x_1x_2>e^2) (Leftrightarrow) (ln x_{_1}+ln x_2>2) (Leftrightarrow) (t_1+t_2>2).
以下证明:(t_1+t_2>2).
由(g(t_1)=g(t_2)),得(t_1e^{-t_1}=t_2e^{-t_2}),
化简得(e^{t_2-t_1}=cfrac{t_2}{t_1}),①
不妨设(t_2>t_1),由法一知,(0<t_1<1<t_2).
令(s=t_2-t_1),则(s>0),(t_2=s+t_1),
代入①式,得(e^s=cfrac{s+t_1}{t_1}),解得(t_1=cfrac{s}{e^s-1}).
则(t_1+t_2=2t_1+s=cfrac{2s}{e^s-1}+s),
故要证(t_1+t_2>2),即证(cfrac{2s}{e^s-1}+s>2),
即证(2s+(s-2)(e^s-1)>0),②
令(G(s)=2s+(s-2)(e^s-1)(s>0)),
则(G'(s)=(s-1)e^s+1),(G''(s)=se^s>0),
故(G'(s))在((0,+∞))上单调递增,所以(G'(s)>G'(0)=0),
从而(G(s))在((0,+∞))上单调递增,所以(G(s)>G(0)=0),
所以②式成立,故(t_1+t_2>2),故(x_1x_2>e^2).
[法2总结] 该方法的关键是巧妙引入变量(s),然后利用等量关系,把(t_1),(t_2)消掉,从而构造相应的函数,转化所证问题.其解题要点为:
(1). 取差构元:记(s=t_2-t_1),则(t_2=t_1+s),利用该式消掉(t_2),
(2). 巧解消参:利用(g(t_1)=g(t_2)),构造方程,解之,利用(s)表示(t_1),
(3). 构造函数:依据消参之后所得不等式的形式,构造关于(s)的函数(G(s)),
(4). 转化求解:利用导数研究函数(G(s))的单调性和最小值,从而证得结论.
【法三】:[巧抓“根商” — (c=cfrac{x_1}{x_2})构造函数]不妨设(x_1>x_2),
因为(ln x_1-ax_1=0),(ln x_2-ax_2=0),
所以(ln x_1+ln x_2=a(x_1+x_2)),(ln x_1-ln x_2=a(x_1-x_2)),所以(cfrac{ln x_1-ln x2}{x_1-x_2}=a),
欲证(x_1x_2>e^2),即证(ln x_1+ln x_2>2),
因为(ln x_1+ln x_2=a(x_1+x_2)),
所以即证(a>cfrac{2}{x_1+x_2}),
所以原问题等价于证明(cfrac{ln x_1-ln x_2}{x_1-x_2}>cfrac{2}{x_1+x_2}),
即(ln cfrac{x_1}{x_2}>cfrac{2(x_1-x_2)}{x_1+x_2}),
令(c=cfrac{x_1}{x_2}(c>1)),则不等式变为(ln c>cfrac{2(c-1)}{c+1}),
令(h(c)=ln c-cfrac{2(c-1)}{c+1}),(c>1),
所以(h'(c)=cfrac{1}{c}-cfrac{4}{(c+1)^2}=cfrac{(c-1)^2}{c(c+1)^2}>0),
所以(h(c))在((1,+∞))上单调递增,
所以(h(c)>h(1)=ln 1-0=0),即(ln c-cfrac{2(c-1)}{c+1}),(c>1),
因此原不等式(x_1x_2>e^2)得证.
[法3总结]:该方法的基本思路是直接消掉参数(a),再结合所证问题,巧妙引入变量(c=cfrac{x_1}{x_2}),从而构造相应的函数.其解题要点为:
(1). 联立消参:利用方程(f(x_1)=f(x_2))消掉解析式中的参数(a),
(2). 抓商构元:令(c=cfrac{x_1}{x_2}),消掉变量(x_1),(x_2),构造关于(c)的函数(h(c)),
(3). 用导求解:利用导数求解函数(h(c))的最小值,从而可证得结论.
(1).当(m=cfrac{1}{2})时,求函段(f(x))在区间([1,4])上的最值.
当(m=cfrac{1}{2})时,(f(x)=cfrac{1}{2} x+cfrac{1}{2}+cfrac{3}{2x}-ln x),函数(f(x))的定义域为((0,+infty))
所以(f^{prime}(x)=cfrac{1}{2}-cfrac{3}{2x^{2}}-cfrac{1}{x}=cfrac{(x+1)(x-3)}{2x^{2}}),
当(xin[1,3))时,(f^{prime}(x)<0),(f(x))单调递减,
当(xin(3,4])时,(f^{prime}(x)>0),函数(f(x))单调递增。
所以函数(f(x))在区间([1,4])上的最小值为(f(3)=cfrac{5}{2}-ln3),
又(f(1)=cfrac{1}{2}+cfrac{1}{2}+cfrac{3}{2}-ln1=cfrac{5}{2}),
(f(4)=cfrac{23}{8}-2ln2),显然(f(1)>f(4)),
所以函数(f(x))在区间([1,4])上的最小值为(cfrac{5}{2}-ln3),最大值为(cfrac{5}{2})。
(2).若(x_{1}),(x_{2})是函数(g(x)=xf(x))的两个极值点,且(x_{1}<x_{2}),求证:(x_{1}x_{2}<1).
证明: 因为(g(x)=xf(x)=cfrac{1}{2}x^{2}+mx+cfrac{3}{2}-xln x),
所以(g^{prime}(x)=x+m-(1+ln x)),因为函数(g(x))有两个不同的极值点,
所以(g^{prime}(x)=x+m-(1+ln x)),有两个不同的零点,
因此(m=1-x+ln x)有两个不同的实数根,
令(p(x)=1-x+ln x),则(p^{prime}(x)=cfrac{1-x}{x}),
当(xin(0,1))时,则(p^{prime}(x)>0),函数(p(x))单调递增;
当(xin(1,+infty)),则(p^{prime}(x)<0),函数(p(x))单调递减增;
所以函数(p(x))的最大值为(p(1)=1-1+ln 1=0)
所以当直线(y=m)与函数图像有两个不同的交点时,有(m<0)且(0<x_{1}<1<x_{2})
要证(x_{1}x_{2}<1),只要证(x_{2}<cfrac{1}{x_{1}}),
易知函数(q(x)=g^{prime}(x)=x+m-(1+ln x))在((1,+infty))上单调递增
所以只需证(q(x_{2})<q(cfrac{1}{x_{1}})),又由题可知(q(x_{2})=q(x_{1})=0)
所以(m=1-x_{1}+ln x_{1}),
即证 (q(cfrac{1}{x_{1}})=cfrac{1}{x_{1}}+m-1-ln cfrac{1}{x_{1}}=cfrac{1}{x_{1}}+1-x_{1}+ln x_{1}-1-ln cfrac{1}{x_{1}}=cfrac{1}{x_{1}}-x_{1}+2 ln x_{1}>0)
记(h(x)=cfrac{1}{x}-x+2ln x),则(h^{prime}(x)=-cfrac{1}{x^{2}}-1+cfrac{2}{x}=-cfrac{(x-1)^{2}}{x^{2}}<0) 恒成立
所以函数(h(x))在(xin(0,1))上单调递减,所以当(xin(0,1))时,(h(x)>h(1)=1-1=0)
所以(q(cfrac{1}{x_{1}})>0),因此 (x_{1} x_{2}<1)。
(1).试确定函数(f(x))的零点个数;
分析:碰到这样的函数的零点个数问题,我们一般不应该想到通过解方程[从数的角度]来求解得到,原因是函数是个超越函数,其中含有(e^x)的因子,而应该想到通过形的角度思考,转化为两个函数的图像的交点个数问题。
解析:由 (f(x)=0) 得 (a=(2-x)cdot e^x),令 (g(x)=(2-x)cdot e^x),
则函数(f(x)) 的零点个数即直线 (y=a) 与曲线 (g(x)=(2-x)cdot e^x) 的交点个数;
以下的难点和重点是如何作出函数(g(x))的图像;由于函数的形式复杂,故想到用导数工具;
函数(g(x))的定义域为((-infty,+infty)),由于(g'(x)=-1cdot e^x+(2-x)cdot e^x=(1-x)cdot e^x),
由 (g'(x)>0) 得 (x<1), 故函数 (g(x)) 在 ((-infty,1))上单调递增,
由 (g'(x)<0) 得 (x>1), 故函数 (g(x)) 在 ((1,+infty))上单调递减,
由于(x=1) 时,函数 (g(x)) 有最大值, (g(x)_{max }=g(1)=e);
又当 (x<2) 时,(g(x)>0),(g(2)=0),当 (x>2) 时, (g(x)<0),
作出函数 (g(x)) 的大致图像如图所示,
由图像可知,
当(aleqslant 0)时,函数(y=a)与函数(g(x))的交点个数为一个,故函数(f(x))的零点个数为一个;
当(0<a<e)时,函数(y=a)与函数(g(x))的交点个数为两个,故函数(f(x))的零点个数为两个;
当(a=e)时,函数(y=a)与函数(g(x))的交点个数为一个,故函数(f(x))的零点个数为一个;
当(a>e)时,函数(y=a)与函数(g(x))的交点个数为零个,故函数(f(x))的零点个数为零个;
(2).设(x_1),(x_2)是函数(f(x))的两个零点,证明:(x_1+x_2<2);
法一:函数 (f(x)) 的零点即直线 (y=a) 与曲线 (g(x)=(2-x)e^{x}) 的交点的横坐标,
由(1)知 (0<a<e),不妨设 (x_{1}<1<x_{2}),得 (2-x_{2}<1),
由函数 (g(x)=(2-x)e^{x}) 在 ((-infty,1))上单调递增,在((1,+infty))上单调递减,
函数 (f(x)=-g(x)+a) 在 ((-infty, 1))上单调递减,在((1,+infty))上单调递增;
要证 (x_{1}+x_{2}<2),只需证 (x_{1}<2-x_{2}),只需证 (f(x_{1})>f(2-x_{2})),
又 (f(x_{1})=0),故要证 (f(2-x_{2})<0),
由 (a=g(x_{2})) 得 (f(2-x_{2})=-x_{2}e^{2-x_2}+a=-x_{2}e^{2-x_2}-(x_2-2)e^{x_2}(x_{2}>1))
构造函数 (h(x)=-xe^{2-x}-(x-2)e^{x}),则 (h'(x)=(1-x)(e^{x}-e^{2-x})),
当 (x>1) 时, (e^{x}>e^{2-x}),(h'(x)<0),故函数 (h(x)) 在 ((1,+infty)) 上单调递减,
当 (x>1) 时,(h(x)<h(1)=0),
即当 (x_{2}>1) 时, (f(2-x_{2})<0), 即 (x_{1}+x_{2}<2);
法二: 由(1)知 (0<a<e),不妨设 (x_{1}<1<x_{2}),设 (F(x)=f(x)-f(2-x)(x>1)),
则 (F(x)=(x-2)e^{x}+xe^{2-x}),(F'(x)=(1-x)(e^{2-x}-e^{x}))
易知 (y=e^{2-x}-e^{x}) 是减函数, 故当 (x>1) 时,(e^{2-x}-e^{x}<e-e=0),
又 (1-x<0), 故 (F'(x)>0), (F(x)) 在 ((1,+infty)) 上单调递增,
故当 (x>1) 时,(F(x)>0),即 (f(x)>f(2-x)),
由 (x_{2}>1) 得 (f(x_{2})>f(2-x_{2})),又 (f(x_{2})=0=f(x_{1})),
故(f(2-x_{2})<f(x_{1}))
由 (g(x)=(2-x)e^{x}) 在 ((-infty,1))上单调递增,得 (f(x)=-g(x)+a) 在 ((-infty,1))上单调递减,
又 (2-x_{2}<1), (2-x_{2}>x_{1}),即(x_{1}+x_{2}<2);