前言
涉及公式
| 面积 | 体积 | |
|---|---|---|
| 圆柱 | $S_{侧}=2pi rh$ | $V=Sh=pi r^2h$ |
| 圆锥 | $S_{侧}=pi r l$ | $V=cfrac{1}{3}Sh=cfrac{1}{3}pi r^2 h=cfrac{1}{3}pi r^2 sqrt{l^2-r^2}$ |
| 圆台 | $S_{侧}=pi(r_1+r_2)l$ | $V=cfrac{1}{3}(S_{上}+S_{下}+sqrt{S_{上}S_{下}})h=cfrac{1}{3}pi(r_1^2+r_2^2+r_1r_2)h$ |
| 直棱柱 | $S_{侧}=Ch$ | $V=Sh$ |
| 棱锥 | $S_{侧}=cfrac{1}{2}Ch'$ | $V=cfrac{1}{3}Sh$ |
| 棱台 | $S_{侧}=cfrac{1}{2}(C+C')h'$ | $V=cfrac{1}{3}(S_{上}+S_{下}+sqrt{S_{上}S_{下}})h$ |
| 球体 | $S_{侧}=4pi R^2$ | $V=cfrac{4}{3}pi R^3$ |
技巧总结
常运用割补法,
典例剖析
分析:如图所示,(OA=R),(MD=r),则(AM=cfrac{3R}{2}),(BM=cfrac{R}{2}),
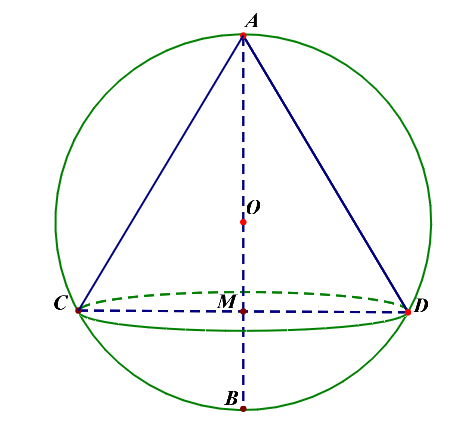
由相交弦定理(垂径定理)可知,(r^2=cfrac{3R}{2}cdot cfrac{R}{2}=cfrac{3R^2}{4}),圆锥的高(h=AM=cfrac{3R}{2})
则(V_{圆锥}=cfrac{1}{3}pi r^2 h=cfrac{3pi R^3}{8}=cfrac{3pi}{8}),故(R=1),故(S_{球}=4pi R^2=4pi).
已知三棱锥(P-ABC)满足(PA、PB、PC)两两垂直,且(PA=PB=PC=2),(Q)是三棱锥(P-ABC)外接球上的一个动点,则点(Q)到平面(ABC)的距离的最大值是多少?
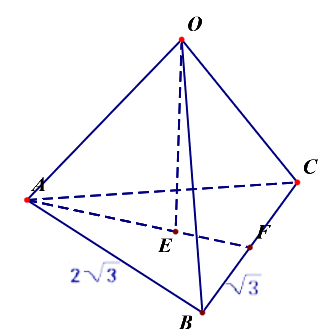
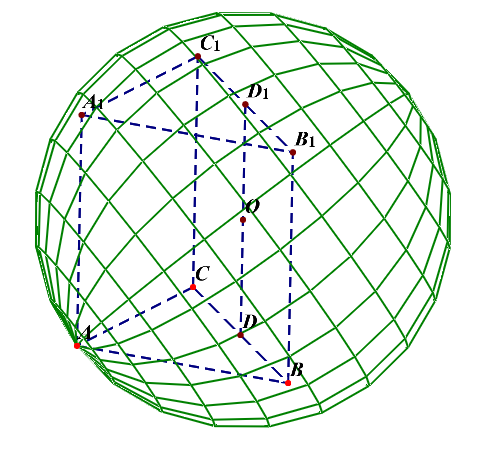
分析:我们可以将此三棱锥还原为正方体的一部分,补体并特殊化为为正方体的一个角,如图所示,

且正方体有个外接球,那么点(Q)到平面(ABC)的距离的最大值即是正方体的体对角线的(cfrac{2}{3}),而体对角线长为(sqrt{2^2+2^2+2^2}=2sqrt{3}),故所求值为(cfrac{4sqrt{3}}{3})。
分析:本题目关键是求球的半径(R) ,如上例中的模型,已知的三点可以安放在图中的点(A'、B、C')处,但是要注意,
已知的平面(ABC)和模型中的平面(A'BC')平行,不一定重合,此时求半径问题就转化为求正三棱锥的侧棱的长问题了,
而且此时正三棱锥的底面边长为(2sqrt{3}),正三棱锥的高是1,高的垂足(E)是下底面的中心,
则其侧棱(OA),(OA=sqrt{1^2+2^2}=sqrt{5}),故(R=sqrt{5}),
故该球的体积(V_球=cfrac{4}{3}cdot picdot R^3=cfrac{20sqrt{5}}{3}pi)。
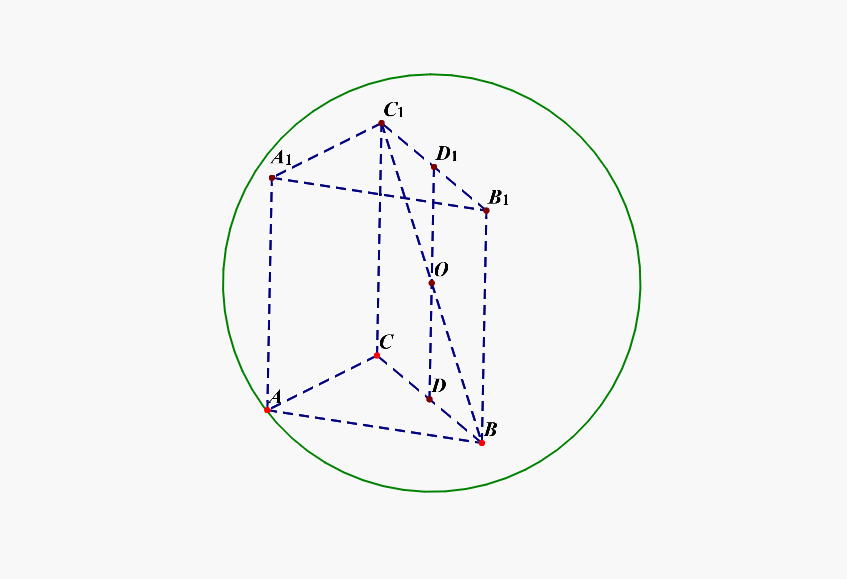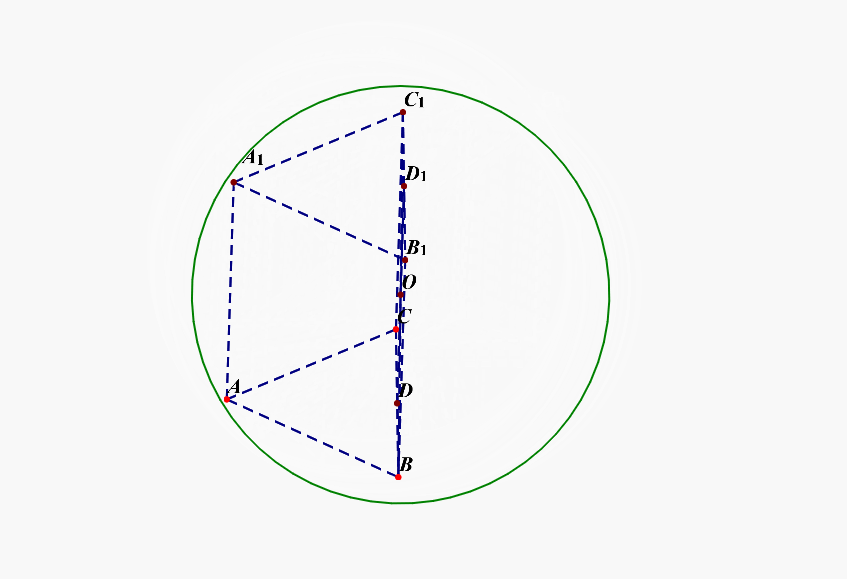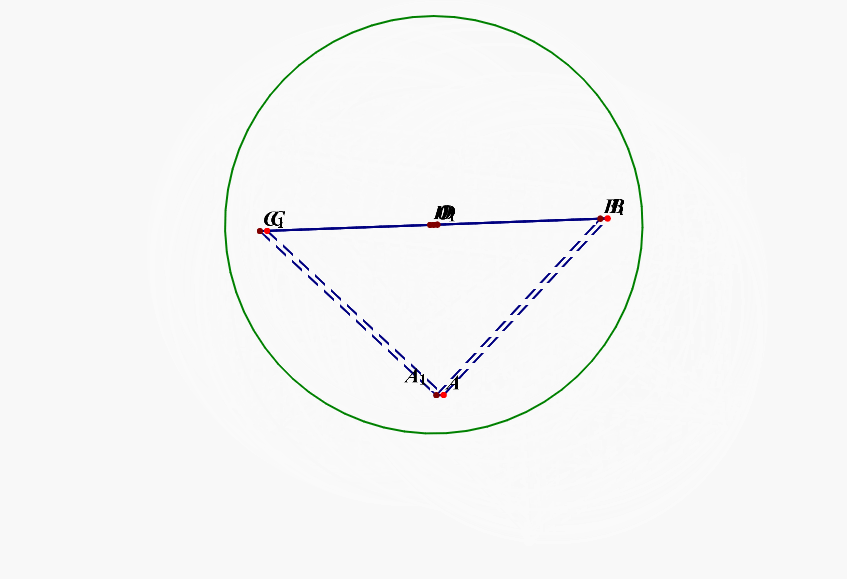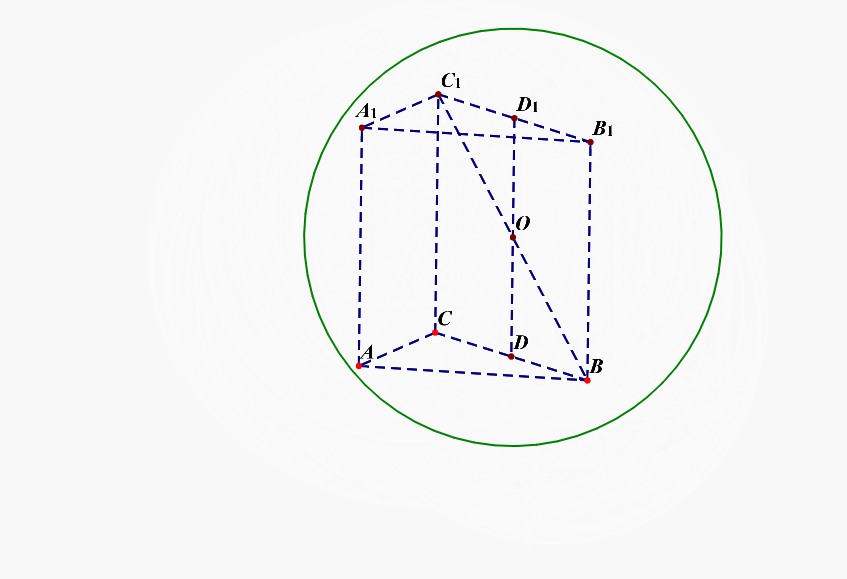
分析:平面图形如左图,立体图形如右图所示,(angle MAC=angle MAD=cfrac{pi}{2}),下来的重点是如何将四面体放置在球体内部。
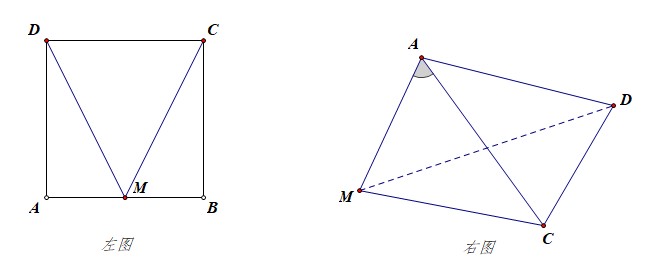
可以这样来思考,将最特殊的面(ACD)放置在下底面,这样方便来放置和下底面垂直的侧棱,如下图所示;
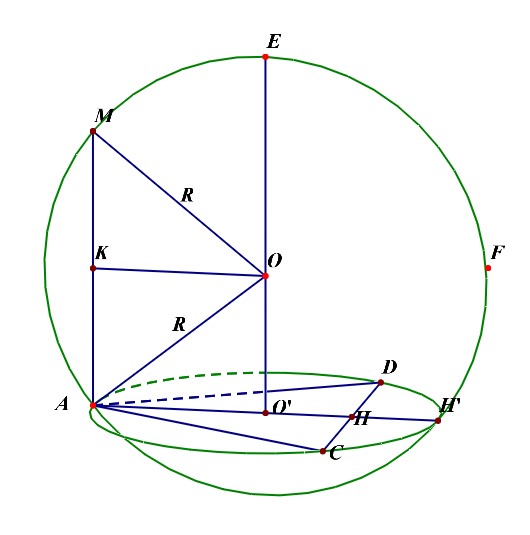
底面圆的圆心(O')为下底面正三角形的重心,(O)为球心,则(OA=OM=R),由于( riangle ACD)为等边三角形,(AC=2),则(CH=1),(AH=sqrt{3}),则(AO'=cfrac{2sqrt{3}}{3}),过点(O)做(OKperp AM)于(K),则(OK=AO'=cfrac{2sqrt{3}}{3}),又(AK=cfrac{1}{2}AM=cfrac{1}{2}),在(Rt riangle AOK)中,由勾股定理可知(R^2=(cfrac{2sqrt{3}}{3})^2+(cfrac{1}{2})^2=cfrac{19}{12}),故(S_{球O}=4pi R^2=cfrac{19pi}{3})。
补充说明:如果想不清这一点,还可以想着将四面体补体成一个直三棱柱,如下图的动图所示,
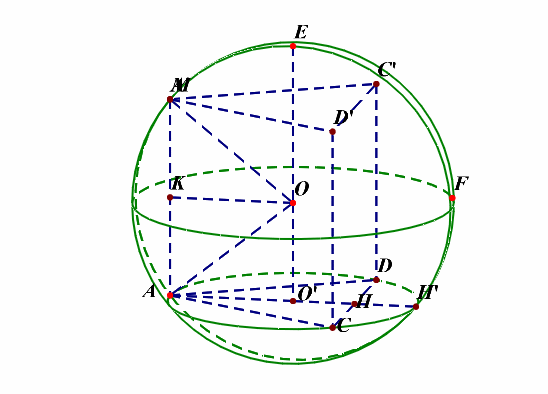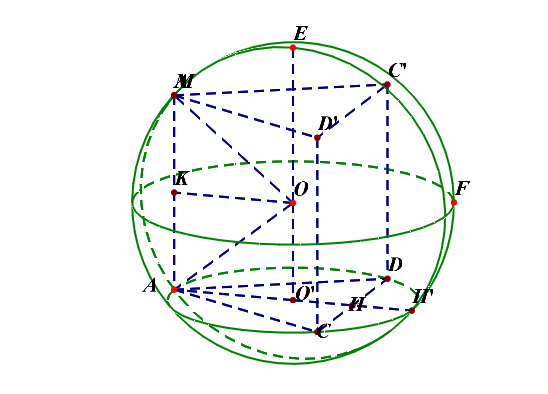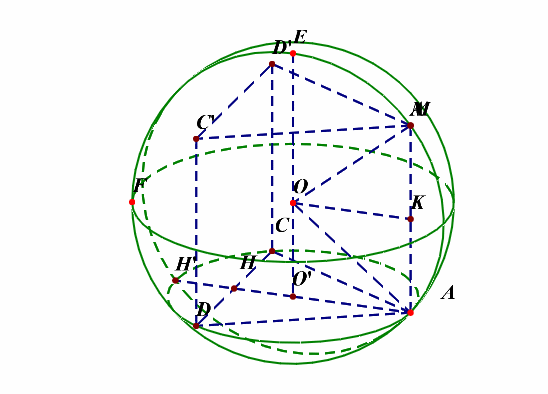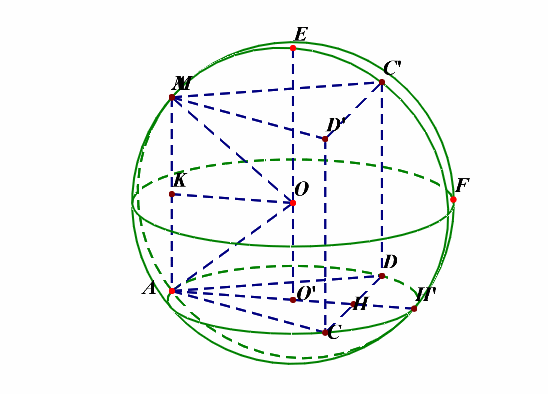
解后反思:当一条侧棱和下底面垂直时,常将三棱锥(M-ACD)补体成直三棱柱(MC'D'-ACD),这样容易想清楚。
分析:有空整理;
分析:补体并特殊化为为正方体的一个角,如图所示,

则体对角线长为(3sqrt{3}),即(R=cfrac{3sqrt{3}}{2}),故(S_{表}=4pi R^2=27pi).
分析:如图,设( riangle ABC)的外接圆的圆心为(E),由于三棱锥(P-ABC)的所有棱长都相等,故三棱锥为正四面体,

设正四面体的棱长为(AB=a),由正四面体的体积为(V=cfrac{9sqrt{2}}{4}),可解得(a=3),
则其外接球的半径为(R=cfrac{sqrt{6}a}{4}=cfrac{3sqrt{6}}{4}),详解详析 [1]
故三棱锥(P-ABC)的外接球的表面积为(S=4pi R^2=4pi (cfrac{sqrt{6}3}{4})^2=cfrac{27pi}{2}),故选(A)。
分析:由于鲁班锁的上下、左右、前后完全对称,故此问题等同于一个下底面的长为(2)宽为(4),高为(5)的长方体外接于球,如图所示,

则外接球的直径为长方体的体对角线,则其长为(sqrt{2^2+4^2+5^2}=3sqrt{5}),则(R=cfrac{3sqrt{5}}{2}),
故球体的表面积为(4pi R^2=45pi),故选(C).
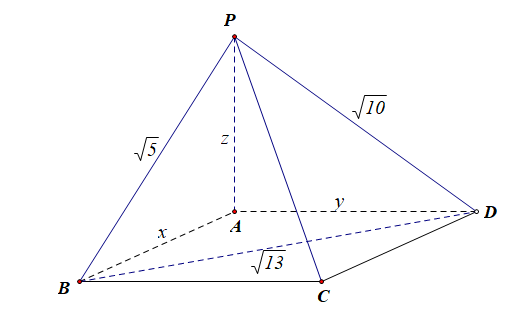
分析:如图所示,(PA),(AB),(AD)两两垂直,设(AB=x),(AD=y),(AP=z),则有
(x^2+y^2=13),(y^2+z^2=10),(z^2+x^2=5),则可知(x^2+y^2+z^2=14),
故将此三棱锥还原为长方体后,其体对角线(d=sqrt{14}),则(P-ABCD)的外接球的半径为(r=cfrac{sqrt{14}}{2}),
故(S_{球}=4pi r^2=4pi cdot cfrac{14}{4}=14pi),故选(D).
分析:设此三棱柱的底面直角三角形的直角边分别为(a),(b),则棱柱的高(h=sqrt{a^2+b^2}),
设直三棱柱的外接球的半径为(R),则(cfrac{4}{3}pi R^3=cfrac{32pi}{3}),解得(R=2),
由于上下底面三角形的斜边的中点的连线的中点为该三棱柱的外接球的球心,
故(sqrt{2}h=2R=4),则(h=2sqrt{2}),所以(a^2+b^2=h^2=8geqslant 2ab),
则(ableqslant 4),当且仅当(a=b=2)时取到等号。
故三棱柱的体积(V=Sh=cfrac{1}{2}abh=sqrt{2}ableq 4sqrt{2})。