有价值的题目:4,8,9,10,11,12,13,14,15,16
分析:由于((a+b)^n)的二项展开式的通项公式为(T_{r+1}=C_n^rcdot a^{n-r}cdot b^r),
故(T_{r+1}=C_n^rcdot x^{n-r}cdot (-cfrac{1}{sqrt{x}})^r=(-1)^rcdot C_n^rcdot x^{n-cfrac{3r}{2}}),
则(n-cfrac{3r}{2}=0),且(m=r+1),代入整理得到,(2n=3(m-1)),故选(A)。
分析:将题目中的圆锥展开后,则其侧面形成一个半径为(13),弧长为(10pi)的扇形,如下图所示,
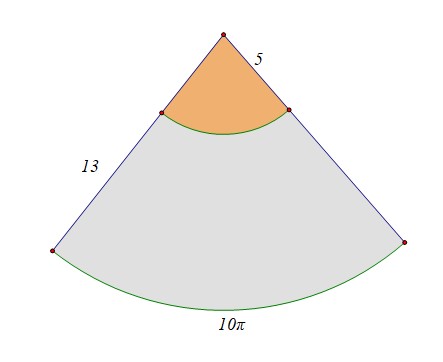
要使的蚂蚁距离圆锥顶点超过5cm,则蚂蚁应该在扇环内部,而小扇形的弧长可以这样计算(cfrac{l}{5}=cfrac{10pi}{13}),故小扇形的弧长为(cfrac{50pi}{13}),
故所求概率为(P=1-cfrac{cfrac{1}{2} imes cfrac{50pi}{13} imes 5}{cfrac{1}{2} imes 10pi imes 13}=cfrac{144}{169}),故选(C)。
分析:简单记录思路,由(a_n)与(S_n)的关系先求得(a_n=cfrac{2n-13}{t}),利用(a_2+a_4=28),求得(t=-cfrac{1}{2}),
这样(a_n=26-4n),令(a_n>0),解得(nleq 6),由邻项变号法可知,(S_6)最大,故选(B)。
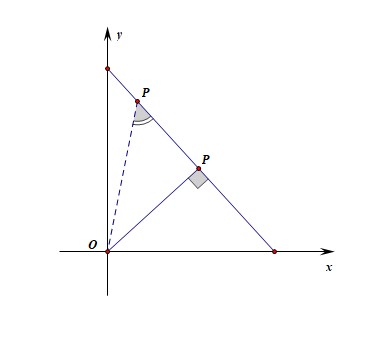
法1:从形的角度思考,采用坐标法求解;以点(A)为坐标原点建立如图所示的直角坐标系,
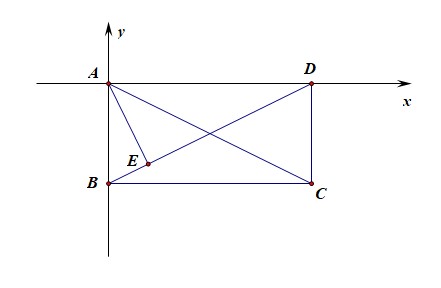
则可知(A(0,0)),(B(0,-2)),(C(4,-2)),(D(4,0)),设(E(x,y)),
则由(k_{AE}cdot k_{BD}=-1),可得(y=-2x)①,又直线(BD:2y=x-4)②,
联立①②可得,(x=cfrac{4}{5}),(y=-cfrac{8}{5}),
则(overrightarrow{AE}cdot overrightarrow{AC}=(cfrac{4}{5},-cfrac{8}{5})cdot (4,-2)=cfrac{32}{5}),故选(C).
法2:本题目是否还可以用基向量法,以(overrightarrow{AB})和(overrightarrow{AD})为基向量来表示其他向量,待思考;
分析:如图所示,直线过抛物线的焦点,故利用抛物线的焦点弦长公式可得,(cfrac{2p}{sin^2 heta}=17),
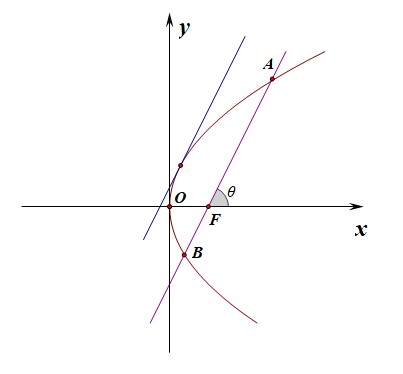
又由于直线的斜率(k=4),则(sin^2 heta=cfrac{2p}{17}),(cos^2 heta=cfrac{17-2p}{17}),则(k^2=16=tan^2 heta=cfrac{2p}{17-2p}),
解得(p=8),从而(a=16),抛物线为(y^2=16);
由图可知所求直线和抛物线相切于第一象限,故涉及到的函数为(y=f(x)=4sqrt{x}),
设切点为(P(x_0,y_0)),则(f'(x_0)=cfrac{2}{sqrt{x_0}}=4),求得(x_0=cfrac{1}{4}),(y_0=2),
又所求直线的(k=4),由点斜式方程可得,所求直线为(4x-y+1=0),故选(B).
解后反思:焦点弦的公式不止一个,此处选用这一个就是考虑变量少,运算简单。
法1:先考虑分离参数法,若能成功分离参数,那么得到的形式必然是(m>g(x))或(m<g(x))的形式,接下来需要求解函数(g(x))的最值,其必然是数字化的,则结果和给定的选项的形式是不一致的,故这个思路做了大致分析后放弃;
法2:由函数(f(x)>0)恒成立,则需要求在((0,+infty))上的函数(f(x)_{min}>0)即可,故考虑用导数方法;
(f'(x)=cfrac{(x+1)[mx+(1-m)]}{x^2}), 故函数在(x=cfrac{m-1}{m})处取到最小值,则要使得函数(f(x)>0)恒成立,只需要(f(cfrac{m-1}{m})>0)即可,
对此化简整理得到,正实数(m)应该满足(cfrac{m-1}{m}cdot e^{2m-1}>1),故选(C)。
解后反思:本题目的解法有点漏洞,条件中应该使得(m>1),而不仅仅是(m>0),否则当(0<mleq 1)时,函数(f(x))在((0,+infty))上单调递增,其最小值的极限为(f(0)),题目就有了问题。
分析:做出如图所示的三角形可行域,三条边长可知,故求其外接圆的半径可以采用(S_{ riangle OAB}=cfrac{abc}{4R}),
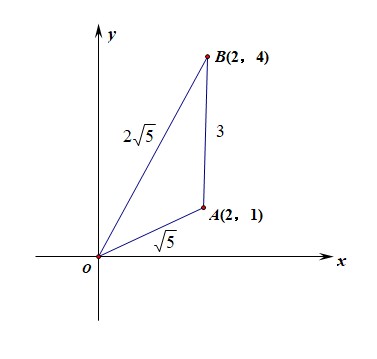
又由于(S_{ riangle OAB}=cfrac{1}{2} imes 3 imes 2=3),则(3=cfrac{3 imes sqrt{5} imes 2sqrt{5}}{4R}),解得(R=cfrac{5}{2}),故(S_{外接圆}=cfrac{25pi}{4})。
解后反思:结合题目的具体条件,选择恰当的公式,计算量能相应的减少。
法1:由已知条件可知,(m+n=16),若从数的角度入手分析,则(m=16-n),
转化为先求(m^2+n^2=(16-n)^2+n^2=2n^2-32n+16^2=2(n-8)^2+128),
故((m^2+n^2)_{min}=128),故所求最小值为(sqrt{128}=8sqrt{2})。
法2:由已知条件可知,(m+n=16),若从形的角度入手分析,建立如图所示的坐标系,
可知,(m+n=16)表示一条直线,(sqrt{m^2+n^2}=sqrt{(m-0)^2+(n-0)^2})表示定点((0,0))与动点((m,n))的距离,
故所求的最小距离为(8sqrt{2})。
分析:如下图所示,可知圆(F_2)的圆心为(F_2(c,0)),半径为(r=cfrac{c}{2}),由于圆和双曲线都关于坐标轴对称,故只需要保证圆和一条渐近线(y=cfrac{b}{a}x)有公共点即可,
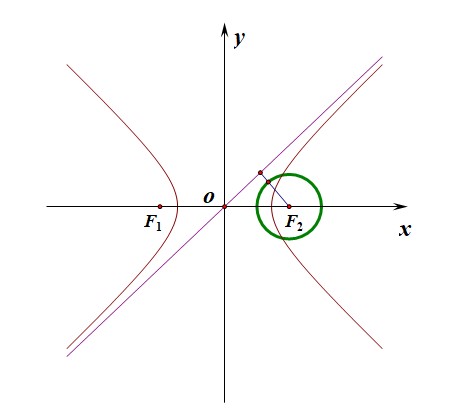
此时可以使用联立直线方程和双曲线的方程,使用(Delta ge 0)的思路,也可以利用圆心到直线的距离小于半径的思路,很明显第二个思路的运算量要小一些。
此时圆心为(F_2(c,0)),半径为(r=cfrac{c}{2}),直线为(bx-ay=0),故(d=cfrac{|bc-a imes 0|}{sqrt{a^2+b^2}}leq cfrac{c}{2}),
化简整理得到,(2bleq c),即(4b^2leq c^2),则(4c^2-4a^2leq c^2),整理为(cfrac{c^2}{a^2}leq cfrac{4}{3}),故(eleq cfrac{2sqrt{3}}{3}),又双曲线的(e>1),故(ein (1,cfrac{2sqrt{3}}{3}]).
分析:平面图形如左图,立体图形如右图所示,(angle MAC=angle MAD=cfrac{pi}{2}),下来的重点是如何将四面体放置在球体内部。
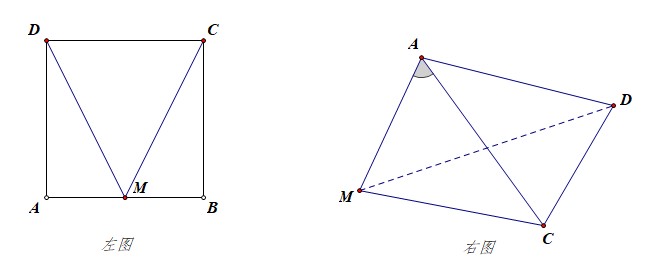
可以这样来思考,将最特殊的面(ACD)放置在下底面,这样方便来放置和下底面垂直的侧棱,如下图所示;
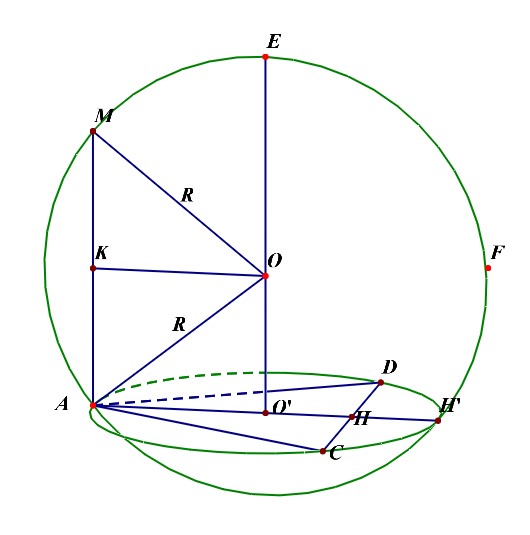
底面圆的圆心(O')为下底面正三角形的重心,(O)为球心,则(OA=OM=R),由于( riangle ACD)为等边三角形,(AC=2),则(CH=1),(AH=sqrt{3}),则(AO'=cfrac{2sqrt{3}}{3}),过点(O)做(OKperp AM)于(K),则(OK=AO'=cfrac{2sqrt{3}}{3}),又(AK=cfrac{1}{2}AM=cfrac{1}{2}),在(Rt riangle AOK)中,由勾股定理可知(R^2=(cfrac{2sqrt{3}}{3})^2+(cfrac{1}{2})^2=cfrac{19}{12}),故(S_{球O}=4pi R^2=cfrac{19pi}{3})。
补充说明:如果想不清这一点,还可以想着将四面体补体成一个直三棱柱,如下图的动图所示,
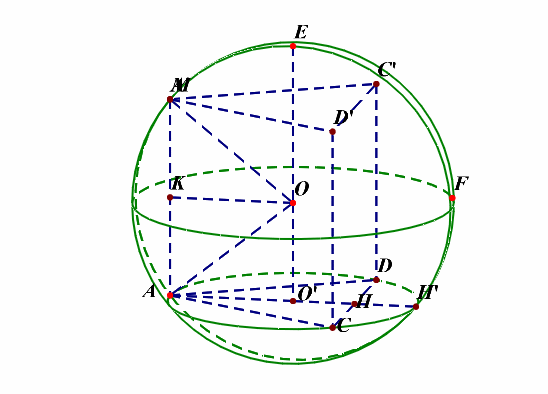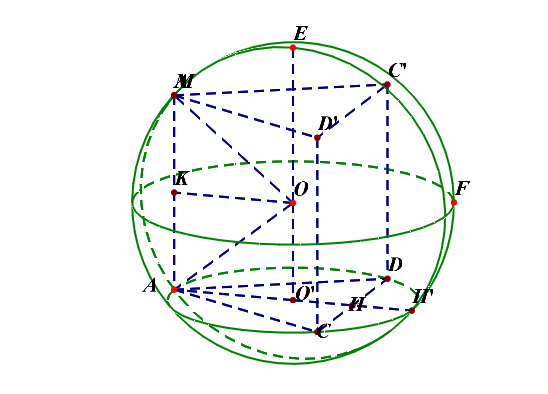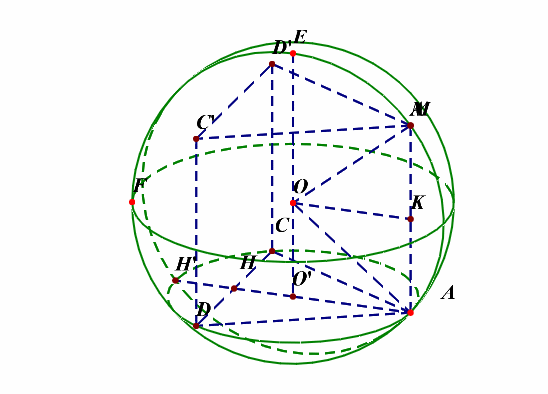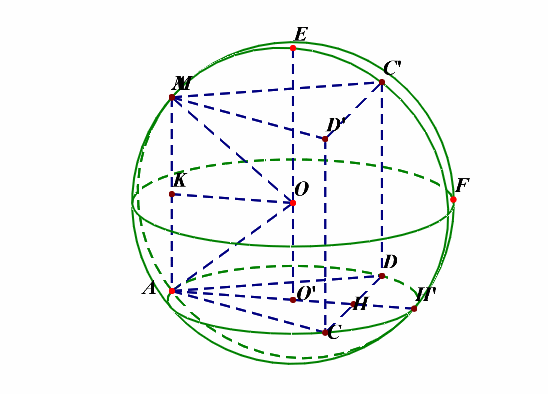
解后反思:当一条侧棱和下底面垂直时,常将三棱锥(M-ACD)补体成直三棱柱(MC'D'-ACD),这样容易想清楚。