归纳推理
-
涉及表达式类的归纳推理,
-
涉及数列类的归纳推理,常常考查二阶等差数列(({a_{n+1}-a_n})为等差数列)和斐波那契数列,
类比推理
-
元素之间的类比结论:点(Rightarrow)线,线(Rightarrow)面,面(Rightarrow)体,
-
几何体之间的类比结论:三角形(Rightarrow)四面体,正三角形(Rightarrow)正四面体,(Rt riangle)三角形(Rightarrow)直三面角的四面体(墙角),内切圆(Rightarrow)内切球,
-
几何体位置关系之间的类比结论:平面内平行(Rightarrow)空间内平行,平面内垂直(Rightarrow)空间内垂直,
-
运算符号之间的类比结论:差(Rightarrow)比,和(Rightarrow)积,积(Rightarrow)乘方,商(Rightarrow)开方,取对数(Rightarrow)取指数,
-
测度之间的类比结论:长度(Rightarrow)面积,面积(Rightarrow)体积,圆的半径(Rightarrow)椭圆的焦半径,,内切圆(外接圆)面积(Rightarrow)内切球(外接球)体积,
-
运算法则之间的类比结论:有理数运算法则(Rightarrow)实数运算法则,实数运算法则(Rightarrow)复数运算法则,
-
证明方法之间的类比结论:等面积法(Rightarrow)等体积法,
-
对应数字之间的类比结论:(2Rightarrow 3),(sqrt[2]{??}Rightarrow sqrt[3]{??}),(3Rightarrow 4),(cfrac{1}{3}Rightarrow cfrac{1}{4}),
-
涉及数列类的类比推理,由等差数列的性质类比到等比数列的性质。
演绎推理
- 演绎推理的主要形式:三段论。
分析:上述的推理形式就是演绎推理,但是结果却是错误的。原因是大前提不正确。
典例剖析
(cfrac{3}{1 imes 2} imes cfrac{1}{2}=1-cfrac{1}{2^2}),
(cfrac{3}{1 imes 2} imes cfrac{1}{2}+cfrac{4}{2 imes 3} imes cfrac{1}{2^2}=1-cfrac{1}{3 imes 2^2}),
(cfrac{3}{1 imes 2} imes cfrac{1}{2}+cfrac{4}{2 imes 3} imes cfrac{1}{2^2}+cfrac{5}{3 imes 4} imes cfrac{1}{2^3}=1-cfrac{1}{4 imes 2^3}),
(cdots),(cdots),
由以上等式推测到一个一般性的结论为:?
(cfrac{3}{1 imes 2} imes cfrac{1}{2}+cfrac{4}{2 imes 3} imes cfrac{1}{2^2}+cfrac{5}{3 imes 4} imes cfrac{1}{2^3}+cdots+cfrac{n+2}{n imes(n+1)} imes cfrac{1}{2^n}=1-cfrac{1}{(n+1) imes 2^n})。
(1+cfrac{1}{2^2}<cfrac{3}{2});
(1+cfrac{1}{2^2}+cfrac{1}{3^2}<cfrac{5}{3});
(1+cfrac{1}{2^2}+cfrac{1}{3^2}+cfrac{1}{4^2}<cfrac{7}{4});
(cdots),(cdots),
由以上等式推测到一个一般性的结论为:?
(1+cfrac{1}{2^2}+cfrac{1}{3^2}+cfrac{1}{4^2}+cdots+cfrac{1}{n^2}<cfrac{2n-1}{n}(nge 2,nin N^*));
在凸四边形(ABCD)中,不等式(cfrac{1}{A}+cfrac{1}{B}+cfrac{1}{C}+cfrac{1}{D}ge cfrac{16}{2pi})成立;
在凸五边形(ABCDE)中,不等式(cfrac{1}{A}+cfrac{1}{B}+cfrac{1}{C}+cfrac{1}{D}+cfrac{1}{E}ge cfrac{25}{3pi})成立;
(cdots),(cdots),以此类推,?
在凸(n)边形(A_1A_2A_3cdots A_n)中,不等式(cfrac{1}{A_1}+cfrac{1}{A_2}+cfrac{1}{A_3}+cdots+cfrac{1}{A_n}ge cfrac{n^2}{(n-2)pi}(nge 3,nin N^*))成立;
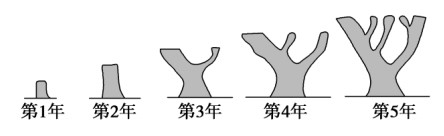
分析:本题目涉及到的数列为“斐波那契数列”,其构成规律为:(a_1),(a_2)已知,其他项由递推公式(a_{n+2}=a_{n+1}+a_n,nin N^*)得到,
故(a_6=8),(a_7=13),(a_8=21),(a_9=34),(a_{10}=55),(a_{11}=89),故选(D)。
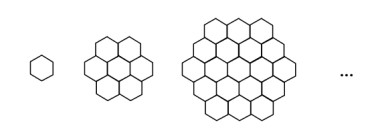
法1:注意到蜂巢个数所成的数列是二阶等差数列,我们可以这样做:
(1stackrel{+6}{longrightarrow}7); (7stackrel{+2 imes 6}{longrightarrow}19);(19stackrel{+3 imes 6}{longrightarrow}37);(37stackrel{+4 imes6}{longrightarrow}61);(61stackrel{+5 imes6}{longrightarrow}91);(91stackrel{+6 imes6}{longrightarrow}127);故选(C)。
法2:利用二阶等差数列和累加法求解;令蜂巢个数为(f(n)),则(f(1)=1),(f(2)=7),(f(3)=19),(f(4)=37),由于
(f(2)-f(1)=7-1=1 imes 6);
(f(3)-f(2)=19-7=2 imes 6);
(f(4)-f(3)=37-19=3 imes 6);
(f(5)-f(4)=61-37=4 imes 6);
$cdots $,
(f(n)-f(n-1)=6 imes (n-1));
因此,当(nge 2)时,由累加法可知,
(f(n)-f(1)=6 imes [1+2+3+cdots+(n-1)]=3n(n-1));
故(f(n)=3n^2-3n+1);
当(n=1)时,(f(1)=1=3 imes1^2-3 imes1+1),符合上式,
故蜂巢个数为(f(n)=3n^2-3n+1),
故可以计算(f(6)=91),当然也可以得到(f(10)=271);
求(f(1)),(f(2)),(f(3)),(f(4)),(f(5))的值;并总结(f(n))的表达式。
解析:由题意知,则(f(1)=2),(f(2)=4),(f(3)=7),(f(4)=11),(f(5)=16),
(f(2)-f(1)=4-2=2);
(f(3)-f(2)=7-4=3);
(f(4)-f(3)=11-7=4);
(f(5)-f(4)=16-11=5);
$cdots $,
(f(n)-f(n-1)=n);
因此,当(nge 2)时,由累加法可知,
(f(n)-f(1)=2+3+cdots+n=cfrac{(n+2)(n-1)}{2})
即(f(n)=cfrac{n^2+n+2}{2})
当(n=1)时,(f(1)=2),也满足上式,故
(f(n)=cfrac{n^2+n+2}{2})。
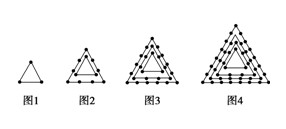
(1)求出(f(2)),(f(3)),(f(4)),(f(5));
分析:由题意可知,
(f(1)=3),
(f(2)=f(1)+3+3 imes 2=12),
(f(3)=f(2)+3+3 imes 4=27),
(f(4)=f(3)+3+3 imes 6=48),
(f(5)=f(4)+3+3 imes 8=75),
(2)找出(f(n))与(f(n+1))的关系,并求出(f(n))的表达式.
分析:由题意及(1)可知,
(f(n+1)=f(n)+3+3 imes 2n=f(n)+6n+3),
即(f(n+1)-f(n)=6n+3),
则(f(2)-f(1)=6 imes 1+3),
(f(3)-f(2)=6 imes 2+3),
(f(4)-f(3)=6 imes 3+3),
(cdots),(cdots),
(f(n)-f(n-1)=6 imes (n-1)+3),
利用累加法可知,当(nge 2)时,
(f(n)-f(1)=6[1+2+cdots+(n-1)]+3(n-1)=6 imes cfrac{n(n-1)}{2}+3(n-1)=3n^2-3),
即(f(n)=3n^2),当(n=1)时,满足上式,
故(f(n)=3n^2(nin N^*))。
分析:平面内的直角三角形中,两条直角边的平方之和等于斜边的平方,
空间内的直三面角中,三个侧面的面积平方之和为斜底面的面积的平方,
即(S_1^2+S_2^2+S_3^2=S^2),
平面内正三角形的内切圆的圆心、外接圆的圆心,是正三角形的内心;在正三角形的高线的靠近底边的三等分点处;
空间内正四面体的内切球的球心、外接球的球心,是正四面体的(类内心);在正四面体的高线的靠近底面的四等分点处;
注意:等面积法,等体积法;
分析:由题目可知,数列({a_n})是等和数列,也是周期数列,由(a_n+a_{n+1}=cfrac{1}{2})得到数列的前(21)项如下:
(-cfrac{3}{2},2,-cfrac{3}{2},2,-cfrac{3}{2},2,cdots,-cfrac{3}{2}),
则(S_{21}=10 imes (-cfrac{3}{2}+2)-cfrac{3}{2}=cfrac{7}{2})。
小结:等和数列大多表现为摆动数列或常数列。
分析:由等积数列的定义和已知条件,可以计算得到数列的各项如下,数列为周期数列,周期为(3),一个周期内的三项分别为(1,2,4);
(-1,2,4,-1,2,4,-1,2,4,cdots,-1,2,4,),
故(S_{12}=(1+2+4) imes 4=28)。
- (1)圆内接正方形的中心就是圆心,正方形的对角线的长度就是圆的直径;球内接正方体的中心就是球心,正方体的体对角线的长度就是球的直径。
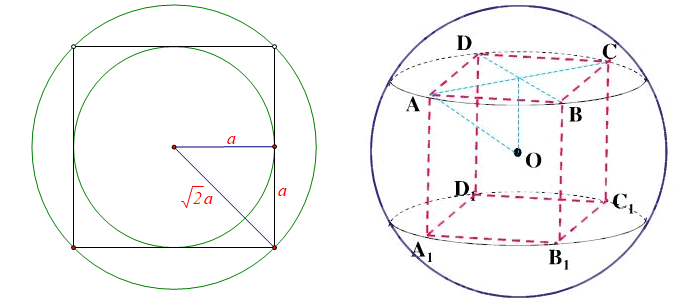
- (2)正方形的棱长设为(2a),则正方形的内切圆半径为(a),正方形的外接圆半径为(sqrt{2}a),三者的关系之比为(2:1:sqrt{2});
正方体的棱长设为(2a),则正方体的内切球半径为(a),正方体的外接球半径为(sqrt{3}a),三者的关系之比为(2:1:sqrt{3});
- (3)正三角形的棱长设为(2a),则正三角形的内切圆半径为(cfrac{sqrt{3}}{3}a),正三角形的外接圆半径为(cfrac{2sqrt{3}}{3}a),三者的关系之比为(2sqrt{3}:1:2);
正四面体的棱长设为(2a),则正四面体的内切球半径为(cfrac{sqrt{6 }}{6}a),正四面体的外接球半径为(cfrac{sqrt{6 }}{2}a),三者的关系之比为(2sqrt{6}:1:3);
(x+cfrac{1}{x}ge 2);
(x+cfrac{4}{x^2}=cfrac{x}{2}+cfrac{x}{2}+cfrac{4}{x^2}ge 3);
(x+cfrac{27}{x^2}=cfrac{x}{3}+cfrac{x}{3}+cfrac{x}{3}+cfrac{27}{x^3}ge 4);
(cdots),类比得到
(x+cfrac{a}{x^n}ge n+1),则(a)=__________。
分析:第一个式子是(n=1)的情形,此时(a=1^1=1);
第二个式子是(n=2)的情形,此时(a=2^2=4);
第三式子是(n=3)的情形,此时(a=3^3=27);
归纳可知, (a=n^n);
延伸阅读:上述表达式其实是均值不等式的拓展情形,
二元均值不等式:(x+cfrac{1}{x}ge 2sqrt{x imes cfrac{1}{x}}=2);
三元均值不等式:(x+cfrac{4}{x^2}=cfrac{x}{2}+cfrac{x}{2}+cfrac{4}{x^2}ge 3sqrt[3]{cfrac{x}{2} imescfrac{x}{2} imescfrac{4}{x^2}}=3);
四元均值不等式:(x+cfrac{27}{x^2}=cfrac{x}{3}+cfrac{x}{3}+cfrac{x}{3}+cfrac{27}{x^3}ge 4sqrt[4]{cfrac{x}{3} imescfrac{x}{3} imescfrac{x}{3} imescfrac{27}{x^3}}=4);
对于半径为(R)的球,若将(R)看作((0,+infty))上的变量,类比圆的上述性质,可得球的相关性质为________________________(语言叙述).
分析:半径为(R)的球体积(V= cfrac{4}{3}pi R^3),表面积(S=4pi R^2),显然$ (cfrac{4}{3}pi R^3)′=4pi R^2$,
即球的体积函数的导数等于球的表面积函数。
- 已知等差数列({a_n})中,(cfrac{a_{11}+a_{12}+cdots+a_{20}}{10}=cfrac{a_1+a_2+cdots+a_{30}}{30}),
则在等比数列中:(sqrt[10]{b_{11}cdot b_{12}cdots b_{20}}=sqrt[30]{b_1cdot b_2cdots b_{30}})。
- 由圆(x^2+y^2=r^2)的面积(S=pi r^2),类比得到
椭圆(cfrac{x^2}{a^2}+cfrac{y^2}{b^2}=1)的面积(S=pi ab)。
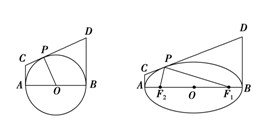
分析:椭圆中的焦半径类比圆中的半径,有(PF_1cdot PF_2=PCcdot PD)
提示:左图中结论的证明,连结(OC),(OD),利用射影定理证明。
参考上述解法,若关于(x)的不等式(cfrac{k}{x+a}+cfrac{x+b}{x+c}<0)的解集为((-1,-cfrac{1}{3})cup(cfrac{1}{2},1)),则关于(x)的不等式(cfrac{kx}{ax+1}+cfrac{bx+1}{cx+1}<0)的解集为________.
分析:本题目对学生的思维的灵活性要求比较高,需要有一定的数学素养的储备。
关于(x)的不等式(cfrac{k}{x+a}+cfrac{x+b}{x+c}<0)的解集为(xin (-1,-cfrac{1}{3})cup(cfrac{1}{2},1)),
所以用(cfrac{1}{x})代换解集中的(x),(-1<cfrac{1}{x}<-cfrac{1}{3})或者(cfrac{1}{2}<cfrac{1}{x}<1),可得(-3<x<-1)或(1<x<2),
用(cfrac{1}{x})代换原不等式中的(x),即为(cfrac{k(cfrac{1}{x})}{a(cfrac{1}{x})+1}+cfrac{b(cfrac{1}{x})+1}{c(cfrac{1}{x})+1}<0)的解集为(-3<x<-1)或(1<x<2),
即就是(x)的不等式(cfrac{kx}{ax+1}+cfrac{bx+1}{cx+1}<0)的解集为(-3<x<-1)或(1<x<2)。
感悟思考:本题目的求解不是常规的求各个系数的值,然后按照常规解不等式,而是巧妙运用代换法求解,即将解集代换,将不等式代换。
于此类似的有下列问题,
如已知(f(x)+2f(-x)=2x+3),求(f(x))的解析式;
再如已知(3f(x)+f(cfrac{1}{x})=x),求(f(x))的解析式。