GAN的数学原理

信息论基础

信息论的基本想法 - 如何量化信息？

• 非常可能发生的事件信息量较少，确保能够发生的事件应该没有信息量。
• 较不可能发生的实践具有更高的信息量。
• 独立事件应具有增量的信息。例如，投掷的硬币两次正面朝上传递的信息量，应该是投掷一次硬币正面朝上的信息量的两倍。

为了满足上述三个性质，定义一个事件(X=x)的自信息为

[I(x)=-logP(x) ]

其中(P(x))为观察到该事件的概率。

自信息只能处理单个的输出。可以用香农熵(Shannon entropy)来对整个概率分布中的不确定性总量进行量化：

[H(X)=mathbb E_{xsim P}[I(x)]=-mathbb E_{xsim P}[logP(x)] ]

一个分布的香农熵是指遵循这个分布的事件所产生的期望信息总量，它给出了对依据概率分布(P)生成的符号进行编码所需的比特数在平均意义上的下界(当对数底数不是 2 时，单位将有所不同)。

可以将问题理解为给一些字符编码，这些字符出现的频率不同，我们给那些出现频率高的字符，优先赋予较短的编码，给那些出现频率低的字符，赋予稍长一些的编码，这个问题可以用数据结构中的哈弗曼树解决，(-logP(x))可以理解为在这种策略下，赋予字符(x)的编码长度。

如果我们对于同一随机变量(X)有两个单独的概率分布(P(x))和(Q(x))，我们可以使用KL散度(Kullback-Leibler divergence)来衡量这两个分布的差异：

[D_{KL}(P||Q)=mathbb E_{xsim P}Big[logfrac{P(x)}{Q(x)}Big]=-mathbb E_{xsim P}[logQ(x)]-ig(-mathbb E_{xsim P}[logP(x)]ig) \=-mathbb E_{xsim P}[logQ(x)]-H(P) ]

KL 散度衡量的是，当我们使用一种被设计成能够使得概率分布 Q 产生的消息的长度最小的编码（记为BQ），发送包含由概率分布 P 产生的符号的消息时，多发送的消息长度，这里的多是相对于使用能够使得概率分布 P 产生的消息的长度最小的编码（记为BP）。

因为消息是以概率P发送的，所以使用编码BP才能使消息长度最短，使用编码BQ会多发送一些比特，KL散度衡量的就是多发送的比特长度。所以我们很容易知道KL散度是非负的，KL 散度为 0 当且仅当P 和 Q 在离散型变量的情况下是相同的分布，或者在连续型变量的情况下是几乎处处相同的。

一个和 KL 散度密切联系的量是交叉熵(cross-entropy)，

[H(P,Q)=H(P)+D_{KL}(P||Q)=-mathbb E_{xsim P}[logQ(x)] ]

针对 Q 最小化交叉熵等价于最小化 KL 散度，因为 Q 并不参与被省略的那一项。在机器学习分类任务中，Q为神经网络学习到的分布，P为数据真实分布，(P(x))的取值只有1（正确分类）和0（错误分类）两种可能，所以

[H(P)=-mathbb E_{xsim P}[logP(x)]=-sum_xP(x)logP(x)=0 ]

恒成立，即交叉熵的值与KL散度相等（信息论中，0log0=0）。

GAN之前，如何寻找数据的分布？

假设我们想找到一个数据分布(P_{data}(x))，使一张图片看起来像是二次元头像，其中(x)是一个高维向量，代表一张图片。在整个向量空间中，只有一小部分空间中的向量所代表的图片像是二次元头像，比如下图中的蓝色区域

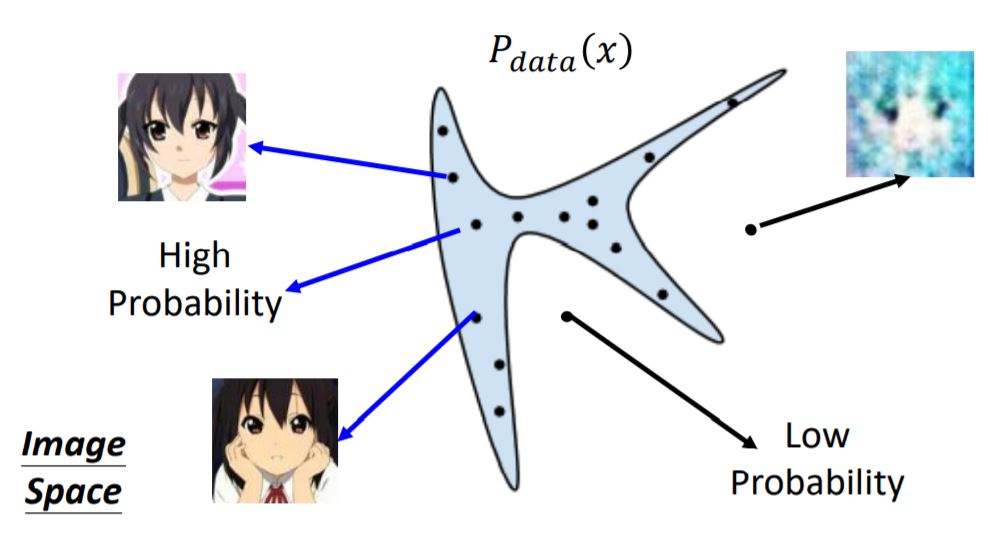
我们所要寻找的分布(P_{data}(x))，应该在蓝色区域概率高，在其他区域概率低。
在GAN之前，我们使用的是最大似然估计方法：

• 给定一个真实数据分布(P_{data}(x))，并且我们可以从中抽样
• 假设一个数据分布(P_G(x; heta))，其中( heta)为参数（如果假设为高斯分布，( heta)就是分布的均值与方差）
• 寻找使(P_G(x; heta))最接近(P_{data}(x))的参数( heta)
• 从(P_{data}(x))中抽样得到({x^1,x^2,dots,x^m})，我们可以计算出从(P_G(x; heta))中抽样得到这些样本的概率(P_G(x^i; heta))
• 似然函数(L=prod limits ^m _{i=1} P_G(x^i; heta))
• 寻找( heta^*)使L最大

我们对( heta^*)进一步计算：

[ heta^*=argmaxlimits_ hetaprod limits ^m _{i=1} P_G(x^i; heta) =argmaxlimits_ heta logprod limits ^m _{i=1} P_G(x^i; heta) \=argmaxlimits_ hetasum limits ^m _{i=1} logP_G(x^i; heta) ]

我们假设样本({x^1,x^2,dots,x^m})的分布与(P_{data}(x))的分布几乎一致，并且把(sum limits ^m _{i=1} logP_G(x^i; heta))理解为m倍的数学期望，那么

[argmaxlimits_ hetasum limits ^m _{i=1} logP_G(x^i; heta) approx argmaxlimits_ hetamathbb E_{xsim P_{data}}[logP_G(x^i; heta)]\=argminlimits_ heta H(P_{data},P_G)=argminlimits_ heta D_{KL}(P_{data}||P_G) ]

所以，求参数( heta)使似然函数最大，就是使交叉熵与KL散度最小，由上节内容可知，这就是使两个概率分布最相似。
上述做法有一个无法解决的问题，那就是数据的分布很可能不是高斯分布，而是极其复杂、很难预估的分布，我们无法提前写出(P_G(x; heta))的表达式，这时我们只能用神经网络来表示它。

生成对抗网络

生成器G是一个神经网络，它定义了一个概率分布(P_G)，由于神经网络可以近似任意函数，所以无论目标概率分布多复杂，我们都可以近似它。

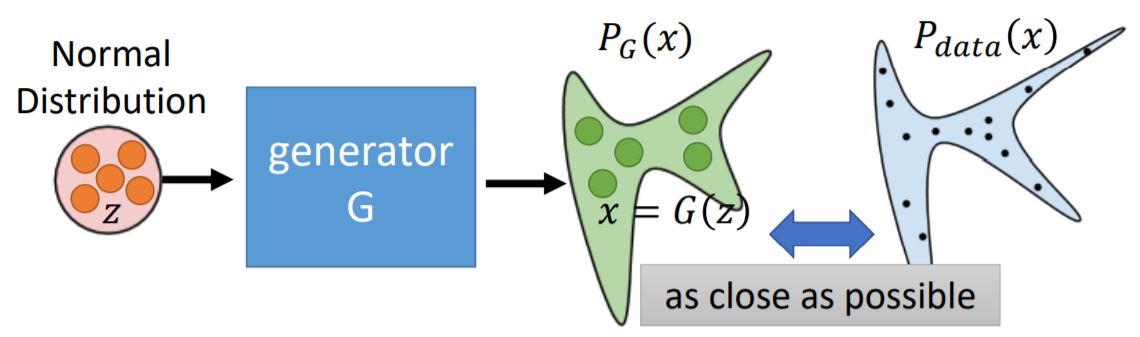
此时我们要寻找的生成器(G^*=argminlimits_GDiv(P_G,P_{data}))

那么，如何计算(Div(P_G,P_{data}))，即两个分布的差异呢？

鉴别器D同样是一个神经网络，将生成器生成的样本与真实数据作为训练样本，输入D中，D的输出为(D(x))，

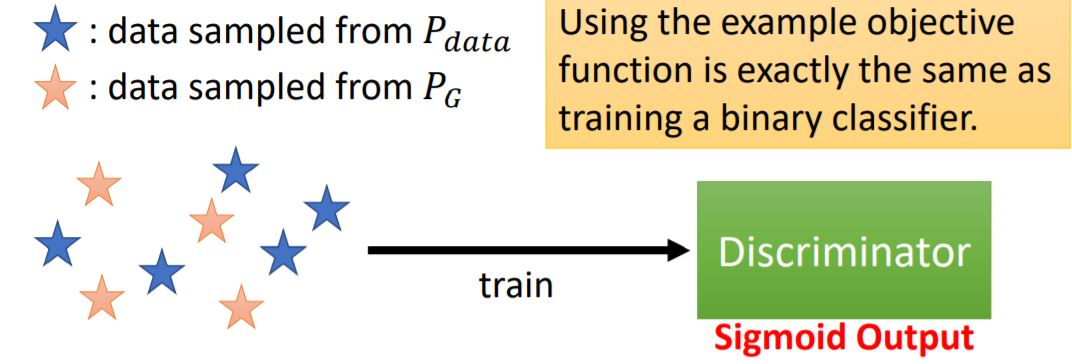
设目标函数

[V(G,D)=mathbb E_{xsim P_{data}}[logD(x)]+mathbb E_{xsim P_G}[log(1-D(x))] ]

我们要寻找的鉴别器(D^*=argmaxlimits_DV(D,G))，给定(G)，(D^*)可以最大化

[V=mathbb E_{xsim P_{data}}[logD(x)]+mathbb E_{xsim P_G}[log(1-D(x))] \=intlimits_x[P_{data}(x)logD(x)+P_G(x)log(1-D(x))]dx ]

即给定(x)，(D^*)可以最大化(P_{data}(x)logD(x)+P_G(x)log(1-D(x)))

设(f(D)=alog(D)+blog(1-D))，求极值点得(D^*=frac{a}{a+b})，即

[D^*=frac{P_{data}(x)}{P_{data}(x)+P_G(x)} ]

此时目标函数

[maxV(G,D)=V(G,D^*)=mathbb E_{xsim P_{data}}[logfrac{P_{data}(x)}{P_{data}(x)+P_G(x)}]+mathbb E_{xsim P_G}[log(frac{P_G(x)}{P_{data}(x)+P_G(x)})] \=-2log2+D_{KL}Big(P_{data}||frac{P_{data}+P_G}{2}Big)+D_{KL}Big(P_G||frac{P_{data}+P_G}{2}Big) \=-2log2+2D_{JS}(P_{data}||P_G) ]

与两个分布的JS散度正相关。

回到前面的问题，目标函数可以衡量两个分布的JS散度（差异度），所以(G^*=argminlimits_Gmaxlimits_DV(G,D))，

• 步骤1：固定生成器G，更新鉴别器D使目标函数最大
• 步骤2：固定鉴别器D，更新生成器G使目标函数最小

以上三个生成器中，(G_3)是最优的。

GAN的算法

一个问题是，为什么在一次训练迭代中，D迭代的次数比G多？
若G迭代次数过多，会使D陷入局部最优，如下图：

• 表面上，由于G的更新，找到了更小的(maxlimits_DV(G,D))，但此时G已经变为了(G_1)，非常不幸的是，上文已经说过，在G的更新过程中，D是被固定的；也就是说，此时(G_1=argminlimits_GV(G_1,D_0))，而(D_0 eq argmaxlimits_DV(G_1,D))；为了解决这个问题，我们必须假设(G_0approx G_1)，而这要求(G)的更新不能过于频繁。同时，若(G)更新过于频繁，会产生过拟合，对于不同的输入(z)，生成器只会产生最讨好(D)的那个输出，破坏了模型的多样性。
• 但若频繁更新(D)，同样会使鉴别器过拟合，此时任何生成器的输出都不能满足(D)，使优化更困难。

综合起来，(G)的迭代次数不能多于(D)，同时两者都不能在一个训练迭代中循环太多次。