在上一节中主要介绍了监督学习中的线性回归(模型)、最小二乘法(策略)、梯度下降法(算法)及线性最小二乘法的标准方程(闭式解)。
这节主要介绍两个回归:局部加权回归与逻辑回归,其中穿插一些小的知识点:欠拟合与过拟合、感知机、牛顿方法等。大纲如图:

一、几个概念
1. 欠拟合与过拟合问题

![]()
之前所采用的线性回归方法面对上图中的散点会用一条直线去拟合,并不是所有散点都大致分布在直线相同的距离处,很显然效果并不是很好,这种现象叫做“欠拟合”。

![]()
当加入一个x二次方的项时(x=size,房屋的长,x的二次方可以理解为size的平方,即房屋面积),从上图可以看出,有更多的散点落在了曲线上,拟合效果有所改善。随着特征的增加,曲线的拟合效果看似也随之增强,但事实上并非如此。

![]()
当特征的个数增加到五个时,曲线已经可以非常完美的拟合所有的散点,但是这样会导致检验样本必须完全符合训练样本集,也大大增加了系统的复杂性,这种现象叫做“过拟合”。
2. 参数化与非参数学习算法
(1)参数学习算法(Parametric Learning Algorithm)
有固定数目的参数以用来数据拟合的算法,如线性回归。
在线性回归模型中,首先,θ是和特征数目相同的固定数目参数;其次,一旦训练出模型后,θ的值就是固定的,在之后的预测过程中,不需要再使用训练样本集。
(2)非参数学习算法(Non-parametric Learning Algorithm)
参数的数目会随着训练集合的大小线性增长,如局部加权回归。
在局部加权回归模型中,每当需要预测时都会重新训练样本集,而每次训练所得到的θ可能是不同的,故θ的数目与值是不固定的。
二、局部加权回归
1. 模型假设:
- 线性回归模型的假设为:

- 局部加权回归的假设为:

其中,权重w的一个标准选择为:

w的表达函数其实是一个钟形函数,参数滔表示波长,控制权值随距离下降的速率。
对比后可以看出,在线性回归中误差函数的系数是1,没有赋予不同的权值。加入权重的线性回归模型就引申出局部加权回归模型。
2. 模型思路:
单看假设中的第一个式子,当w的值很大,就会使后面的方差因子更小;当w的值很小,就会忽略该项后面的方差因子,也就是只考虑到权重大的方差因子项的影响。
进一步地考察w的表达式,当xi与x的绝对值(xi与x的距离)很小时,w的值近似为1;当xi与x的绝对值很大时,w的值近似为0,可以理解为当查询一个确定的点x时(查询新的特征),给离得近的点(样本)赋予较大的权值,给离得远的点赋予较小的权值。
因此,局部加权回归模型的基本思路:通过拟合一组参数向量,更注重对临近点的精确拟合,同时忽略那些离得很远的点的贡献。
三、逻辑回归
1. 模型思路:
回归一般并不用在分类问题上,因为回归是连续型的模型,受噪声影响比较大。如果说可以用在分类上的回归,就是逻辑回归。
逻辑回归的本质是线性回归,为了解决分类问题(这里假设二值分类问题,即将特征通过方程映射到0和1两个值上),在特征到结果的映射中加入了一个函数映射g,即先将特征线性求和得到z,再通过函数g(z)映射到结果空间[0,1]。
逻辑回归的假设函数h:
![]()
g(z)也叫做Sigmoid函数:
![]()
它的导数也具有特殊形式:


2. 模型的解:
(1)梯度上升法
假设二值满足伯努利分布:

更一般的表示:
![]()
于是参数θ的似然函数(likelihood)为:

θ的log似然函数(log likelihood)为:
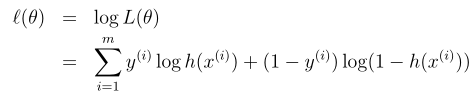
那么,如何来求解最大似然函数中的参数θ呢?可以参考线性回归的梯度下降法求解最小值的思路,不过不同的是这里求解的是最大值,在更新参数θ时按照梯度方向进行增长即可,也就是梯度上升法。
针对一个训练样本(x,y),参考随机梯度下降法的求解过程,结合g(z)函数导数的特殊性质,可以得到梯度上升法的解。


可以看出它的形式与随机梯度下降法十分相似,但是这里的h函数是非线性的Sigmoid函数。
(2)牛顿法
牛顿法是另一种求似然函数极大值的方法。它的本质是通过f(θ)=0确定下一个取斜率的点坐标,依次下去可以快速找到斜率为0时的极值。
参数θ的求解方程:


回归到求似然函数的极大值问题,类比上述思想可以推理出这里要求l(θ)导数为0的情况,即:

同理可得此时的参数估计为:

由于在逻辑回归中的参数θ是一个向量,因此我们需要扩展θ的参数估计。

H叫做Hessian,是一个nXn的矩阵。

牛顿方法比Batch梯度下降法的速度快得多,且迭代次数也少很多。只要样本个数n取值比较合理,它的收敛速度还是十分可观的。
三、感知机学习算法
逻辑回归中的Sigmoid函数“迫使”特征的线性之和映射到0或1,如果换一个函数,如阈值函数g(z):

同样会得到一个类似逻辑回归的随机上升梯度的解,只是h函数的映射有所不同。


于是就得到了感知机学习算法,它是学习理论的基础。
参考文献: