1. 01背包
状态转移方程
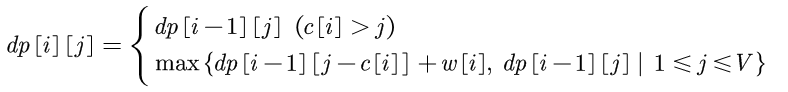
int dp[MA][MA]; int v[mA],w[MA]; for(int i=1;i<=n;i++) { for(int j=0;j<=V;j++) { if(j<v[i]) dp[i][j]=dp[i-1][j]; else dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]); } }
优化代码
dp[MA]={0};
for(int i=1;i<=n;i++) {
for(int j=V;j>=v[i];j--){ // 剩余空间 j 肯定要比当前费用大 ,逆序
dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
}
}
2.完全背包
状态转移方程
F[i,j]=max{F[i-1,j],F[i-1,j-k*wi]+k*vi}
int dp[MA][MA];//初始化为0 for(int i=1;i<=n;i++){ for(int j=0;j<V;j++){ for(int k=0;k*v[i]<=j;k++){ dp[i][j]=max(dp[i-1][j],dp[i-1][j-k*v[i]]+k*w[i]); } } }
优化代码(和01背包不同的是 第二行循环为顺序,因为要不断更新dp[j]
dp[MA]; for(int i=1;i<=n;i++){ for(int j=v[i];j<=V;j++){ //顺序 dp[j]=max(dp[j],dp[j-v[i]]+w[i]); } }
3. 01背包 完全背包 恰好装满问题(这就是初始值的问题)
是否恰好装满的解法不同只在于初始值的不同
恰好装满:
求最大值时,除了dp[0] 为0,其他都初始化为无穷小 -0x3f3f3f3f
求最小值时,除了dp[0] 为0,其他都初始化为无穷大 0x3f3f3f3f
不必恰好装满:
全初始化为0
why: dp数组的初始化的含义是当背包容量为 j 时,没有任何物品放入背包时的合法状态
- 当不必恰好装满时,对任意dp[ j ] 在没有物品放入时 价值最大值 都为0;
- 当恰好装满时,(求最大价值)dp[0] 肯定为 0,其为背包容量为0的合法状态,除此以外dp[ j ] 都为 负无穷,因为背包容量>0 在不装物品时无法装满,且求最大值需要进行max()比较,一旦有合法状态成立就改变 dp[ j ] 的值,因此初始化为 负无穷
- 同理 恰好装满 ,求 最小值 ,需要进行 min() 比较,初始化为 无穷大
4.最长上升子序列
状态转移方程
int ans=-1; for(int i=0;i<n;i++){ a[i].dp=1; for(int j=i;j>=0;j--){ if(a[j].x<a[i].x){ a[i].dp=max(a[i].dp,a[j].dp+1); } } ans=max(a[i].dp,ans); }
5. 最长公共子序列
#include<iostream> using namespace std; const int MA=1005; int dp[MA][MA]={0}; string a,b; int main(){ cin>>a>>b; int n=a.size(); int m=b.size(); a=' '+a; b=' '+b; for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ if(a[i]==b[j])dp[i][j]=dp[i-1][j-1]+1; else dp[i][j]=max(dp[i][j-1],dp[i-1][j]); } } cout<<dp[n][m]<<endl; return 0; }