某天,老师向我们讲了“最大连续子序列”,结果居然越讲越奇葩深入,特此记下:
线性结构(一维)
Problem:
设数组a是一个有n个元素的整数数组a1,a2,a3,a4……an ,从中找出最大和的连续子序列。
【输入格式】
包括2行:第一行一个正整数N(1≤=N≤1000),表示数组序列元素个数,第二行为连续的N个整数,描述这个序列。
【输出格式】
输出包括2行,第一行为和最大的子序列,第二行,只有一个正整数,为最大和。
【输入样例】
10
10 -29 30 24 40 -100 80 120 20 -50
【输入样例】
80 120 20
220
Answer 1:暴力枚举无敌~
连续序列的左端点st从1到n枚举,右端点ed从st到n枚举,连续序列st到en的长度也是从1到n枚举,所以此算法时间复杂度是O(n^3)。
程序
#include<iostream>
using namespace std;
int a[10001];
int st,en,n,max0,sum0;
int main()
{
cin>>n;
max0=-0xfffffff;
for(int i=1;i<=n;i++)
cin>>a[i];
for(int i=1;i<=n;i++)
for(int j=i;j<=n;j++)
{
sum0=0;
for(int k=i;k<=j;k++)
sum0=sum0+a[k];
if(sum0>max0)
{
max0=sum0;
st=i;
en=j;
}
}
for (int i=st;i<=en;i++)
cout<<a[i]<<" ";
cout<<max0;
return 0;
}
Answer 2:前缀和
之前总觉得前缀和很难,现在一看其实也很简单哒。复杂度O(n^2)。直接上程序喽
程序
#include<iostream>
using namespace std;
int a[10001],sum[10001];
int st,en,n;
long long max0;
int main()
{
cin>>n;
max0=-0xffffffff;
for (int i=1;i<=n;i++)
{
cin>>a[i];
sum[i]=sum[i-1]+a[i];
}
for (int i=1,t=0;i<=n;i++)
for (int j=i;j<=n;j++)
{
t=sum[j]-sum[i-1];
if (t>max0)
{
max0=t;
st=i;
en=j;
}
}
for (int i=st;i<=en;i++)
cout<<a[i]<<" ";
cout<<endl<<max0;
return 0;
}
Answer 3:二分
上面两种算法都是 朴素算法 ,枚举每个可能,从而找到最优的解。然而还有没有更优的解呢?答案依旧是肯定的。
我们不妨从小规模数据分析,当序列只有一个元素的时候,最大的和只有一个个可能,就是选取本身;当序列有两个元素的时候,只有三种可能,选取左边元素、选取右边元素、两个都选,这三个可能中选取一个最大的就是当前情况的最优解;对于多个元素的时候,最大的和也有三个情况,从左区间中产生、从右区间产生、左右区间各选取一段。因此不难看出,这个算法是基于分治思想的,每次二分序列,直到序列只有一个元素或者两个元素。当只有一个元素的时候就返回自身的值,有两个的时候返回3个中最大的,有多个元素的时候返回左、右、中间的最大值。然后,将3种情况的最大子段和合并,取三者之中的最大值为问题的解。因为是基于二分的思想,所以时间效率能达到O(nLogn)。
程序
#include<iostream>
using namespace std;
int n,a[1000001];
int MAxSubSum(int left,int right)
{
int sum=0;
if (left==right)
sum=a[left]>0?a[left]:0;
else
{
int center=(left+right)/2;
int leftsum=MAxSubSum(left,center);
int rightsum=MAxSubSum(center+1,right);
int s1=0;
int lefts=0;
for(int i=center;i>=left;i--)
{
lefts+=a[i];
if(lefts>s1) s1=lefts;
}
int s2=0;
int rights=0;
for(int i=center+1;i<=right;i++)
{
rights+=a[i];
if(rights>s2) s2=rights;
}
sum=s1+s2;
if(sum<leftsum) sum=leftsum;
if(sum<rightsum) sum=rightsum;
}
return sum;
}
int main(){
cin>>n;
for (int i=1;i<=n;i++) cin>>a[i];
cout<<MAxSubSum(1,n);
return 0;
}
Answer 4:重磅嘉宾:动态规划!
设计一个数组f,f[i]表示前i个元素能组成的最大和。如果f[i-1]大于零,则不管a[i]的情况,f[i-1]都可以向正方向影响a[i],因此可以将a[i]加在f[i-1]上。如果f[i-1]小于零,则不管a[i]再大,都会产生负影响,因此我们还不如直接令f[i]=a[i]。因此状态转移方程就在这里。我们只需在f中扫描一次,找到最大的值就是最大子段的和,复杂度为O(n)!
程序
#include<iostream>
using namespace std;
int n,a[1000001],f[1000001];
long long sum0;
int main()
{
cin>>n;
for (int i=0;i<n;i++)
cin>>a[i];
f[0]=0;
sum0=0;
for (int i=1;i<n;i++)
{
if (f[i-1]+a[i]>a[i]) f[i]=f[i-1]+a[i];
else f[i]=a[i];
if (f[i]>sum0) sum0=f[i];
}
cout<<sum0;
return 0;
}
一维空间已突破,正在进入二维空间
接下来我们来看平面结构:最大加权矩阵(二维)
Problem:
给定一个正整数n( n<=100),然后输入一个N*N矩阵。求矩阵中最大加权矩形,即矩阵的每一个元素都有一权值,权值定义在整数集上。从中找一矩形,矩形大小无限制,是其中包含的所有元素的和最大 。矩阵的每个元素属于[-127,127]
【输入格式】
第一行:n,接下来是n行n列的矩阵。
【输出格式】
一个整数,即最大矩形(子矩阵)的和。
【输入样例】
4
0 –2 –7 0
9 2 –6 2
-4 1 –4 1
–1 8 0 –2
【输入样例】
15
【样例解析】
9 2
-4 1
-1 8
和为15
Answer 1:还是暴力枚举!
两个维度分别枚举,如下图,直接枚举矩阵的左上角和右下角坐标。But……这次的时间复杂度变成了O(n^6)!恐怖如斯
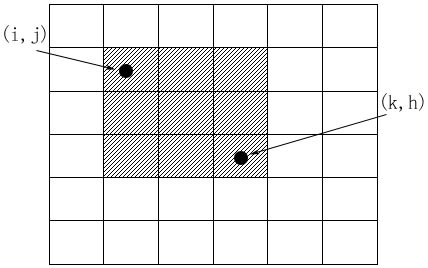
代码
#include<iostream>
using namespace std;
int v,n,a[10007][10007];
int maxn,stx,sty,eny,enx;
int main()
{
cin >> n;
maxn=-0xfffffff;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
cin >> a[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=i;k<=n;k++)
for(int h=j;h<=n;h++)
{
v=0;
for(int e=i;e<=k;e++)
for(int f=j;f<h;f++)
v+=a[e][f];
if(v>maxn)
{
maxn=v;
stx=i;
enx=k;
sty=j;
eny=h;
}
}
cout << maxn;
return 0;
}
当然,仅仅O(n^6)得时间复杂度是满足不了我们的,于是——
Answer 2:二维前缀和
那……这怎么做呢?细想一下,其实也不难,就像这道小学数学题:
……或者这几道:
(图片来源于网络,侵删)
所以,详细步骤就是这样:
- 引入数组sum[i,j],代表下图中阴影部分a数组区域和。即点[1,1]为左上角到[i,j]为右下角的矩形区域的加权和。

- 根据下图可以得出下面公式:sum[i,j]= sum[i-1,j]+ sum[i,j-1]- sum[i-1,j-1]+a[i,j]
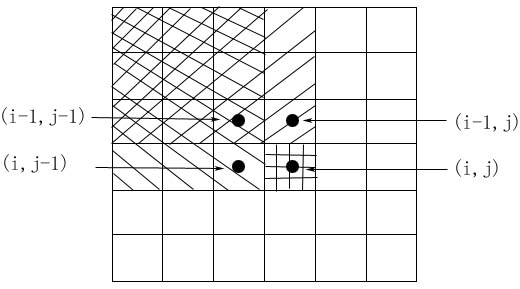
- 继续可以得到这个公式:即点(i,j)到点(k,h)的矩阵中值的和为:sum[k,h]- sum[i-1,h]- sum[k,j-1]+ sum[i-1,j-1]
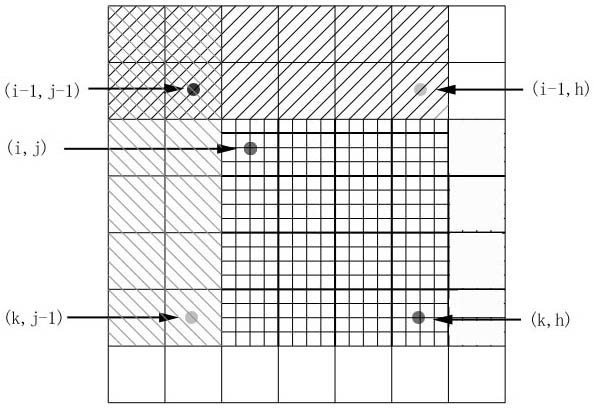
再联系那几道小学数学题理解一下,是不是简单多了?
于是乎……时间复杂度变为了O(n^4)~