蓝桥杯试题历届试题包子凑数 dp+欧几里得算法

问题描述

　　小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼，其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼，可以认为是无限笼。

　　每当有顾客想买X个包子，卖包子的大叔就会迅速选出若干笼包子来，使得这若干笼中恰好一共有X个包子。比如一共有3种蒸笼，分别能放3、4和5个包子。当顾客想买11个包子时，大叔就会选2笼3个的再加1笼5个的（也可能选出1笼3个的再加2笼4个的）。

　　当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有3种蒸笼，分别能放4、5和6个包子。而顾客想买7个包子时，大叔就凑不出来了。

　　小明想知道一共有多少种数目是包子大叔凑不出来的。

输入格式

　　第一行包含一个整数N。(1 <= N <= 100)
　　以下N行每行包含一个整数Ai。(1 <= Ai <= 100)

输出格式

　　一个整数代表答案。如果凑不出的数目有无限多个，输出INF。

样例输入

2
45
5

样例输出

样例输入

2
4
6

样例输出

INF

样例说明

　　对于样例1，凑不出的数目包括：1, 2, 3, 6, 7, 11。
　　对于样例2，所有奇数都凑不出来，所以有无限多个。

解题思路：我们首先观察第一个样例

×表示不能凑出，√表示能凑出。观察到8√可以从4√+4得到，10√可以从5√得到。

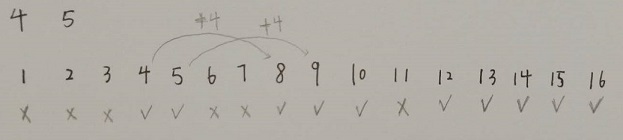
所以我们得出判断一个包子数是否能凑出的一个方法:dp解决。设dp[ j ]表示包子数为j是否能凑出。

有 dp[ j ] |= dp[ j - A[ k ] ] ( k>0 && j - A[k] >=0 )

进一步观察可以知道,当连续√的数目>=4时，之后的数目都一定能凑出，因为只要在之前√的基础上加上最小包子数4即可。

接着观察第二个样例: 4 6 最后样例输出是INF。这里可以证明只有当给出的包子数至少有两个互质时最终结果不是INF。

　　反证法:假设n个包子数都不互质，则它们的最小公约数k>1,则它们可以表示为

　　ka1,ka2,ka3, .... kan,则相加结果为 k( c1*a1 + c2 * a2 + ... + cn*an ) , 那么当要凑出的数不是k的倍数的时候，一定凑不出。

　　而不是k倍数的包子数有INF个.

要判断两个数是否互质，则要计算两个数的最大公约数是否为1，用到了辗转相除法，附上大佬详细证明 https://www.cnblogs.com/frog112111/archive/2012/08/19/2646012.html
而这里dp数组的大小与两个数最大不能组合的数有关.m,n（前提为互质）最大不能组合的数可以证明是 m*n - m -n 有兴趣的朋友可以看https://www.cnblogs.com/DestinHistoire/p/10632970.html

根据上面思路写的代码提交错了一题，输入96，75，100按照思路结果应该是INF，但仔细想想

ka1 + ka2 + ka3 +...+ ka4 = gcd( a1,a2,...,an) 的倍数,所以只需要所有包子数的公约数>1即可。(拓展欧几里得：

核心思想：考虑 a1*x1+a2*x2+...+an*xn=gcd(a1,a2,...an),只能凑出来gcd的倍数)

实现代码：

#include<cstdio>
#include<algorithm>
using namespace std;

const int Max_N = 100;
const int Max_K = 10000;//最大不能组合的数不会超过100*100

//输入
int N;
int A[Max_N];

bool dp[Max_K+1];//dp[] 全局变量初值为false 当然最好使用前初始化 

//辗转相除法 
int gcd(int a,int b)
{
    return a%b==0 ? b : gcd(b,a%b);
} 

void solve()
{
    //先判断是否为INF 
    int k = A[0];
    for( int i=1; i<N; i++)
    {
        k = gcd( k, A[i] );//求所有包子数的最大公约数 
    }
    if( k>1 ){
        printf("INF
");
        return;
    }
    
    sort(A,A+N);
    dp[0] = true;
    for(int i=1; i<=Max_K; i++)
    {
        for(int k=0; k<N&&A[k]<=i; k++)
        {
            if( dp[ i-A[k] ] )
            {
                dp[i] = true;
                break;
            }
        }
    }
    
    int ans=0, cnt = 0;
    for(int i=1; i<=Max_K; i++)
    {
        if( dp[i] )
        {
            cnt++;
            if( cnt==A[0] )    break;//连续√ 
        }
        else
        {
            cnt = 0;
            ans++;//不能凑的包子数    
        } 
    }
    printf("%d
",ans);
}

int main()
{
    scanf("%d",&N);
    for(int i=0; i<N; i++)
    {
        scanf("%d",&A[i]); 
    }
    
    solve();
    
    return 0;
}

蓝桥杯 试题 历届试题 包子凑数 dp+欧几里得算法

蓝桥杯试题历届试题包子凑数 dp+欧几里得算法