1.朴素贝叶斯的使用条件

朴素贝叶斯方法假设条件概率分布是相互独立的,这个假设会使每个属性独立的对分类结果产生影响

因此，根据独立性有，$p(x_1,x_2,...,x_n|C) = p(x_1|C)p(x_2|C)...p(x_n|C)，其中x_n是特征，C是分类的类别$

2.贝叶斯公式

由于朴素贝叶斯假设属性之间相互独立，所以贝叶斯公式可以写成如下形式

$p(C|mathbf x) = {p(C) p(x_1,x_2,...,x_n | C)over p(x_1,x_2,...,x_n)} = {p(C) over p(x_1,x_2,...,x_n)} p(x_1 | C) p(x_2 | C) ldots p(x_n | C)$

1)训练数据集的n个特征为$x = (x_1,x_2,ldots,x_n)$

2)假设C代表分类的类别

分别计算概率$p(x_1 | C)， p(x_2 | C)， ldots ，p(x_n | C)$

计算$p(C)$

由于$p(x_1,x_2,...,x_n)$对于所有的C类来说都是一样的，所以可以把这一项看做常数，因此

$p(C|mathbf x) propto p(C) p(x_1 | C) p(x_2 | C) ldots p(x_n | C)$

其中 $propto$表示成比例关系，如y = kx可以写成$y propto x$

3)故要想使$p(C|mathbf x)$最大，即使$ p(C) p(x_1 | C) p(x_2 | C) ldots p(x_n | C)$最大

$hat C = argmax p(C) p(x_1 | C) p(x_2 | C) ldots p(x_n | C) $

判断$mathbf x = ${Outlook = Sunny，Temperature = Cool，Humidty = High，Wind = Strong}能不能打网球

Outlook{Sunny、Overcast、Rain}

Temperature{Hot、Mild、Cool}

Humidty{High、Normal}

Wind{Weak、Strong}

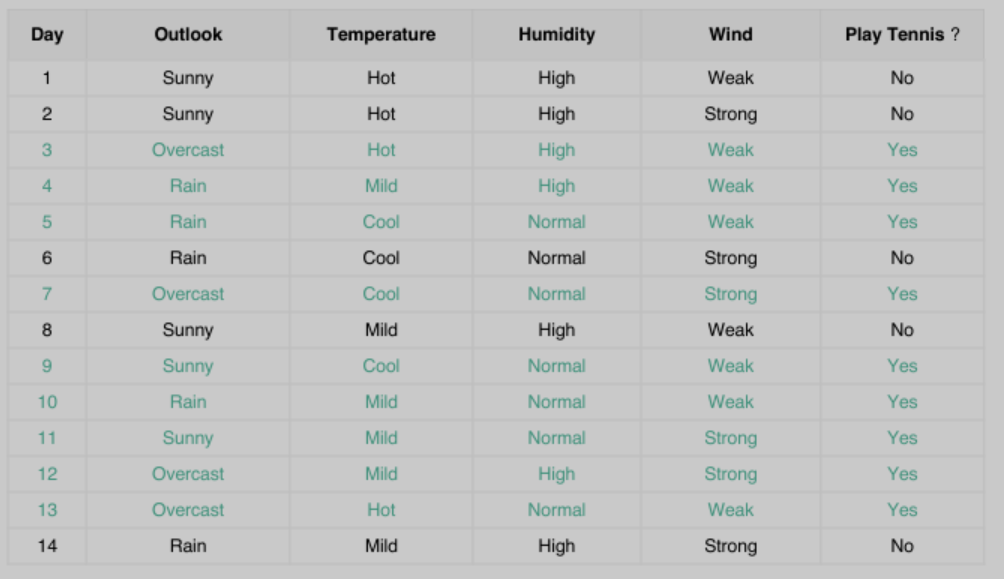
1）$x = (x_1,x_2,x_3,x_4)$，其中$x_1$是Outlook = Sunny、$x_2$是Temperature = Cool、$x_3$是Humidty = High、$x_4$是Wind = Strong

2）为了更直观的计算概率$p(x_1 | C)， p(x_2 | C)，p(x_3 | C) ，p(x_4 | C)$，将上表整理成如下形式，其中C是分类的类别Play = yes 或 Play = No

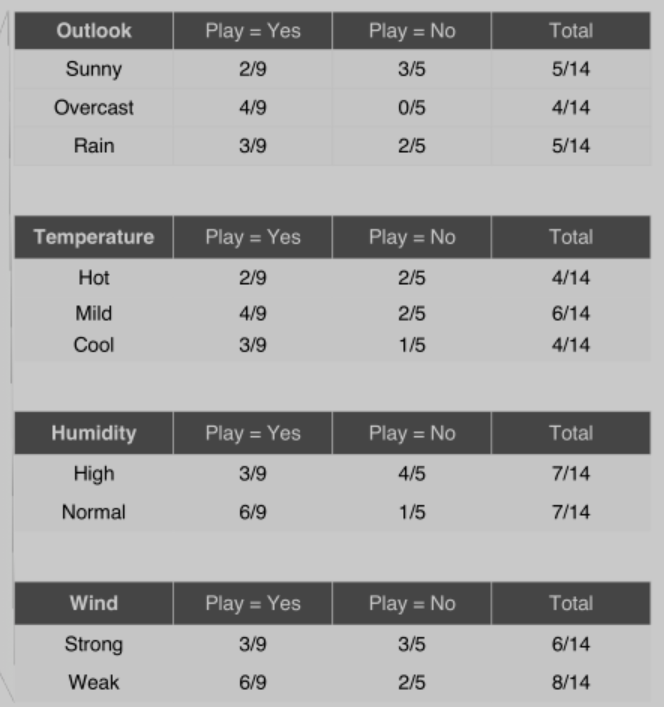
$p(x_1 | Play = yes) = {2over 9}$　　　　$p(x_1 | Play = No) = {3over 5}$

$p(x_2 | Play = yes) = {3over 9}$　　　　$p(x_2 | Play = No) = {1over 5}$

$p(x_3 | Play = yes) = {3over 9}$　　　　$p(x_3 | Play = No) = {4over 5}$

$p(x_4 | Play = yes) = {3over 9}$　　　　$p(x_4 | Play = No) = {3over 5}$

$p(Play = yes) = {9over 14}$　　　　　　$p(Play = yes) = {5over 14}$

3) $p(Play = yes) p(x_1 | Play = yes)p(x_2 | Play = yes)p(x_3 | Play = yes)p(x_4 | Play = yes) = 0.005$

$p(Play = No) p(x_1 | Play = No)p(x_2 | Play = No)p(x_3 | Play = No)p(x_4 | Play = No) = 0.02$

故$mathbf x = ${Outlook = Sunny，Temperature = Cool，Humidty = High，Wind = Strong}不能打网球