强化学习（八）：Eligibility Trace

Eligibility Traces

Eligibility Traces是强化学习中很基本很重要的一个概念。几乎所有的TD算法可以结合eligibility traces获得更一般化的算法，并且通常会更有效率。

Eligibility traces可以将TD和Monte Carlo算法统一起来。之前我们见过n-step方法将二者统一起来，eligibility traces 优于n-step的主要地方在于计算非常有效率，其只需要一个trace向量，而不需要储存n个特征向量。另外，eligibility trace的学习是逐步的，而不需要等到n-steps之后。

Eligibility traces机制是通过一个短期的向量得到的，这个向量称为eligibility trace (pmb{z_t} in R^d)。正好呼应算法中的权重向量(pmb{w_t}in R^d).　大致的思想是这样的：当权重向量的某些分量参与到估计价值当中，那么与之相对应的eligibility trace分量也会立即变化，然后变化会慢慢的消失。

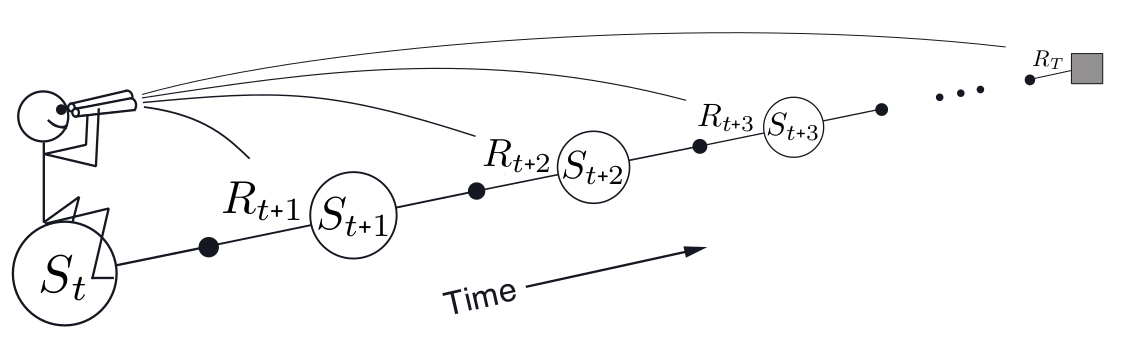
强化学习的很多算法都是‘向前看’的算法，即当前状态或动作的价值更新是依赖于未来状态或动作的，这样的　算法称为‘前向视角’。前向视角实施起来多少有些不方便，毕竟未来的事，当前并知道。还有另外一种思路是所谓的‘后向视角’，通过eligibility trace来考虑最近刚刚访问过的状态或动作。

The (lambda)-return

之前定义过n-steps return为最初n rewards加上n步之后的状态的价值估计的总和：

[G_{t:t+n} dot = R_{t+1} + gamma R_{t+2} + ... + gamma^{n-1}R_{t+n} + gamma^n hat v(S_{t+n}, w_{t+n-1}) ]

其实一个有效的更新不一定只依赖于n－steps return，可能依赖于多个n-step return的平均会更好，比如：

[frac{1}{2}G_{t:t+2} + frac{1}{2}G_{t:t+4} ]

(lambda)-return 可以理解为一种特殊的平均多个n-step return，它平均所有n-step return：

[G_{t}^{lambda}dot = (1- lambda)sum_{n=1}^{infty}gamma^{n-1}G_{t:t+n} = (1-lambda)sum_{n=1}^{T-t-1}lambda^{n-1}G_{t:t+n} + lambda^{T-t-1}G_{t} ]

基于(lambda) return 的学习算法比如off-line (lambda)－return algorithm:

[w_{t+1}dot = w_t + alpha [ G_t^{lambda} - hat v(S_t, w_t)] abla hat v(S_t,w_t), t = 0,..., T-1. ]

以上其实就是一种前向视角：

TD((lambda))

TD((lambda))是上面off-line (lambda)-return算法的改进，主要有三点：一是它每步更新，二是因为每步更新，它的计算过程分布在每一时间步上，三是它可以应用于连续过程而不仅限于episodic problems。

如上所述，eligibility trace　通过一个向量(pmb{z_t}in R^d) 实现，其与(pmb{w_t})维度相同，(pmb{w_t})可看作是长时记忆，而eligibility trace则是短时记忆。

[z_{-1}dot = 0, qquad z_tdot = gamma lambda z_{t-1} + ablahat v(S_t,w_t),qquad 0 le tle T ]

其中(gamma)是discount rate，(lambda) 是trace decay参数。Eligibility trace记录权重向量各成分在近期状态价值评估中的贡献。

TD error:

[delta_t dot = R_{t+1} +gammahat v(S_{t+1},w_t)- hat v(S_t,w_t) ]

那么权重向量的更新：

[w_{t+1} dot = w_t+alpha delta_t z_t ]

# semi-gradient TD(lambda) for estimating v_hat = v_pi
Input: the policy pi to be evaluated
Input: a differentiable function v_hat: S_plus x R^d --> R such that v_hat(terminal,.) = 0
Algorithm parameters: step size alpha > 0, trace decay rate lambda in [0,1]
Initialize value-function weights w arbitrarily (e.g. w = 0)
Loop for each episode:
    Initialize S
    z = 0
    Loop for each step of episode:
        Choose action A based on pi(.|S)
        Take A, observe R,S'
        z = gamma * lambda *z + grad V(S,w)
        delta = R + gamma v_hat(S',w) - v_hat(S,w)
        w = w + alpha delta z
        S = S'
    until S' is terminal

TD((lambda))是时间上反向的，从当前状态，向后考虑已经经历过的状态。

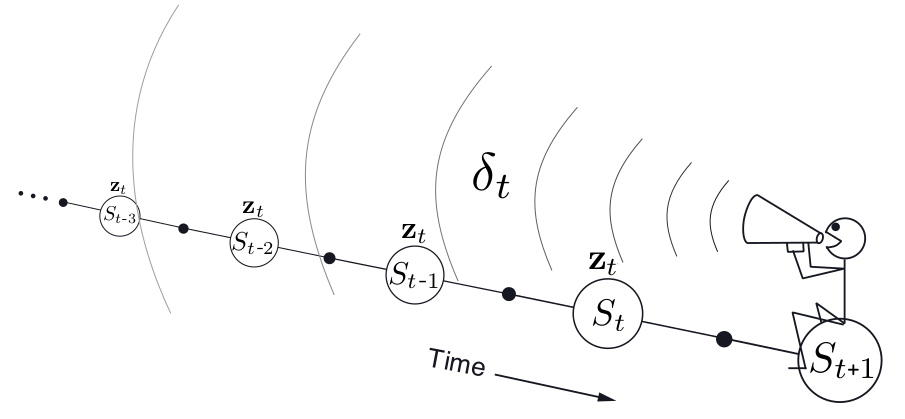
易知，当(lambda = 0)　(TD(lambda))退化成为one step semi-gradient也就是TD(0)；当(　＝　１lambda　＝　１)时，TD(1)则表现出MC的特征。

n-step Truncated (lambda)-return Methods

线下的(lambda-return)算法具有很大的局限性，因为(lambda)-return要在最后才知道，在连续状态情况下，甚至永远得不到。我们知道，一般(gammalambda<1)，因此太长时间的状态价值的影响就会消失掉，那么可以想到一种近似(lambda)-return的方法称为Truncated (lambda)-return方法：

[G_{t:h}^{lambda}dot = (1-lambda)sum_{n =1}^{h-t-1} lambda^{n-1}G_{t:t+n} + lambda^{h-t-1}G_{t:h},qquad 0 le t<hle T ]

同理可以推广出truncated TD((lambda))(TTD((lambda)))：

[w_{t+n}dot = W_{t+n-1} + alpha [G_{t:t+n}^lambda - hat v(S_t,w_{t+n-1})] abla hat v(S_t,w_{t+n-1}) ]

此算法可以以一种比较有效率的方式来改写，使其不依赖于n（当然，背后的理论关系还是依赖n的）：

[G_{t:t+k}^{lambda} = hat v(S_t,w_{t-1}) + sum_{i = t}^{t+k-1} (gamma lambda)^{i-t}delta_i' ]

其中(delta_t' dot = R_{t+1} + gammahat v(S_{t+1},w_t) -hat v(S_t,w_{t-1})).

Redoing Updates: The On-line (lambda)-return Algorithm

TTD((lambda))中n的选取是要有取舍的，n可以很大，这样更接近off-line (lambda)-return algorithm；或者很小这样更新参数不用等很久。这两种好处增加一些计算复杂度可以都得到。

其思想是这样的：在每一步时，都会得到新的数据，然后从头重新更新。

[w_{t+1}^h dot = w_t^h + alpha [G_{t:h}^h - hat v(S_t,w_t^h)] abla hat v(S_t,w_t^h),qquad 0le tle hle T. ]

(w_t dot = w_t^t)此即为on-line (lambda)-return algorithm.

True On-line TD((lambda))

借助eligibility trace，将on-line (lambda) -return 的前向视角转变成后向视角即成为true on-line TD((lambda)).

[w_{t+1}dot = w_t + alpha delta_t z_t + alpha(w_t^Tx_t - w_{t-1}^Tx_t)(z_t - x_t) ]

其中$hat v(s,w) = w^T x(s), x_tdot = x(S_t), delta_t dot = R_{t+1} +gammahat v(S_{t+1},w_t)- hat v(S_t,w_t), z_t = dot = gammalambda z_{t-1}+(1-alpha gammalambda z_{t-1}^Tx_t)x_t $.

# True On-line TD(lambda) for estimating w^T x = v_pi
Input: the policy pi to be evaluated
Input: a feature function x: S_plus --> R such that x(terminal,.) = 0
Algorithm parameters: step size alpha > 0, trace decay rate lambda in [0,1]
Initialize value-function weights w in R

Loop for each episode:
    Initialize state and obtain initial feature vector x
    z = 0
    V_old = 0
    Loop for each step of episode:
        choose A from pi.
        take action A, observe R, x'(feature vector of the next state)
        V = w^T x
        V' = w^T x'
        delta = R + gamma V' - V
        z = gamma lambda z + (1- alpha gamma z^T x)x
        w = w + alpha(delta + V- V_old)z - alpha (V-V_old) x
        V_old = V'
        x = x'
    until x' = 0(signaling arrival at a terminal state)

这里的eligibility trace 称为 dutch trace, 还有一种称为replacing trace:

[z_{i,t} dot =left{egin{array}\ 1qquad ifquad x_{i,t} = 1,\ gammalambda z_{i,t-1} qquad otherwise.end{array} ight. ]

Dutch Traces in Monte Carlo Learning

Eligibility traces也可应用于Monte Carlo 相产算法之中。

在梯度Monte Carlo算法的线性版本中：

[w_{t+1} dot = w_t +alpha [G - w_t^Tx_t]x_t,qquad 0 le t le T. ]

其中Ｇ是在episode结束后得到的奖励，因此没有下标，也没有折扣因子。因为MC方法只能在episode结束后更新参数，这个特点我们不试图改进，而是在尽力将计算分布在各个时间步上。

[egin{array}\ w_T& =& w_{T-1} + alpha(G - w_{T-1}^Tx_{T-1})x_{T-1}\ &=& w_{T-1} +alpha x_{T-1}(-x_{T-1}^Tw_{T-1})+alpha Gx_{T-1}\ &=& (I - alpha x_{T-1}x_{T-1}^T)w_{T-1}+alpha Gx_{T-1}\ &=& F_{T-1}w_{T-1}+alpha Gx_{T-1} end{array} ]

其中(F_t dot = I - alpha x_t x_t^T)是一个遗忘矩阵或称衰退矩阵（forgetting or fading matrix), 可以递归得到。

Ｓarsa((lambda))

Sarsa((lambda))是一个TD方法，与TD((lambda))类似，只不过，Sarsa((lambda))是针对state-action pair的：

[w_{t+1}dot = w_t +alpha delta_t z_t ]

其中：

[delta dot = R_{t+1}+gamma hat q(S_{t+1},A_{t+1},w_t) - hat q(S_t,A_t,w_t) ]

而：

[egin{array}\ z_{-1} &=& 0,\ z_t&=& gamma lambda z_{t-1}+ ablahat q(S_t,A_t,w_t),qquad 0le tle T. end{array} ]

# Sarsa(lambda) with binary features and linear function approximation for estimating # w^T x q_{pi} or q*
Input: a function F(s,a) returning teh set of (indices of ) active features for s,a
Input: a policy pi (if estimating q_pi)
Algorithm parameteres: step size alpha > 0, trace decay rate lambda in [0,1]
Initialize: w= (w1,...,wd)^T in R^d z = (z1,...,z_d)^T in R^d

Loop for each episode:
    Initialize S
    Choose A from pi(.|S) or e-greedy according to q_hat(S,.,w)
    z = 0
    Loop for each step of episode:
       take action A, observe R,S'
       delta =  R
       Loop for i in F(S,A):
           delta = delta - w_i
           z_i = z_i + 1  (accumulating traces)
           or z_i = 1 (replacing traces)
       If S' is terminal then:
            w = w + alpha delta z
            Go to next episode
       Choose A' in pi(.|S) or near greedily q_hat(S',.,w)
       Loop for i in F(S',A'): dleta = delta + gamma w_i
       w = w + alpha delta z
       z = gamma lambda z
       S = S', A = A'

# True Online Sarsa(lambda) for estimating w^Tx = q_pi or q*
Input: a feature function x: s_plus x A = R^d such that x(terminal,.) = 0
Input: a policy pi (if estimating q_pi)
Algorithm parameters: step size alpha >0, trace decay rate lambda in [0,1]
Initialize: w in R^d

Loop for each episode:
    Initialize S
    Choose A from pi(.|S) or nearly greedily from S using w
    x = x(S,A)
    z = 0
    Q_old = 0
    Loop for each step of episode:
        Take action A, observe R,S'
        Choose A' from pi(.|S') or near greedily from S' using w
        x' = x(S',A')
        Q = w^Tx
        Q' = w^Tx'
        delta = R + gamma Q' - Q
        z = gamma lambda z + (1 - alpha gamma lambda z^T x) x
        w = w + alpha(delta + Q - Q_old )z - alpha(Q - Q_old) x
        Q_old = Q'
        x = x'
        A = A'
    until S' is terminal