机器学习五 EM 算法

引言
- 经典示例
EM算法
GMM 推导
参考文献:

引言

Expectation maximization (EM) 算法是一种非常神奇而强大的算法. EM算法于 1977年由Dempster 等总结提出. 说EM算法神奇而强大是因为它可以解决含有隐变量的概率模型问题.

EM算法是一个简单而又复杂的算法. 说它简单是因为其操作过程就两步, E(expectation)步: 求期望; M(maximization)步, 求极大. 说它复杂,是因为刚刚学习的时候,你会发现EM算法并不像之前的算法那么的直观, 而且推导过程的tricks 理解起来也颇费精力. 不过,所谓'来者如临高山,往者如观逝水.' You can do IT!

经典示例

EM算法有一些非常经典的例子, 比如'硬币问题','小球问题','男女同学身高问题'等等. 比如硬币问题: 有A, B, C三枚硬币, 这些硬币掷出正面的概率分别为 (pi), p, q. 先掷A硬币, 根据其结果选择掷B, 还是C. 然后投掷所选硬币, 投掷结果,正面记 1, 反面记 0. 独立地重复 n 次试验,比如最终结果是 1,0,1,1,0,1,0,0,1,0,0,1,0,1,1,0,0,1,1,1 (也即 n = 20). 那么问 (pi), p, q分别是多少?

'小球问题'类似, 咱们介绍下'男女身高问题': 某大学进行体检, 每位同学的身高都记录下来:1.72, 1.58, 1.67, 1.89, …, 然后只根据身高数据(也即不知道某一身高数据(如 1.67)是来男同学还是女同学) 推测出这个学校学生的男女比例, 及男, 女同学各自的概率分布(假设均服从高斯分布).

怎么样, 有思路吗? 是不是这些看似简单的问题而又接近生活的问题, 其实并不太好解决?

我和一样, 在没有邂逅EM算法时, 也只能望洋兴叹.

EM算法

设样本数据: ({x_1, x_2, dots,x_n}) ,相互独立; 样的隐变量为 Z: ({z_1,z_2,dots,z_m}), 现在求出样本空间每个数据的隐变量, 及每个隐变量(也可能是连续的)相关的分布参数( heta).

这个需要解释下, 也就是说,对于一组观测数据, 其背的隐变量是怎样的情况(比如有一个数据1.72, 这个身高是男同学的还是女同学的(男,女就是陷变量)? 其概率分别是多少? 二者的比比例呢?)

在没有隐变量, 变隐变量已知的情况下, 求概率分布(( heta)) 最常用, 最方便的方法就是最大似然估计(maximization likelihood estimation, MLE):

[L( heta) = Pi_{i = 1}^n p(x_i, heta) ]

或者对数形式:

[l( heta) = sum_{i=1}^nlog p(x_i, heta) ]

但当隐变量存在且未知时, 那这个问题就复杂了:

[l(z, heta) = sum_{i=1}^nlog p(x_i,z, heta) ]

因为隐变量 z 未知, 所以求解参数( heta) 就变得困难了, 就算要求 z 参数 ( heta) 未知, 也不太好求解.

EM 算法就是为解决此问题而生的. EM 算法最终应用的也是MLE, 而MLE不能正常实施的根本原因就是隐变量未知, 如果隐变量已知了, 问题就解决了. 那如何让隐变量'已知'呢? 加'先验'啊. 我根据先验知识给出情况隐变量的,那参数 ( heta) 就可以求出来了. 当然这样的先验误差会很大的. 当我们求出参数后, 参数就算已知了, 反过来就可以推导出更'准确'的隐变量了. 这样如此往复, 隐变量, 参数相互作用, 最终就可得出的结果了.

既然是MLE, 那还是要:

[max_{z , heta} l(z, heta) ]

其中

[egin{array} \ l(z, heta)& = & sum_{i=1}^nlog p(x_i,z, heta)\ &=& sum_{i=1}^n log sum_{j = 1}^m p(x_i,z_j, heta)\ &=& sum_{i =1}^n logsum_{j = 1}^m Q_i(z_j)frac{p(x_i,z_j, heta)}{Q_i(z_j)}\ end{array} ]

上式第一步应用的是全概率公式, 第二步 (Q(z)) 是 z 的某种分布, 说是'某种' 是因为为了给出隐变量的先验, 至少需要把隐变量的分布表示出来(或剥离出来). 既然是某种分布, 则:

[sum_{j = 1}^m Q_i(z_j) =1 ]

接下来用到的一个知识是Jensen不等式(Jensen Inequality):

对于凸函数 f 有:

[E[f(X)] ge f(EX) ]

其中X 是随机变量. 下面这张图很好的展示了此等关系.

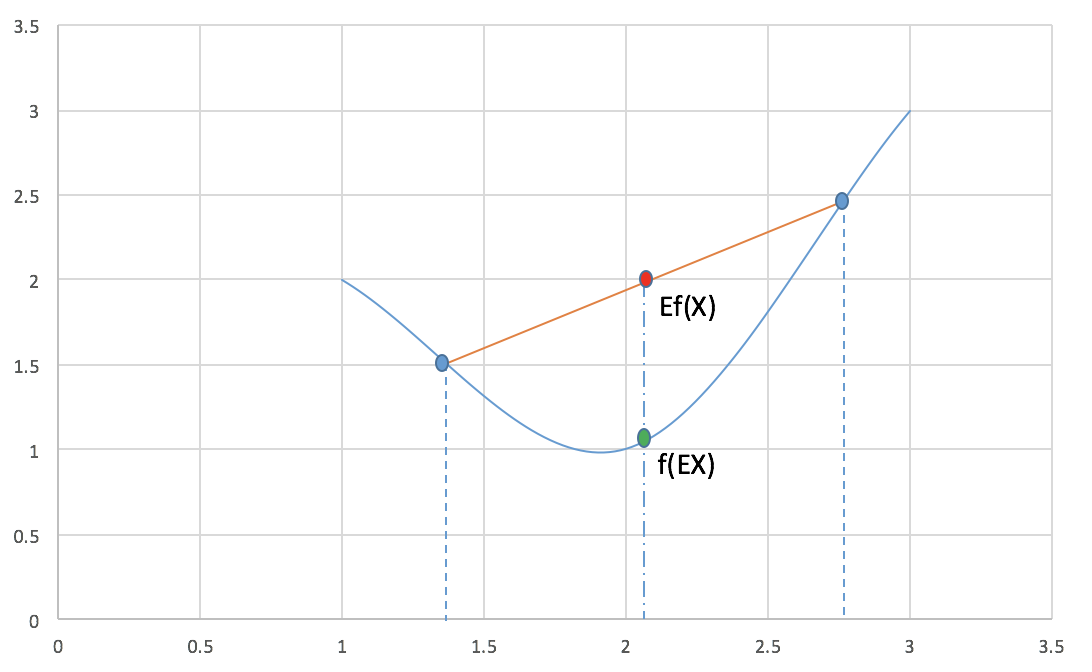
现在再看下(5)式, 你会发现:

[egin{array}\ l(z, heta) &=& sum_{i =1}^n logsum_{j = 1}^m Q_i(z_j)frac{p(x_i,z_i, heta)}{Q_i(z_j)}\ & ge & sum_{i =1}^nsum_{j = 1}^m Q_i(z_j) logfrac{p(x_i,z_j, heta)}{Q_i(z_j)}\ end{array} ]

上式可以看作是对(l(z, heta)) 求下界, 而这个下界一定程度上取决于(Q(z_j)), (frac{p(x_i,z_i, heta)}{Q(z_j)}), 也就是说, 我们可以调整此二者使这个下界尽可能的大, 也就尽可能的接近(l(z, heta)), 这个下界最大才可能等于(l(z, heta)), 这也是取等号的条件. 换句话说, 什么情况下取等号? 根据 Jensen 不等式, 只有当(frac{p(x_i,z_i, heta)}{Q(z_j)})为定值时才可以(为定值,以上图为例,也就是(x_1, x_2) (图上两蓝色点)相等, 也就是非常非常''接近'',最终成为同一个点了.). 也就是说, 无论如何无论如何调整z 隐变量, 这个值都不会变化了(都是同一个某点), 不妨设为 c:

[frac{p(x_i,z_j, heta)}{Q_i(z_j)} = c ]

由(6),(9)式,消去 c 可得:

[Q_i(z_j)=frac{p(x_i,z_j, heta)}{sum_{j= 1}^m p(x_i,z_j, heta)} = frac{p(x_i,z_j, heta)}{p(x_i, heta)} = p(z_j|x_i) ]

终于知道了, 所谓的隐变量的'某'种分布就是已知数据观测值时隐变量的条件概率.

这样 EM算法就基本'搞定'隐变量了, 那么EM算法(变了形的MLE)的基本步骤:

E步:

[Q_i(z_j)=frac{p(x_i,z_j, heta)}{sum_{j= 1}^m p(x_i,z_j, heta)} = p(z_j|x_i),\ i = 1,2,dots,n,quad j = 1,2,dots,m ]
M步: 求MLE:

[max_ heta l= sum_{i =1}^nsum_{j = 1}^m Q_i(z_j) logfrac{p(x_i,z_j, heta)}{Q_i(z_j)} ]

GMM 推导

对于学生身高问题, 是经典的高斯混合模型(Gaussian Mixed Model, GMM). 设随机变量 X 是由 k 个高斯分布混合而成, 各个高斯分布的概率分别为(psi_1,psi_2,dots,psi_k), 且第 i 个分布的均值方差为 ((mu_i, sigma_i)). 现在的要求是已知一系列样本(x_1, x_2, dots,x_n), 试估计 (psi, u,sigma).

仍然, 我们的方式还是最大化下式:

[l( heta) = sum_{i = 1}^nlog p(x_i,z, heta) =sum_{i=1}^n log sum_{j = 1}^k p(x_i,z_j, heta) ]

这里的隐变量即是分布类似别了(即哪个高斯分布, j 取 (1,…,k)的哪个).

因为推出公式了, 直接代入就可以了:

第一步(E步):

[Q_i(z_j) = p(z_j|x_i, heta) = p(z_j|x_i,psi, u,sigma)=frac{p(x_i,z_j, heta)}{sum_{j= 1}^m p(x_i,z_j, heta)} ]

第二步(M步):

[max l( heta) = max sum_{i=1}^n sum_{j = 1}^k Q_i(z_j)logfrac{p(x_i,z_j, heta)}{Q_i(z_j)} ]

因为是高斯分布,所以p的形式:

[p(x_i,z_j, heta) = p(x_i,z_j,mu_j,sigma_j) = frac{1}{sqrt{2pi sigma_j}}exp(-frac{1}{2sigma_j^2}(x_i - mu_j)^2) cdot psi_j ]

代入(15)式:

[egin{array}\ max l(mu,sigma) &=& max_{ heta} sum_{i=1}^n sum_{j = 1}^k Q_i(z_j)logfrac{frac{1}{sqrt{2pi sigma_j}}exp(-frac{1}{2sigma_j^2}(x_i - mu_j)^2) cdot psi_j}{Q_i(z_j)}\ &=& max_{ heta} sum_{i=1}^n sum_{j = 1}^k Q_i(z_j)((-frac{1}{2}log(2pisigma_j) \ &&qquad-frac{1}{2sigma_j^2}(x_i - mu_j)^2 + logpsi_j- log(Q_i(z_j))\ end{array} ]

对上式中的(mu,sigma) 分别求导即可得出结果:

[egin{array}\ frac{partial l(mu_j)}{partial mu_j} &=& sum_{i=1}^n Q_i(z_j)cdot(-frac{(x-mu_j)}{sigma_j}) = 0\ &==>& mu_j = frac{sum_{i=1}^n Q_i(z_j)x_i}{sum_{i =1}^nQ_i(z_j)} end{array} ]

同理:

[sigma_j = frac{sum_{i =1}^nQ_i(z_j) (x_j - mu_j)^2}{sum_{j = 1}^mQ_i(z_j)} ]

对于 (psi) 的求解稍微麻烦些, 不过也很自然, 因$psi $ 有如下约束:

[sum_{j = 1}^k psi_k = 1 ]

因此要与(17)式构建Lagrange 方程:

[mathscr{L(psi)} = l(psi)+ lambda(sum_{j=1}^kpsi_j - 1) ]

对(psi_j) 求导即可得到:

[psi_j = frac{1}{n}sum_{i=1}^nQ_i(z_j) ]

对于硬币问题, 只需把上面的高斯分布换成Bernoulli 分布即可.

参考文献:

统计学习方法, 李航, 2012, 清华大学出版社;
Pattern Recognition and Machine learning, Christopher M. Bishop, 2006, Springer;
The EM algorithm, JerryLead, 2011, cnblogs;