趣谈整数拆分(下)- 从“拉马努金”到“计算机算法”
上期我介绍了最初数学家对整数拆分的研究——从 “ 欧拉 ” 到 “ 拉马努金 ”,当然这个故事没有结束,计算机的出现也为此开辟了新的道路。下面的文章可以提前阅读一下:
无忧公主
1 拉马努金
上次有讲到过介绍拉马努金的电影《 The man who knew Infinity (知无涯者)》,我抽空欣赏过了,其中有讲到他对整数拆分数的研究。当时在英国剑桥大学的三一学院中,一位组合数学教授不相信一个来自印度的、没有接受过教育的人,能够发现自己始终认为不存在的公式。他们分别花了一个晚上,一人手算,一人用公式计算。在对照计算结果——p (200) 时,教授简直被震撼了:误差不超过2%!


上图是电影中的截图,上面蓝笔写的数据是正确的
教授手工计算的过程是极为繁琐和易错的,所以接下来,我想介绍一个更为高效、一定正确的做法。
2 多项式乘法
欧拉的做法是多项式乘法,虽然人工拆括号会很麻烦,但写程序处理就会方便一些了。下面是实现的代码:

这个算法的复杂度是 O(n^3) 的,不过由于计算 p(400) 以上的整数拆分数时,可能会超过 64 位整数存储范围,我开的数组大小只有 400。在普通计算机上,这个时间和空间复杂度都是可以接受的。
3 三维递归
另一种比较容易想到的方法是三维递归,设 f ( n , m , k ) 表示将 n 拆分为 m 个不超过 k 的整数的方案个数。这里加上 k 的限制,是为了保证每次划分出的数,是由大到小排序的,可以避免重复。于是我们可以得到:
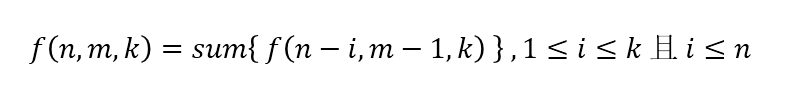
列出这个状态转移方程以后,就可以用递归 + 记忆化搜索(记录下已访问过的结果,加快速度)来实现了:
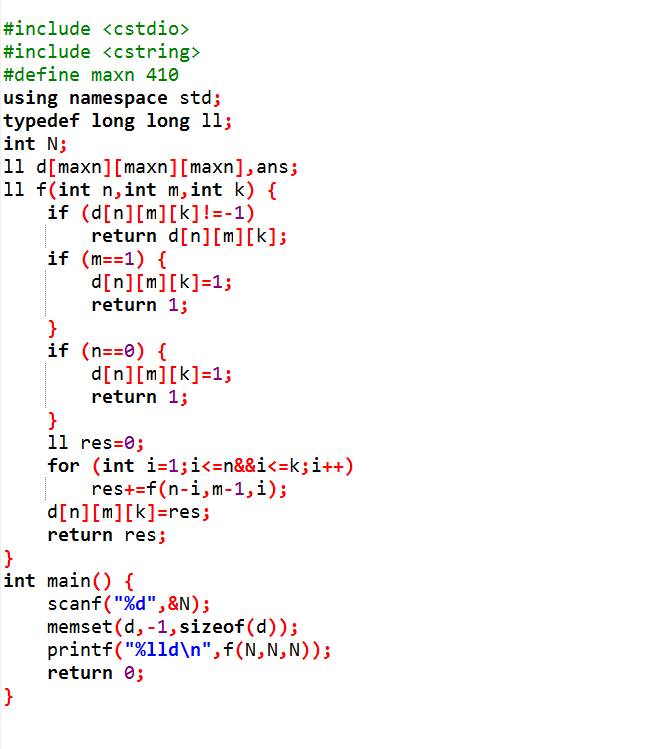
因为是三维的,复杂度与上一种方法都是 O(n^3)。
4 二维递推
把上面的递归方程稍微加工一下,可以变为二维的。设 f ( n , k ) 为将 n 拆分成不超过 k 的整数之和的方案数,那么可以列出:
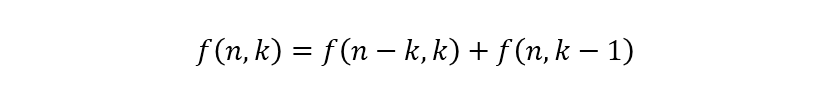
这里解释一下方程的含义,f ( n , k ) 包含 2 种情况。当拆分后有 k,则表示 f ( n-k , k ),n-k 的拆分中是否会有 k,不需要处理。若不会拆分出 k,即最大数只可能为 k-1,则表示着 f ( n , k-1 );当然,n 的拆分中是否还有 k-1,交给下一级处理了。
上期中,我的程序正是用这样的方法,计算出 p(400) 的。这种做法的确比三维递归要快,复杂度为 O(n^2)。在计算 p(400) 时,O(n^2) 和 O(n^3) 差异不是特别大,但如果到 p(4000),O(n^3) 就超时啦。

5 尾声
其实整数拆分数的研究一直没有停止,我的这 2 篇小文章也只是一个初步的介绍。大家可以到 OEIS 上了解更多关于这方面的信息(整数拆分数的编号为 A000041)。返回搜狐,查看更多