查找算法评价指标 平均查找长度 查找成功或不成功的 ASL = Σ 概率*比较次数 等概率时与数组是否有序无关,不等概率与序列有关。
顺序查找:ASL=(n+1)/2
折半查找:构建一颗判定树,每个数的层数就是查找到需要的比较次数。比较n次可以找到2^(n-1)个数字。
树表:二叉排序树,充分必要条件是中序遍历是递增的。
散列表:Hash
1.二叉排序树
假设被删结点是*p,其双亲是*f,不失一般性,设*p是*f的左孩子,下面分三种情况讨论:
(1) 若结点*p是0度,则只需修改其父结点*f的指针即可
(2) 若结点*p是1度,则只要使PL或PR 成为其父结点的左子树
(3) 若结点*p是2度,先找到*p的中序后继结点*s(*p的右子树中的最左下的结点),以*s代替*p,执行(2)将*s的左子树链到*s的父结点*q的左(或右)链上。
#include <iostream> #include <cstdio> using namespace std; typedef struct Node { int data; int flag; Node *lchild, *rchild; } *BTree; BTree Insert(BTree &T, int key) { BTree pre = T, p = T; while (p) { if (p->data == key) return T; pre = p; p = (key < p->data) ? p->lchild : p->rchild; } p = new Node; p->data = key; p->lchild = p->rchild = NULL; if (T == NULL) T = p; else if (key < pre->data) pre->lchild = p; else pre->rchild = p; return T; } void Del(BTree &T, int key) { BTree p = T, pre, s; while (p) { if (p->data == key) break; pre = p; p = (key < p->data) ? p->lchild : p->rchild; } if (!p) return; if (p->lchild == NULL && p->rchild == NULL) { if (p == T) T = NULL; //删除的是根节点 else if (p == pre->lchild) pre->lchild = NULL; else pre->rchild = NULL; free(p); } else if (p->lchild == NULL && p->rchild != NULL) { if (pre->lchild == p) pre->lchild = p->rchild; else pre->rchild = p->rchild; free(p); } else if (p->rchild == NULL && p->lchild != NULL) { if (pre->lchild == p) pre->lchild = p->lchild; else pre->rchild = p->lchild; free(p); } else if (p->lchild != NULL && p->rchild != NULL) { pre = p; s = p->rchild; while (s->lchild) { //中序前驱 pre = s; s = s->lchild; } p->data = s->data; //以p的中序前趋结点s代替p(即把s的数据复制到p中) if (pre != p) pre->lchild = s->rchild; //重接q的右子树 else p->rchild = s->rchild; //重接q的左子树。 free(s); } } void Debug(BTree &T) { if (T) { Debug(T->lchild); printf("%d ", T->data); Debug(T->rchild); } } int main() { BTree T; for (int i = 0; i < 10; i++) Insert(T, rand() % 100); Debug(T); puts(""); Del(T, 67); Debug(T); return 0; }
2.平衡二叉树(AVL树)
定义:平衡二叉树或为空树,或为如下性质的二叉排序树:
(1)左右子树深度之差的绝对值不超过1;
(2)左右子树仍然为平衡二叉树.
平衡因子BF=左子树深度-右子树深度.
平衡二叉树每个结点的平衡因子只能是1,0,-1。若其绝对值超过1,则该二叉排序树就是不平衡的。
结构体定义如下
#define LH 1 //左高 #define EH 0 //等高 #define RH -1 //右高 typedef struct Node { int data; int bf; //结点的平衡因子 Node *LChild, *RChild; //左、右孩子指针 }*AVL;
一、如何保持平衡
若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。首先要找出插入新结点后失去平衡的最小子树根结点的指针。然后再调整这个子树中有关结点之间的链接关系,使之成为新的平衡子树。当失去平衡的最小子树被调整为平衡子树后,原有其他所有不平衡子树无需调整,整个二叉排序树就又成为一棵平衡二叉树。
失去平衡的最小子树是指以离插入结点最近,且平衡因子绝对值大于1的结点作为根的子树。假设用A表示失去平衡的最小子树的根结点,则调整该子树的操作可归纳为下列四种情况。
(1)L型旋转
由于在A的左孩子B的左子树上插入结点F,使A的平衡因子由1增至2而失去平衡。故需进行一次顺时针旋转操作。 即将A的左孩子B向右上旋转代替A作为根结点,A向右下旋转成为B的右子树的根结点。而原来B的右子树则变成A的左子树。
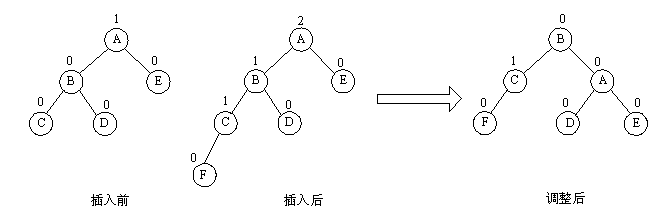
void L_Rotate(AVL &p) { Node *rc = p->RChild; p->RChild = rc->LChild; rc->LChild = p; p->bf = rc->bf = EH; p = rc; }
(2)R型旋转
由于在A的右孩子C 的右子树上插入结点F,使A的平衡因子由-1减至-2而失去平衡。故需进行一次逆时针旋转操作。即将A的右孩子C向左上旋转代替A作为根结点,A向左下旋转成为C的左子树的根结点。而原来C的左子树则变成A的右子树。
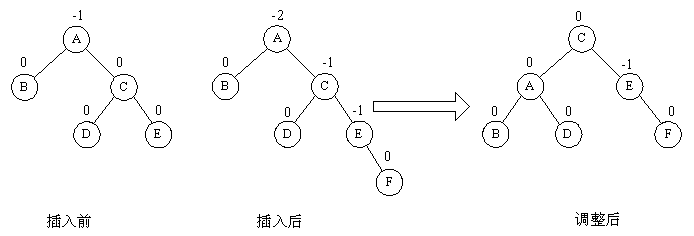
void R_Rotate(AVL &p) { Node *lc = p->LChild; p->LChild = lc->RChild; lc->RChild = p; p->bf = lc->bf = EH; p = lc; }
(3)LL与LR型平衡旋转
由于在A的左孩子B的右子数上插入结点F,使A的平衡因子由1增至2而失去平衡。故需进行两次旋转操作(先逆时针,后顺时针)。即先将A结点的左孩子B的右子树的根结点D向左上旋转提升到B结点的位置,然后再把该D结点向右上旋转提升到A结点的位置。即先使之成为LL型,再按LL型处理。
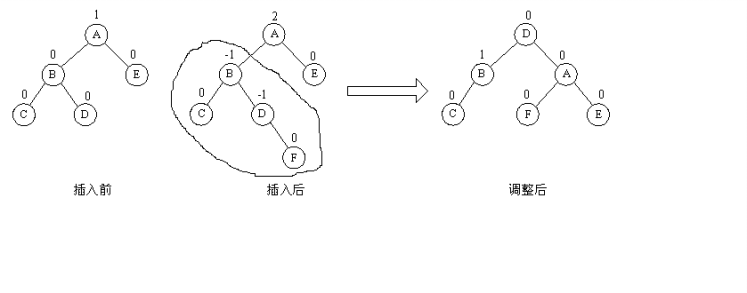
如图中所示,即先将圆圈部分先调整为平衡树,然后将其以根结点接到A的左子树上,此时成为LL型,再按LL型处理成平衡型。
void LeftBalance(AVL &T) { //对以指针T所指结点为根的二叉树作左平衡旋转处理,指针T指向新的根结点 AVL lc, rd; lc = T->LChild; switch (lc->bf) { //判断*T的左子树的平衡因子 case LH: //LL,只需要一次R旋转 T->bf = lc->bf = EH; R_Rotate(T); break; case RH: //LR,新结点插入在*T的左孩子的右子树上,需要对左子树L旋转,和对T作R旋转 rd = lc->RChild; //rd指向*T的左孩子的右子树的根 switch (rd->bf) { //修改*T及其左孩子的平衡因子 case LH: T->bf = RH; lc->bf = EH; break; case EH: T->bf = lc->bf = EH; break; case RH: T->bf = EH; lc->bf = LH; break; } L_Rotate(T->LChild); //对*T的左子树作左旋平衡处理 R_Rotate(T); //对*T作右旋平衡处理 rd->bf = EH; //是新的根节点,保证平衡 } }
(4)RR与RL型平衡旋转
由于在A的右孩子C的左子树上插入结点F,使A的平衡因子由-1减至-2而失去平衡。故需进行两次旋转操作(先顺时针,后逆时针),即先将A结点的右孩子C的左子树的根结点D向右上旋转提升到C结点的位置,然后再把该D结点向左上旋转提升到A结点的位置。即先使之成为RR型,再按RR型处理。
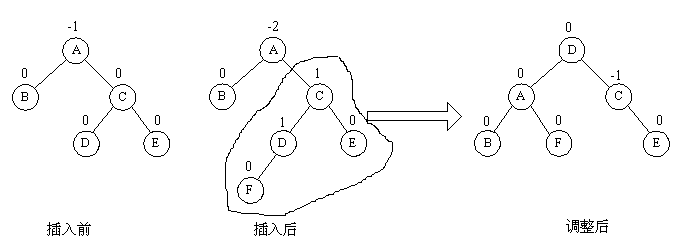
如图中所示,即先将圆圈部分先调整为平衡树,然后将其以根结点接到A的左子树上,此时成为RR型,再按RR型处理成平衡型。
void RightBalance(AVL &T) { AVL ld, rc; rc = T->RChild; switch (rc->bf) { case RH: //RR,只需要一次L旋转 T->bf = rc->bf = EH; L_Rotate(T); break; case LH: //RL,需要对右子树R旋转,和对T作L旋转 ld = rc->LChild; switch (ld->bf) { case LH: T->bf = EH; rc->bf = LH; break; case EH: T->bf = rc->bf = EH; break; case RH: T->bf = RH; rc->bf = EH; break; } ld->bf = EH; R_Rotate(T->RChild); L_Rotate(T); break; } }
二、如何判断插入后对哪个点平衡操作
采用taller判断是否需要继续进行平衡操作。如果平衡了就设taller为0,如果插入点taller = 1,或向上更新时出现了潜在的不平衡情况taller = 1。平衡操作后要置taller = 0。
bool Insert(AVL &T, int key, bool &taller) { //若在平衡的二叉树T中不存在和e有相同关键字的结点,则插入一个数据元素 //为e的新结点,并返回1,否则返回0,旋转处理,布尔变量taller反映是否需要继续向上检验平衡因子 if (!T) { //插入新结点,树“长高”,置taller为true T = (AVL) malloc(sizeof(Node)); T->data = key; T->LChild = T->RChild = NULL; T->bf = EH; taller = 1; return 1; } if (key == T->data) { //树中已存在和e有相同关键字的结点 taller = 0; return 0; } if (key < T->data) { //在T的左子树中搜索 if (!Insert(T->LChild, key, taller)) //未插入返回 return 0; if (taller) //已插入到T的左子树中且左子树“长高” switch (T->bf) { //检查T的平衡度 case LH: //原本左子树比右子树高,需要作左平衡处理 LeftBalance(T); taller = 0; break; case EH: //原本左、右子树等高,需要作左平衡处理 T->bf = LH; taller = 1; break; case RH: //原本右子树比左子树高 T->bf = EH; taller = 0; break; } } else { //在T的右子树中搜索 if (!Insert(T->RChild, key, taller)) //未插入 return 0; if (taller) //已插入到T右子树且右子树长高 switch (T->bf) { //检查T的平衡度 case LH: T->bf = EH; taller = 0; break; case EH: T->bf = RH; taller = 1; break; case RH: RightBalance(T); taller = 0; break; } } return 1; }
三、在AVL树中删除元素
bool Delete(AVL &T, int key, bool &shorter) { if (!T) { shorter = 0; return 0; } if (key == T->data) { //找到了需要删除的结点 //如果该结点的lchild rchild 至少有一个为NULL 则大功告成 AVL q = T; if (!T->LChild) { T = T->RChild; free(q); shorter = 1; return 1; } else if (!T->RChild) { T = T->LChild; free(q); shorter = 1; return 1; } else { AVL s = T->LChild; while (s->RChild) s = s->RChild; T->data = s->data; key = s->data; } } if (key <= T->data) { if (!Delete(T->LChild, key, shorter)) return 0; if (shorter) { switch (T->bf) { case LH: //T平衡因子EH,深度减少,需向上更新shorter = 1 T->bf = EH; shorter = 1; break; case EH: T->bf = RH; shorter = 0; break; case RH: RightBalance(T); if (T->RChild->bf == EH) shorter = 0; else shorter = 1; break; } } } else { if (!Delete(T->RChild, key, shorter)) return 0; if (shorter) { switch (T->bf) { case LH: LeftBalance(T); if (T->LChild->bf == EH) shorter = 0; else shorter = 1; break; case EH: T->bf = LH; shorter = 0; break; case RH: T->bf = EH; shorter = 1; break; } } } return 1; }
四、作为排序树,中序遍历AVL树就得到排序
void output(AVL T) { if (T) { output(T->LChild); printf("%d ", T->data); output(T->RChild); } } int main() { vector<int> map; map.clear(); bool flag; int key; AVL Root = NULL; for (int i = 0; i < 10; i++) { key = rand() % 1000; map.push_back(key); Insert(Root, key, flag); } output(Root); puts(""); for (int i = 0; i < 8; i++) { Delete(Root, map[i], flag); output(Root); puts(""); } return 0; }
3.红黑树
红黑树,一种二叉查找树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。
通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
红黑树的5个性质:
1)每个结点要么是红的,要么是黑的。
2)根结点是黑的。
3)每个叶结点,即空结点(NIL)是黑的。
4)如果一个结点是红的,那么它的俩个儿子都是黑的。
5)对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
一,插入
在对红黑树进行插入操作时,我们一般总是插入红色的结点,因为插入一个红色结点只会破坏性质2或性质4。
那么,我们插入一个结点后,可能会使原树的哪些性质改变列?
由于,我们是按照二叉树的方式进行插入,因此元素的搜索性质不会改变。
如果插入的结点是根结点,性质2会被破坏,如果插入结点的父结点是红色,则会破坏性质4。
我们的回复策略很简单,
其一、把出现违背红黑树性质的结点向上移,如果能移到根结点,那么很容易就能通过直接修改根结点来恢复红黑树的性质。直接通过修改根结点来恢复红黑树应满足的性质。
其二、穷举所有的可能性,之后把能归于同一类方法处理的归为同一类,不能直接处理的化归到下面的几种情况,
情况1:插入的是根结点
原树是空树,此情况只会违反性质2。
对策:直接把此结点涂为黑色。
情况2:插入的结点的父结点是黑色
此不会违反性质2和性质4,红黑树没有被破坏。
对策:什么也不做。
情况3:当前结点的父结点是红色且祖父结点的另一个子结点(叔叔结点)是红色
与此同时,又分为父结点是祖父结点的左子还是右子,对于对称性,我们只要解开一个方向就可以了。我们先考虑父结点为祖父左子的情况。
父节点为红色性质4被破坏。
对策:将当前节点的父节点和叔叔节点涂黑,祖父结点涂红,把当前结点指向祖父节点,从新的当前节点重新开始算法。
如插入节点4: 变为:

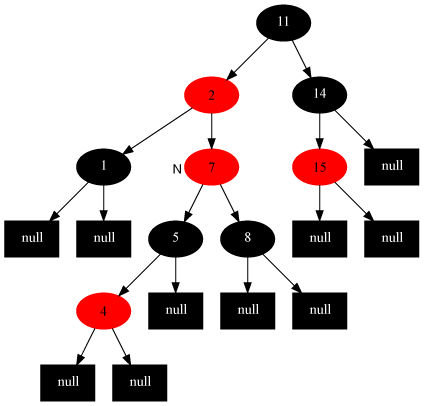
情况4:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的右子
父节点为红色性质4被破坏。
对策:当前节点的父节点做为新的当前节点,以新当前节点为支点左旋。
如插入节点7: 变为:

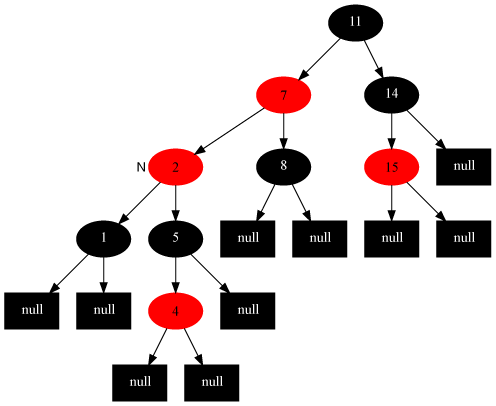
情况5:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的左子
解法:父节点变为黑色,祖父节点变为红色,在祖父节点为支点右旋
如插入节点7: 变为:

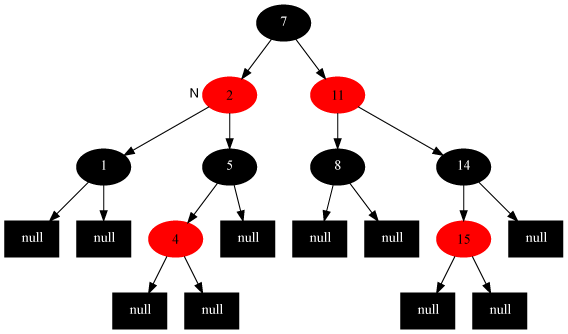
#include <iostream> #include <cstring> #include <iostream> #include <vector> using namespace std; #define RED 0 #define BLACK 1 struct RB_Node { bool COLOR; RB_Node* right; RB_Node* left; RB_Node* parent; int key; RB_Node() { right = NULL; left = NULL; parent = NULL; } }; RB_Node *m_nullNode; RB_Node *m_root; void init() { m_nullNode = new RB_Node(); m_root = m_nullNode; m_nullNode->right = m_root; m_nullNode->left = m_root; m_nullNode->parent = m_root; m_nullNode->COLOR = BLACK; } bool Empty() { if (m_root == m_nullNode) return 1; return 0; } //左旋代码实现 void RotateLeft(RB_Node* node) { if (node == m_nullNode || node->right == m_nullNode) { return; //can't rotate } RB_Node* lower_right = node->right; lower_right->parent = node->parent; node->right = lower_right->left; if (lower_right->left != m_nullNode) { lower_right->left->parent = node; } if (node->parent == m_nullNode) //rotate node is root { m_root = lower_right; m_nullNode->left = m_root; m_nullNode->right = m_root; //m_nullNode->parent = m_root; } else { if (node == node->parent->left) { node->parent->left = lower_right; } else { node->parent->right = lower_right; } } node->parent = lower_right; lower_right->left = node; } //右旋代码实现 void RotateRight(RB_Node* node) { if (node == m_nullNode || node->left == m_nullNode) { return; //can't rotate } RB_Node* lower_left = node->left; node->left = lower_left->right; lower_left->parent = node->parent; if (lower_left->right != m_nullNode) { lower_left->right->parent = node; } if (node->parent == m_nullNode) //node is root { m_root = lower_left; m_nullNode->left = m_root; m_nullNode->right = m_root; } else { if (node == node->parent->right) { node->parent->right = lower_left; } else { node->parent->left = lower_left; } } node->parent = lower_left; lower_left->right = node; } inline RB_Node* InOrderPredecessor(RB_Node* node) { if (node == m_nullNode) //null node has no predecessor { return m_nullNode; } RB_Node* result = node->left; //get node's left child while (result != m_nullNode) //try to find node's left subtree's right most node { if (result->right != m_nullNode) { result = result->right; } else { break; } } //after while loop result==null or result's right child is null if (result == m_nullNode) { RB_Node* index = node->parent; result = node; while (index != m_nullNode && result == index->left) { result = index; index = index->parent; } result = index; // first right parent or null } return result; } inline RB_Node* InOrderSuccessor(RB_Node* node) { if (node == m_nullNode) //null node has no successor { return m_nullNode; } RB_Node* result = node->right; //get node's right node while (result != m_nullNode) //try to find node's right subtree's left most node { if (result->left != m_nullNode) { result = result->left; } else { break; } } //after while loop result==null or result's left child is null if (result == m_nullNode) { RB_Node* index = node->parent; result = node; while (index != m_nullNode && result == index->right) { result = index; index = index->parent; } result = index; //first parent's left or null } return result; } //查找key RB_Node* find(int key) { RB_Node* index = m_root; while (index != m_nullNode) { if (key < index->key) { index = index->left; } else if (key > index->key) { index = index->right; } else { break; } } return index; } void InsertFixUp(RB_Node*); void DeleteFixUp(RB_Node*); //因为将z着为红色,可能会违反某一红黑性质 //所以需要调用下面的RB-INSERT-FIXUP(T, z)来保持红黑性质。 bool Insert(int key) { RB_Node* insert_point = m_nullNode; RB_Node* index = m_root; while (index != m_nullNode) { insert_point = index; if (key < index->key) { index = index->left; } else if (key > index->key) { index = index->right; } else { return 0; } } RB_Node* insert_node = new RB_Node(); insert_node->key = key; insert_node->COLOR = RED; insert_node->right = m_nullNode; insert_node->left = m_nullNode; if (insert_point == m_nullNode) //如果插入的是一颗空树 { m_root = insert_node; m_root->parent = m_nullNode; m_nullNode->left = m_root; m_nullNode->right = m_root; m_nullNode->parent = m_root; } else { if (key < insert_point->key) { insert_point->left = insert_node; } else { insert_point->right = insert_node; } insert_node->parent = insert_point; } InsertFixUp(insert_node); //调用InsertFixUp修复红黑树性质。 return 1; } void InsertFixUp(RB_Node* node) { while (node->parent->COLOR == RED) { if (node->parent == node->parent->parent->left) { RB_Node* uncle = node->parent->parent->right; if (uncle->COLOR == RED) //插入情况1,z的叔叔y是红色的。 { node->parent->COLOR = BLACK; uncle->COLOR = BLACK; node->parent->parent->COLOR = RED; node = node->parent->parent; } else if (uncle->COLOR == BLACK) //插入情况2:z的叔叔y是黑色的,。 { if (node == node->parent->right) //且z是右孩子 { node = node->parent; RotateLeft(node); } else //插入情况3:z的叔叔y是黑色的,但z是左孩子。 { node->parent->COLOR = BLACK; node->parent->parent->COLOR = RED; RotateRight(node->parent->parent); } } } else //这部分是针对为插入情况1中,z的父亲现在作为祖父的右孩子 { RB_Node* uncle = node->parent->parent->left; if (uncle->COLOR == RED) { node->parent->COLOR = BLACK; uncle->COLOR = BLACK; uncle->parent->COLOR = RED; node = node->parent->parent; } else if (uncle->COLOR == BLACK) { if (node == node->parent->left) { node = node->parent; RotateRight(node); //与上述代码相比,左旋改为右旋 } else { node->parent->COLOR = BLACK; node->parent->parent->COLOR = RED; RotateLeft(node->parent->parent); //右旋改为左旋 } } } } m_root->COLOR = BLACK; } bool Delete(int key) { RB_Node* delete_point = find(key); if (delete_point == m_nullNode) { return false; } if (delete_point->left != m_nullNode && delete_point->right != m_nullNode) { RB_Node* successor = InOrderSuccessor(delete_point); delete_point->key = successor->key; delete_point = successor; } RB_Node* delete_point_child; if (delete_point->right != m_nullNode) { delete_point_child = delete_point->right; } else if (delete_point->left != m_nullNode) { delete_point_child = delete_point->left; } else { delete_point_child = m_nullNode; } delete_point_child->parent = delete_point->parent; if (delete_point->parent == m_nullNode) //delete root node { m_root = delete_point_child; m_nullNode->parent = m_root; m_nullNode->left = m_root; m_nullNode->right = m_root; } else if (delete_point == delete_point->parent->right) { delete_point->parent->right = delete_point_child; } else { delete_point->parent->left = delete_point_child; } if (delete_point->COLOR == BLACK && !(delete_point_child == m_nullNode && delete_point_child->parent == m_nullNode)) { DeleteFixUp(delete_point_child); } delete delete_point; return true; } void DeleteFixUp(RB_Node* node) { while (node != m_root && node->COLOR == BLACK) { if (node == node->parent->left) { RB_Node* brother = node->parent->right; if (brother->COLOR == RED) //情况1:x的兄弟w是红色的。 { brother->COLOR = BLACK; node->parent->COLOR = RED; RotateLeft(node->parent); } else //情况2:x的兄弟w是黑色的, { if (brother->left->COLOR == BLACK && brother->right->COLOR == BLACK) //且w的俩个孩子都是黑色的。 { brother->COLOR = RED; node = node->parent; } else if (brother->right->COLOR == BLACK) //情况3:x的兄弟w是黑色的,w的右孩子是黑色(w的左孩子是红色)。 { brother->COLOR = RED; brother->left->COLOR = BLACK; RotateRight(brother); } else if (brother->right->COLOR == RED) //情况4:x的兄弟w是黑色的,且w的右孩子时红色的。 { brother->COLOR = node->parent->COLOR; node->parent->COLOR = BLACK; brother->right->COLOR = BLACK; RotateLeft(node->parent); node = m_root; } } } else //下述情况针对上面的情况1中,node作为右孩子而阐述的。 //同样,原理一致,只是遇到左旋改为右旋,遇到右旋改为左旋,即可 { RB_Node* brother = node->parent->left; if (brother->COLOR == RED) { brother->COLOR = BLACK; node->parent->COLOR = RED; RotateRight(node->parent); } else { if (brother->left->COLOR == BLACK && brother->right->COLOR == BLACK) { brother->COLOR = RED; node = node->parent; } else if (brother->left->COLOR == BLACK) { brother->COLOR = RED; brother->right->COLOR = BLACK; RotateLeft(brother); } else if (brother->left->COLOR == RED) { brother->COLOR = node->parent->COLOR; node->parent->COLOR = BLACK; brother->left->COLOR = BLACK; RotateRight(node->parent); node = m_root; } } } } m_nullNode->parent = m_root; //最后将node置为根结点 node->COLOR = BLACK; //并改为黑色。 } void InOrderTraverse(RB_Node* node) { if (node == m_nullNode) { return; } else { InOrderTraverse(node->left); cout << node->key << " "; InOrderTraverse(node->right); } } int main() { init(); vector<int> key; for (int i = 0; i < 10; ++i) { int t = rand() % 100; key.push_back(t); Insert(t); cout << "insert:" << t << endl; //添加结点 } for (size_t i = 0; i < key.size(); i++) { cout << "Delete:" << key[i] << " : "; Delete(key[i]); InOrderTraverse(m_root); puts(""); } return 0; }
Hash表
衡量标准:hash函数,处理冲突方法,装填因子α(hash表密度)

hash函数构造方法
1.开放地址法:寻找下一个空的hash地址解决冲突
线性探测法:顺次找到下一个空地址(循环队列)发生“聚集”。
二次探测法:Hi = ( Hash(key) + di ) mod m di为增量序列12,-12,22,-22,…,q2,找到新的地址
伪随机探测法:di为伪随机数字,也是有固定顺序的。
查找时,从定位到的地址开始直到找到地址内容为空,说明不存在查找数据元素。
2.链地址法
同一hash地址的连接成一个链表,这样完全解决了聚集问题和hash表大小问题。
#define H 21997 int next[H], head[H]; void insert(int i) { int key = (p[i].x*p[i].x+p[i].y*p[i].y)%H; next[i] = head[key]; p[i].x = p[i].x; p[i].y = p[i].y; head[key] = i; } int find(int x,int y) { int key=(x*x+y*y)%H; for(int i = head[key];i != -1;i = next[i]) if(p[i].x == x && p[i].y == y) return i; return -1; }
在实现爬虫的时候,我们使用Hash结构去存储我们用过的URL的时候,有些URL可能长度很长,为了更加节省空间,我们就要对URL进行压缩,帮它减减肥,这个我们介绍这个MD5算法,可以对URL进行有效的压缩。
下面我们会讲讲MD5算法的一些细节,不过我们大可不必在意,我们只需要知道,我们对一个很长很长的字符串进行MD5压缩,返回的是一个128位整数,这个字符串就是原字符串的唯一标示符,就好像是我们的身份证一样,通过这个id就可以标识唯一的你。
MD5算法描述:MD5以512位分组来处理输入的信息,且每一分组又被划分为16个32位子分组,经过一系列的处理后,算法的输出有4个32位分组组成,将这4个32位分组级联后将生成一个128位的散列值。在MD5算法中,首先需要对信息进行填充,使其位长度对512求余的结果等于448,因此,信息的位长度将被扩展为N*512+448,在信息的后面附加一个1和无数个0,知道满足上面的条件才停止用0对信息进行填充,然后在这个结果的后面附加一个64位二进制表示的填充前的信息长度,通过这几步的处理,现在的信息字节长度=N*512+448+64=(N+1)*512,即长度恰好是512的整数倍。
在Java中,java.security.MessageDigest中定义了MD5的计算,只需要简单地调用即可得到MD5的128位整数,然后将此128位转换成十六进制表示即可。通过这样的转换就可以将很长的字符串变成长度为32的字符串。
先来看看MessageDigest这个类:
介绍:此 MessageDigest 类为应用程序提供信息摘要算法的功能,如 MD5 或 SHA 算法。信息摘要是安全的单向哈希函数,它接收任意大小的数据,并输出固定长度的哈希值。
getInstance(String algorithm):这个该类的静态方法,返回具有指定算法名称的信息摘要。
update(byte[] input):使用指定的byte数组去更新摘要,这个byte数组其实就是我们要压缩的那个字符串的数组。
digest():通过执行诸如填充之类的最终操作完成哈希计算,其实就是根据MD5算法计算出一个128位的长整数,也即使16个字节。