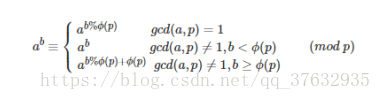2020杭电多校第一场 1005 Fibonacci Sum(二次剩余,Fibonacci通项公式)

题意

Fibonacci定义如下：

输入三个数n,c,k，计算如下表达式的值：

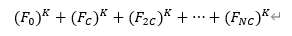
并将结果对1e9+9取模

思路:

Fibonacci的通项公式如下：

(F_i=frac{1}{sqrt{5}}*[(frac{1+sqrt{5}}{2})^i-(frac{1-sqrt{5}}{2})^i])

由于5是模1e9+9下的二次剩余，因此可以直接将该公式带入表达式中求解，其中(sqrt5)用5的二次剩余383008016代替。

令A=(frac{1+sqrt{5}}{2}),B=(frac{1-sqrt{5}}{2})，求得A=691504013，B=308495997

则((F_{ic})^k=(frac{1}{sqrt{5}})^k*(A^{ic}-B^{ic})^k)

利用二项式定理展开后，((F_{ic})^k=(frac{1}{sqrt{5}})^k* sum_{j=0}^k[(-1)^{k-j}*C_k^j*A^{icj}*B^{ic(k-j)}])

发现所有(F_i)中j相同的项可以合并，只看(A imes B)部分，合并之后是一个等比数列，初项和公比均为(A^{cj}*B^{c(k-j)})，有n项，利用等比数列求和公式可以得到其和为(x*frac{x^n-1}{x-1})，其中(x=A^{cj}*B^{c(k-j)})

就可以得到(ans=(frac{1}{sqrt{5}})^k* sum_{j=0}^k[(-1)^{k-j}*C_k^j*x*frac{x^n-1}{x-1}])

优化

直接在循环中用快速幂跑这个代码会T，需要两种优化方法：
（1）利用欧拉降幂公式

因为1e9+9是质数，因此gcd(x,p)一定为1，计算中所有需要求幂的都可以把指数对1e9+8取模

（2）在循环中需要用到x，x不需要每次用快速幂进行求，因为可以发现当前的x和前一项相比，只要乘上(A^c/B^c)就可以了，可以少算一次快速幂。

（3）取模数一定要加const，加了之后至少快了500ms，我艹

代码:

#pragma GCC optimize(2)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
const ll sqrt5=383008016;
const ll A=691504013,B=308495997;
const ll P=1e9+9;
ll fac[maxn],finv[maxn];
ll fp(ll b,ll p){
    ll ans=1;
    while(p){
        if(p&1){
            ans=ans*b%P;
        }
        p>>=1;
        b=b*b%P;
    }
    return ans;
}
void init(int n){
    fac[0]=1;
    for(int i=1;i<=n;i++){
        fac[i]=fac[i-1]*i%P;
    }
    finv[n]=fp(fac[n],P-2);
    for(int i=n-1;i>=0;i--){
        finv[i]=finv[i+1]*(i+1)%P;
    }
}
ll C(ll n,ll m){
    if(m<0 || m>n) return 0;
    return fac[n]*finv[n-m]%P*finv[m]%P;
}
ll solve(ll n,ll c,ll k){
    ll A_C=fp(A,c%(P-1));
    ll B_C=fp(B,c%(P-1));
    ll inv_B_C=fp(B_C,P-2);
    ll base=fp(B_C,k);
    ll multi=A_C*inv_B_C%P;
    ll ans=0;
    for(ll i=0;i<=k;i++){
        ll temp;
        if(base==1){
            temp=n%P;
        }
        else{
            temp=base*(fp(base,n%(P-1))-1+P)%P*fp(base-1,P-2)%P;
        }
        ll temp2=C(k,i)*temp%P;
        if((k-i)&1){
            ans-=temp2;
            ans=(ans+P)%P;
        }
        else{
            ans+=temp2;
            ans=(ans+P)%P;
        }
        base=base*multi%P;
    }
    ll inv_sqrt5=fp(sqrt5,P-2);
    ans=ans*fp(inv_sqrt5,k)%P;
    return ans;
}
int main () {
    init(100000);
    int T;
    scanf("%d",&T);
    while(T--){
        ll n,c,k;
        scanf("%lld%lld%lld",&n,&c,&k);
        ll ans=solve(n,c,k);
        printf("%lld
",ans);
    }
}