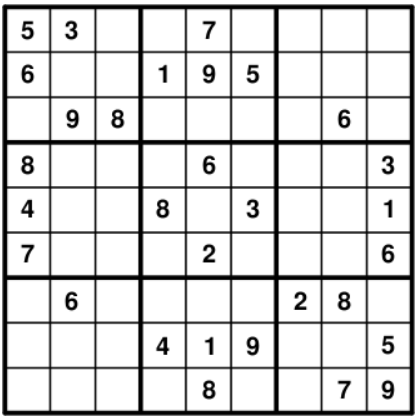
数独(Sudoku) 是一种游戏,是在9x9的表格里填上缺失的部分,以达到如下要求:
在任何一个9宫格(3x3)里,每个小格的数字都是从1到9,无缺无重。
9宫格的每一行都包含1到9的数字,无缺无重。
9宫格的每一列都包含1到9的数字,无缺无重。
如下图:
求解:
1。设定决策变量:Identify the Decision Variables
要把这个问题作为线性规划问题,不能简单定义99=81个变量。因为线性规划里没有“不等于”的条件,因而不能在宫格内/行/列使用约束条件。
但我们可以保证9宫/1行/1列数据之和等于45。从而,我们可以建议729个整形变量(0-1),意为每81个格有9个约束变量(819)。对于1个格子来说,如果其中一个数为true,则其它8个必定为false.
从而将问题简化:
2。设定目标函数 Formulate the Objective Function
数独问题没有最大或最小值,而是在寻找满足所有约束条件的变量。所以目标函数设为0也可以。
3。设定约束条件 Formulate the Constraints
下面是这729个二值决策变量需要满足的约束条件:
每一行的数字必须是1到9
每一列也是1到9
每个小格子也是1到9
每一个格子只能取一个值而且必须取一个值
已经有值的格子数值固定,不能改变
编程:
from pulp import *
# A list of strings from "1" to "9" is created
Sequence = ["1", "2", "3", "4", "5", "6", "7", "8", "9"]
# The Vals,Rows and Cols sequences all follow this form
Vals =Sequence
Rows =Sequence
Cols =Sequence
# The boxes list is created, with the row and column index of each square in each box Boxes=[]
for I in range(3):
for j in range(3):
Boxes += [[(Rows[3*i+k],Cols[3*j+l]) for k in range(3) for l in range(3)]]
#比如Boxes[1]表示第一行居中的那个小表格:
#Boxes[1]=[('1', '4'), ('1', '5'), ('1', '6'), ('2', '4'), ('2', '5'), ('2', '6'), ('3', '4'), ('3', '5'), ('3', '6')]
#接下来是定义问题,决策变量和目标函数,最大值 或最小值不影响结果 :
prob = LpProblem("Sudoku_Problem", LpMinimize)
# 定义729个二值决策变量,变量的名字(索引)是(Val,Row,Col)
choices = LpVariable.dicts("Choice", (Vals, Rows, Cols), 0, 1, LpInteger)
# 例如变量 Choice_4_2_9 ,它只能取0或1, 如果它是1,意味着number 4位于第2行第9列。如果它是0,则意味着第2行第9列没有4。
# 目标函数设为0, 因为我们只关心单元格是否满足约束条件。
prob += 0, "Arbitrary Objective Function"
这里需要注意的是定义729个二值决策变量,变量的索引是(Val,Row,Col)。这里的用法而前面稍微有点不同,
前面是直接传入一个list,这里传入一个tuple,tuple的每个元素是一个list,PuLP会帮我们展开。它生成的变量为:
{'1': {'1': {'1': Choice_1_1_1, '2': Choice_1_1_2, ...
这样的好处是我们可以用类似3维数组的方式来引用一个变量,比如choices[‘1’][‘2’][‘3’]。而如果我们自己构造3-tuple的list,我们只能用choices[(‘1’,’2’,’3’)]。
另外上面定义choices时指定的类型是’Integer’,上界和下界是1和0,其实可以用更加简单的’Binary’来定义:
choices = LpVariable.dicts("Choice", (Vals, Rows, Cols), cat='Binary')
首先我们来实现如下约束:81个格子对应的9个决策变量有且仅有一个为1,其余都是0。
for r in Rows:
for c in Cols:
prob += lpSum([choices[v][r][c] for v in Vals]) == 1, ""
这可以用这9个变量的和为1来表示,因为都是二值变量,它们的取值只能是0或者1。它们加起来等于1也就是有且仅有一个是1。
接下来我们约束每一行的9个数都不同:
for v in Vals:
for r in Rows:
prob += lpSum([choices[v][r][c] for c in Cols]) == 1, ""
看起来有点难懂,我们看循环的一个取值,v=’8’和r=’1’,则定义的约束是:
lpSum([choices['8']['1'][c] for c in Cols]) == 1
这是什么意思呢?它就是定义了:
[choices['8']['1']['1'] + [choices['8']['1']['2'] + ... + [choices['8']['1']['9'] == 1
隐含的意思就是第1行的9个数中有且仅有一个值为8。
类似的我们可以约束每一列的9个数都不同:
for v in Vals:
for c in Cols:
prob += lpSum([choices[v][r][c] for r in Rows]) == 1, ""
定义每个小表格的约束稍微麻烦一点:
for v in Vals:
for b in Boxes:
prob += lpSum([choices[v][r][c] for (r, c) in b]) == 1, ""
它的意思也是对于某个v,它在Box b里出现且仅出现一次。为了简洁,我们可以把这三个循环合并一下:
for v in Vals:
for r in Rows:
prob += lpSum([choices[v][r][c] for c in Cols]) == 1, ""
同理:
for c in Cols:
prob += lpSum([choices[v][r][c] for r in Rows]) == 1, ""
for b in Boxes:
prob += lpSum([choices[v][r][c] for (r, c) in b]) == 1, ""
接下来我们定义数独已经填上的格子,也就是增加如下约束:
# The starting numbers are entered as constraints
prob += choices["5"]["1"]["1"] == 1, ""
prob += choices["6"]["2"]["1"] == 1, ""
prob += choices["8"]["4"]["1"] == 1, ""
prob += choices["4"]["5"]["1"] == 1, ""
prob += choices["7"]["6"]["1"] == 1, ""
prob += choices["3"]["1"]["2"] == 1, ""
prob += choices["9"]["3"]["2"] == 1, ""
prob += choices["6"]["7"]["2"] == 1, ""
prob += choices["8"]["3"]["3"] == 1, ""
prob += choices["1"]["2"]["4"] == 1, ""
prob += choices["8"]["5"]["4"] == 1, ""
prob += choices["4"]["8"]["4"] == 1, ""
prob += choices["7"]["1"]["5"] == 1, ""
prob += choices["9"]["2"]["5"] == 1, ""
prob += choices["6"]["4"]["5"] == 1, ""
prob += choices["2"]["6"]["5"] == 1, ""
prob += choices["1"]["8"]["5"] == 1, ""
prob += choices["8"]["9"]["5"] == 1, ""
prob += choices["5"]["2"]["6"] == 1, ""
prob += choices["3"]["5"]["6"] == 1, ""
prob += choices["9"]["8"]["6"] == 1, ""
prob += choices["2"]["7"]["7"] == 1, ""
prob += choices["6"]["3"]["8"] == 1, ""
prob += choices["8"]["7"]["8"] == 1, ""
prob += choices["7"]["9"]["8"] == 1, ""
prob += choices["3"]["4"]["9"] == 1, ""
prob += choices["1"]["5"]["9"] == 1, ""
prob += choices["6"]["6"]["9"] == 1, ""
prob += choices["5"]["8"]["9"] == 1, ""
看起来很多,但是很简单,比如第一个约束choices[“5”][“1”][“1”] == 1表示的就是第1行第1列是5。
如果我们要玩一个新的数独有些,通常就是修改这些约束定义。也可以改成从一个文件读入,甚至可以做一个GUI来设置数独的初始值。
约束定义完成,剩下的就是求解了。
# The problem data is written to an .lp file
prob.writeLP("Sudoku.lp")
# The problem is solved using PuLP’s choice of Solver
prob.solve()
# The status of the solution is printed to the screen
print "Status:", LpStatus[prob.status]
求多个解
但是一个数独通常有多个解(当然也可能无解),那怎么求所有的解呢?我们可以先求一个解,然后新增一个约束,这个约束可以排除掉这个解。听起来有点trick,我们来看一下代码:
while True:
prob.solve()
print("Status:", LpStatus[prob.status])
if LpStatus[prob.status] == "Optimal":
# The solution is written to the sudokuout.txt file
for r in ROWS:
if r in [1, 4, 7]:
sudokuout.write("+-------+-------+-------+
")
for c in COLS:
for v in VALS:
if value(choices[v][r][c]) == 1:
if c in [1, 4, 7]:
sudokuout.write("| ")
sudokuout.write(str(v) + " ")
if c == 9:
sudokuout.write("|
")
sudokuout.write("+-------+-------+-------+
")
# The constraint is added that the same solution cannot be returned again
prob += lpSum([choices[v][r][c] for v in VALS for r in ROWS for c in COLS
if value(choices[v][r][c]) == 1]) <= 80
# If a new optimal solution cannot be found, we end the program
else:
break
我们用一个循环不停的求解,直到无解。如果找到一个解之后,我们就增加一个新的约束:
lpSum([choices[v][r][c] for v in VALS for r in ROWS for c in COLS
if value(choices[v][r][c]) == 1]) <= 80
这是什么意思呢?对于一个解,所有的729个choices[v][r][c]里肯定有81个1,如果两个解相同,则这81个1出现的位置相同,否则不同。如果我们要求这81个位置的和小于等于80,则说明这81个位置至少有一个不是1,则新的解肯定和这个不同。那为什么是<=80而不是<=79?因为<=79的要求太”强”了,它可能会排除掉一个新的解,这个新的解和上一个解只有一个位置不同。
+-------+-------+-------+
| 5 3 4 | 6 7 8 | 9 1 2 |
| 6 7 2 | 1 9 5 | 3 4 8 |
| 1 9 8 | 3 4 2 | 5 6 7 |
+-------+-------+-------+
| 8 5 9 | 7 6 1 | 4 2 3 |
| 4 2 6 | 8 5 3 | 7 9 1 |
| 7 1 3 | 9 2 4 | 8 5 6 |
+-------+-------+-------+
| 9 6 1 | 5 3 7 | 2 8 4 |
| 2 8 7 | 4 1 9 | 6 3 5 |
| 3 4 5 | 2 8 6 | 1 7 9 |
+-------+-------+-------+
Extra for Experts
In the above formulation we did not consider the fact that there may be multiple solutions if the sudoku problem is not well defined.
We can make our code return all the solutions by editing our code as shown after the prob.writeLP line. Essentially we are just looping over the solve statement, and each time after a successful solve, adding a constraint that the same solution cannot be used again. When there are no more solutions, our program ends.
# A file called sudokuout.txt is created/overwritten for writing to
sudokuout = open(’sudokuout.txt’,’w’)
while True:
prob.solve()
# The status of the solution is printed to the screen
print "Status:", LpStatus[prob.status]
#The solution is printed if it was deemed "optimal" i.e met the constraints
if LpStatus[prob.status] == "Optimal":
# The solution is written to the sudokuout.txt file
for r in Rows:
if r == "1" or r == "4" or r == "7":
sudokuout.write("+-------+-------+-------+
")
for c in Cols:
for v in Vals:
if value(choices[v][r][c])==1:
if c == "1" or c == "4" or c =="7": sudokuout.write("textbar[] ")
sudokuout.write(v + " ")
if c == "9":
sudokuout.write("textbar[]
")
sudokuout.write("+-------+-------+-------+
")
# The constraint is added that the same solution cannot be returned again
prob += lpSum([choices[v][r][c] for v in Vals
for r in Rows
for c in Cols
if value(vars[v][r][c])==1]) textless[]= 80
# If a new optimal solution cannot be found, we end the program
else:
break
sudokuout.close()
# The location of the solutions is give to the user print "Solutions Written to sudokuout.txt"
When using this code for sudoku problems with a large number of solutions, it could take a very long time to solve them all. To create sudoku problems with multiple solutions from unique solution sudoku problem, you can simply delete a starting number constraint. You may find that deleting several constraints will still lead to a single optimal solution but the removal of one particular constraint leads to a sudden dramatic increase in the number of solutions.