一、前置知识
二、概述
\(Pollard\_Rho\) 是一个用来寻找一个合数的因子的算法。
显然,我们可以用试除法在\(\mathcal O(\sqrt{n})\)的复杂度内完成这一操作,但我们对这个复杂度并不满意,我们需要一个更优秀的算法。
三、核心思想
事实上,我们还有一种奇妙的方法来寻找一个合数的因子:
scanf("%d",&n);
vector<int> fac;
for(int i=1;i<=???;++i){
int a=rand()%(n-1)+1;
if(n%a==0) fac.push_back(a);
}
这个代码试图通过随机一些数并判断他们是否是\(n\)的因数,毫无疑问,这是一个非常蠢的方法,因为单次操作找到\(n\)的因数的概率实在是太小了。
这个算法非常的劣质,但我们的\(Pollard_Rho\)正是基于这个算法而来的,它的核心思想就是随机。
四、优化
有一个著名的悖论叫做生日悖论,这个悖论的内容大概就是:
如果现在有\(1000\)个数,在他们中寻找到\(37\)的概率非常小,但如果我们要选2个差恰好是37的数,这个概率就会提高一倍,如果我们选择\(k\)个数,使它们中存在2个数的差恰好是37,这个概率又会大大提升,当\(k=30\)时,概率已经超过\(50%\),当\(k=100\)时,概率已经达到\(99.99%\)。
这个悖论告诉我们:寻找一些满足答案的组合会比寻找单个个体的概率更大。
我们可以利用这一点来优化上面的那个算法:
因为\(n\)的因数一定是\(n\)与某个数的最大公约数的约数,所以我们考虑寻找一个\(k\)使\(gcd(n,k)>1\),然后对\(gcd(n,k)\)递归处理。
这时候我们就可以用上生日悖论的思想,不直接寻找\(k\),而是寻找一组数\(a_i\),使他们中存在\(gcd(a_i-a_j,n)>1\)。
可以证明,这样的做法大约需要选取\(n^{\frac 14}\)个数字,\(\mathcal O(n^2)\)一一对比的话复杂度依然过高。于是我们考虑并不直接选取这么多数,而是依次生成,依次比较。
五、Pollard_Rho
这时,就有人提出了一个函数来生成这样的随机数:
其中c可以随机生成
于是我们先随机生成一个\(x_1\),再代入函数中得到\(x_2=f(x_1),x_3=f(x_2) \dots\)
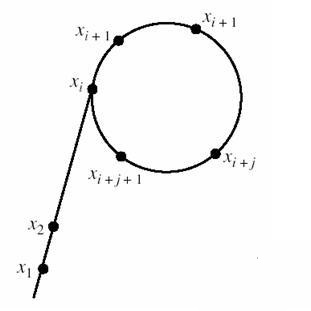
这个函数生成的随机数效果很好,但它也有一个问题,就是在有些情况下,\(f\)会在嵌套数次之后,在有一个有限数集中无限循环,它的图象大概是这样(图是盗的)
你会发现这个图形很像\(\rho\)(\(rho\)),\(Pollard \_ Rho\)因此而得名。
那么如何解决这个问题呢:直观的想法是直接记录下经过的每个数,出现循环后直接退出。
但这样做消耗的内存太大了,我们可以用\(Floyd\)的方法来判定:
假设我们有2个用\(Pollard\)函数生成的值\(a\)和\(b\),假设每嵌套一次函数都是走一步
那么我们让\(a\)每次走一步,\(b\)每次走两步,当\(a\)与\(b\)相等时,说明出现了环
六、倍增积累gcd
上面的算法已经非常精妙,但想要通过这道毒瘤的题还是有些困难
在计算时,我们将每次产生的\(abs(a-b)\)相乘并积累下来,最后直接判断这个乘积与\(n\)的gcd。
但是,如果某一时刻积累下来的样本的乘积为0了,为了不让样本丢失,我们直接退出循环进行判断即可。
每次计算是的阈值我们可以设为倍增的,并加一个上限,使用\(128\)是不错的选择。
至此,\(Pollard\_Rho\)的算法流程已经结束,这里给出上面那道例题的代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int T;
ll ans;
inline ll add(ll x,ll y,ll mod){return (x+y>=mod)?x+y-mod:x+y;}
inline ll mul(ll x,ll y,ll mod){
ll z=(long double)x/mod*y;
ll ret=(x*y-z*mod)%mod;
return (ret+mod)%mod;
}
inline ll ksm(ll x,ll y,ll mod){
ll ret=1;
for(;y;x=mul(x,x,mod),y>>=1) if(y&1) ret=mul(ret,x,mod);
return ret;
}
int pr[11]={2,3,5,7,11,13,17,19,23,29,31};
inline bool Miller_Rabin(ll n){
if(n<2) return false;
for(int i=0;i<=10;++i){
if(n==pr[i]) return true;
if(n%pr[i]==0) return false;
}
ll t=n-1,s=0;
while(!(t&1)) ++s,t>>=1;
for(int i=0;i<=10;++i){
ll a=pr[i];ll cur=ksm(a,t,n),nxt;
for(int j=0;j<s;++j,cur=nxt){
nxt=mul(cur,cur,n);
if(nxt==1&&cur!=1&&cur!=n-1) return false;
}
if(cur!=1) return false;
}return true;
}//Miller_Rabin
inline ll f(ll x,ll c,ll mod){return add(mul(x,x,mod),mod-c,mod);}//用-c在这道题目中的效率貌似更高
inline ll gcd(ll x,ll y){return y==0?x:gcd(y,x%y);}
inline ll rad(ll x){
return 1ll*rand()*rand()%x*rand()%x+1;
}
inline ll Pollard_Rho(ll n){
if(n==4) return 2;//因为一开始我们就将函数迭代了2次,所以我们无法处理n=4时的答案,需要特判
ll x=rad(n-1),c=rad(n-1),y=x;
x=f(x,c,n),y=f(x,c,n);
for(int lim=1;x!=y;lim=min(128,lim<<1)){//倍增的阈值
ll cur=1,nxt;
for(int i=1;i<lim;++i,cur=nxt){
nxt=mul(cur,abs(add(x,n-y,n)),n);
if(!nxt) break;//当nxt=0时,说明已经出现了符合条件的样本,为避免样本丢失直接退出
x=f(x,c,n);y=f(f(y,c,n),c,n);//x每次跳1步,y每次跳2步
}
ll d=gcd(cur,n);if(d!=1) return d;
}
return n;
}
inline void resolve(ll n){
ll d=Pollard_Rho(n);
while(d==n) d=Pollard_Rho(n);//寻找到一个n的因子
if(Miller_Rabin(d)) ans=max(ans,d);
else resolve(d);//如果d是质数,则直接更新答案,否则继续递归处理
if(Miller_Rabin(n/d)) ans=max(ans,n/d);
else resolve(n/d);
}
inline void work(ll n){
if(Miller_Rabin(n)){
puts("Prime");
return ;
}
ans=0;
resolve(n);
printf("%lld\n",ans);
}
int main(){
srand(time(0));
scanf("%d",&T);
while(T--){
ll n;
scanf("%lld",&n);
work(n);
}
return 0;
}