AtCoder Beginner Contest 190

传送门

C - Bowls and Dishes

暴搜，二进制枚举，复杂度(O(2^km))

#include<iostream>
#include<cstring>

using namespace std;

const int N = 110, M = 16;

int a[N], b[N], c[M], d[M];
int n, m, k;
int st[N];

int main(){
    cin >> n >> m;
    
    for(int i = 1; i <= m; i ++) cin >> a[i] >> b[i];
    
    cin >> k;
    
    for(int i = 0; i < k; i ++) cin >> c[i] >> d[i];
    
    int res = 0;
    for(int i = (1 << k) - 1; i >= 0; i --){
        for(int j = 0; j < k; j ++)
            if(i >> j & 1) st[d[j]] = 1;
            else st[c[j]] = 1;
        
        int cnt = 0;
        for(int j = 1; j <= m; j ++)
            if(st[a[j]] && st[b[j]]) cnt ++;
        
        res = max(res, cnt);
        
        memset(st, 0, sizeof st);
    }
    
    cout << res;
    
    return 0;
}

D - Staircase Sequences

根据数据范围(10^{12})可知复杂度应该为(logn,sqrt{n})级别的，从而想到求约数问题,复杂度(O(sqrt{n}))

设首项为A，末项为B，因为公差为1，那么有

[frac{(A + B)(B - A + 1)}{2}=N\ implies (A + B)(B - A + 1)=2N ]

即(A + B)和(B - A + 1)为2N的约数，设x * y = 2N

[egin{cases} A + B = x, \ B - A + 1 = yend{cases} ]

解得

[A = frac{x - y + 1}{2},B = frac{x + y - 1}{2} ]

所以只需要枚举2N的约数并计数即可。

注意：一对x和y，可能会造成不止一组A和B。

#include<iostream>
using namespace std;

#define LL long long

LL n;

int main(){
    cin >> n;
    
    n *= 2;
    
    LL res = 0;
    for(LL i = 1; i <= n / i; i ++)
        if(n % i == 0){
            LL x = i, y = n / i;
            
            if((x + y - 1 & 1) == 0){
                if((x - y + 1 & 1) == 0) res ++;
                if((y - x + 1 & 1) == 0) res ++;
            }
        }
    
    cout << res;
    
    return 0;
}

E - Magical Ornament

最短Hamilton路径的变形（不是走过所有点，而是走过集合C中的所有点），用状压dp解。

令C = {C1, C2, ..., Ck}，下图的i的二进制表示可以体现出C1,...,Ck被取到的情况，即i表示C的一个子集

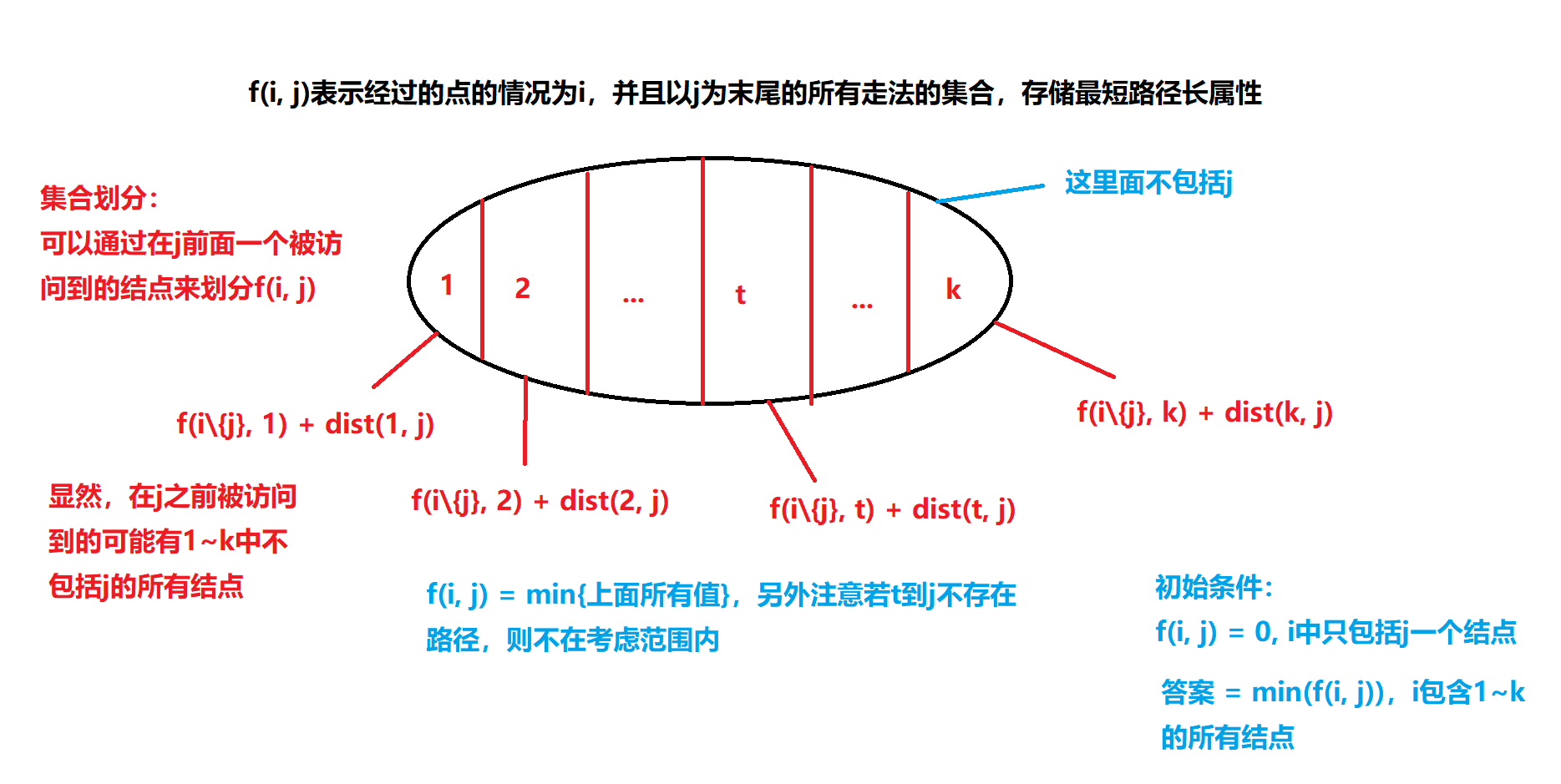
子集i的状态一共有(2^k)个，末尾点j的情况有(k)种(注意这里只是为了方便起见，实际上j的取值只有k - 1种)，状态数目 = (2^k * k), 一个状态需要k个状态参与计算，并且需要做k次bfs求距离(可以用标记数组优化，使得之前算过的可以直接返回结果，貌似全程总共做了k次的bfs)

官方复杂度：(O(2^k*k^2 + k(n + m)))

巨坑无比一个坑点：0x3f3f3f3f作为INF是不够大的。。。

另外注意：需要注意memset的复杂度为O(n)，不要随便memset。。。

还需要注意：答案要 + 1, 因为最短路径的结点数 = 最短路径长度 + 1

WA了三次的代码：

#include<iostream>
#include<vector>
#include<queue>
#include<cstring>

using namespace std;

const int K = 17, N = 100010, INF = 0x3f3f3f3f;

int n, m, k;
int c[K];
int f[(1 << K) - 1][K];

vector<int> h[N];
int st[N];
int d[K][K];

struct Node{
    int ver, level;
};

int bfs(int u, int v){
    if(~ d[u][v]) return d[u][v];
    
    memset(st, 0, sizeof st); // 这句话放这里是有原因的，它复杂度O(N)
    
    int a = c[u], b = c[v];
    
    queue<Node> q;
    q.push({a, 0});
    st[a] = 1;
    
    int res = 0;
    
    while(q.size()){
        Node t = q.front();
        q.pop();
        
        for(int i = 0; i < h[t.ver].size(); i ++){
            int j = h[t.ver][i];
            if(st[j]) continue;
            if(j == b) return d[u][v] = t.level + 1;
            
            st[j] = 1;
            q.push({j, t.level + 1});
        }
    }
    
    return d[u][v] = INF;
}

int main(){
    cin >> n >> m;
    
    while(m --){
        int a, b;
        
        cin >> a >> b;
        
        h[a].push_back(b);
        h[b].push_back(a);
    }
    
    cin >> k;
    
    for(int i = 0; i < k; i ++) cin >> c[i];
    
    memset(f, 0x3f, sizeof f);
    memset(d, -1, sizeof d);
    
    for(int i = 0; i < k; i ++) f[1 << i][i] = 0;
    
    for(int i = 1; i < 1 << k; i ++)
        for(int j = 0; j < k; j ++)
            if(i >> j & 1)
                for(int u = 0; u < k; u ++)
                    if(i - (1 << j) >> u & 1)
                        f[i][j] = min(f[i][j], f[i - (1 << j)][u] + bfs(u, j));
          
    
    int res = INF;
    for(int i = 0; i < k; i ++) res = min(res, f[(1 << k) - 1][i]);
    
    if(res == INF) puts("-1");
    else cout << res + 1;
    
    return 0;
}

把INF改为1e9以后:

#include<iostream>
#include<vector>
#include<queue>
#include<cstring>

using namespace std;

const int K = 17, N = 100010, INF = 1e9;

int n, m, k;
int c[K];
int f[(1 << K) - 1][K];

vector<int> h[N];
int st[N];
int d[K][K];

struct Node{
    int ver, level;
};

int bfs(int u, int v){
    if(~ d[u][v]) return d[u][v];
    
    memset(st, 0, sizeof st);
    
    int a = c[u], b = c[v];
    
    queue<Node> q;
    q.push({a, 0});
    st[a] = 1;
    
    int res = 0;
    
    while(q.size()){
        Node t = q.front();
        q.pop();
        
        for(int i = 0; i < h[t.ver].size(); i ++){
            int j = h[t.ver][i];
            if(st[j]) continue;
            if(j == b) return d[u][v] = t.level + 1;
            
            st[j] = 1;
            q.push({j, t.level + 1});
        }
    }
    
    return d[u][v] = INF;
}

int main(){
    cin >> n >> m;
    
    while(m --){
        int a, b;
        
        cin >> a >> b;
        
        h[a].push_back(b);
        h[b].push_back(a);
    }
    
    cin >> k;
    
    for(int i = 0; i < k; i ++) cin >> c[i];
    
    memset(d, -1, sizeof d);
    
    for(int i = 0; i < 1 << k; i ++)
        for(int j = 0; j < k; j ++)
            if(i >> j & 1){
                if(i - (1 << j)) f[i][j] = INF;
                for(int u = 0; u < k; u ++)
                    if(i - (1 << j) >> u & 1)
                        f[i][j] = min(f[i][j], f[i - (1 << j)][u] + bfs(u, j));
            }
    
    int res = INF;
    for(int i = 0; i < k; i ++) res = min(res, f[(1 << k) - 1][i]);
    
    if(res == INF) puts("-1");
    else cout << res + 1;
    
    return 0;
}

F - Shift and Inversions

求逆序对+找规律，复杂度(O(nlogn))
求逆序对可以用归并排序/树状数组
规律：

在已知第(i)个b序列的逆序对的情况下，第i + 1个b的逆序对个数可求得

因为第i + 1个b是把第i个b中的第1个元素（其实就是ai）放到最后去，形成的

由于b是0~n - 1的一个排列，所以把ai放到最后会导致损失ai个逆序对，增加(n - 1 - ai - 1 + 1 = n - 1 - ai)个逆序对，所以逆序对的变化量为(n - 1 - 2ai)

这样只需要求出序列a本身的逆序对个数，然后循环n - 1次即可。

#include<iostream>
using namespace std;

const int N = 300010;


#define LL long long

int n;
int tr[N];
int a[N];

int lowbit(int x){
    return x & -x;
}

void add(int x, int k){
    for(int i = k; i <= n; i += lowbit(i)) tr[i] += x;
}

int query(int k){
    int res = 0;
    for(int i = k; i > 0; i -= lowbit(i)) res += tr[i];
    return res;
}

int main(){
    cin >> n;
    
    for(int i = 0; i < n; i ++){
        cin >> a[i];
        a[i] ++;
    }
    
    LL res = 0;
    for(int i = 0; i < n; i ++){
        add(1, a[i]);
        res += query(n) - query(a[i]);
    }
    
    cout << res << endl;
    
    for(int i = 0; i < n - 1; i ++){
        res += n - 1 - 2 * (a[i] - 1);
        cout << res << endl;
    }
    
    return 0;
}
【推广】 免费学中医，健康全家人
原文地址：https://www.cnblogs.com/tomori/p/14377243.html