第三章回顾
随机变量引入的目的是：将随机试验的结果数量化，从而可以用 简洁的数学语言描述繁杂的随机问题，同时提高处理随机问题的效率。随机变量的 引入可以说是概率论发展中的一个重要的里程碑。
随机变量可分为散列型随机变量，连续型随机变量和非离散非连续：
- 如果随机变量 X 所有可能的取值是有限或可列多个，则称为离散型随机变量， 则其分布可表示为：
- 连续型随机变量
X是随机变量，这里的x是属于R的实数。
f(x)是密度函数=P(X<=x)，即 f(t)。
F(x)是分布函数，
。 f(t)(密度函数）从-∞到+∞求积分=1。数学含义是概率（-∞，+∞）在是1.
密度概率函数的性质：
分布函数的性质：
常见分布：
二项分布：
E(X) = np, D(X) = np(1-p)
泊松分布：
E(X)=λ，D(X)=λ
均匀分布：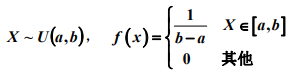
E(X) = (a+b)/2， D(X) = (b-a)^2/12
指数分布：
E(X)=1/λ，D(X)=1/λ^2
标准正太分布：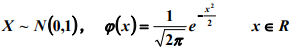
E(X)=0， D(X)=1
xa=x1-a
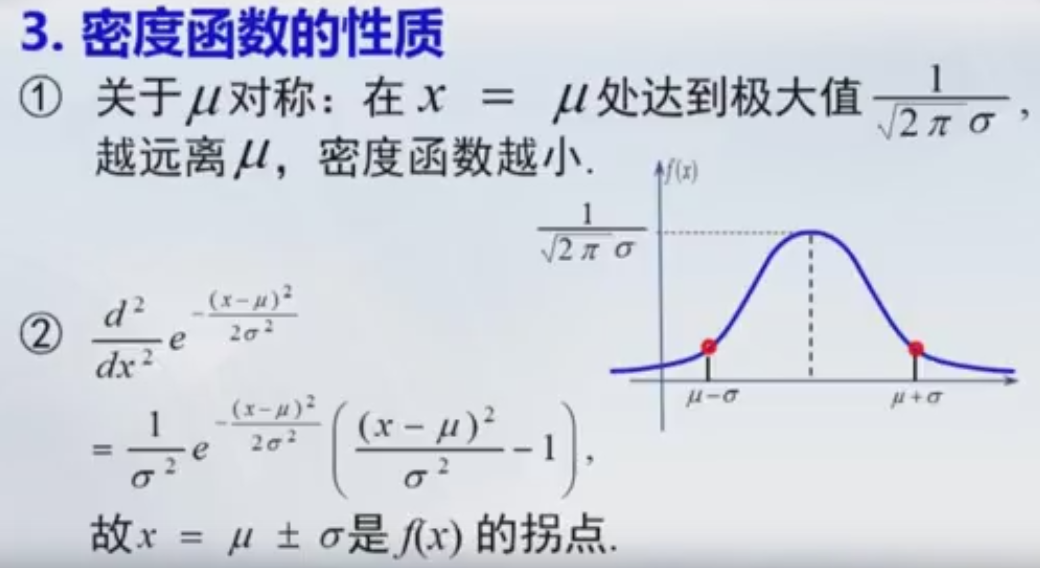
正太分布的密度函数的典型特征：
- μ是曲线的对称点，它决定曲线的中心位置，称为位置参数。
- 函数f(x)在μ处达到最大值。f(μ)=1/(2∏*σ)0.5
- 参数σ值越小，曲线显瘦，反之曲线显胖。称参数σ为形状参数。
- 当x趋于+-无穷时，limf(x)=0。
- 当μ=0，σ=1时，函数分布为标准正态分布。
正太分布是密度函数的性质：
- 密度函数是非负的。
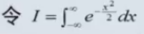，I^2 = 2∏。 I=square(2∏)- x=u+-Sigma 是f(x)的拐点。
随机变量可分为连续型随机变量，散列型随机变量和非离散非连续：
3. 1连续型随机变量：
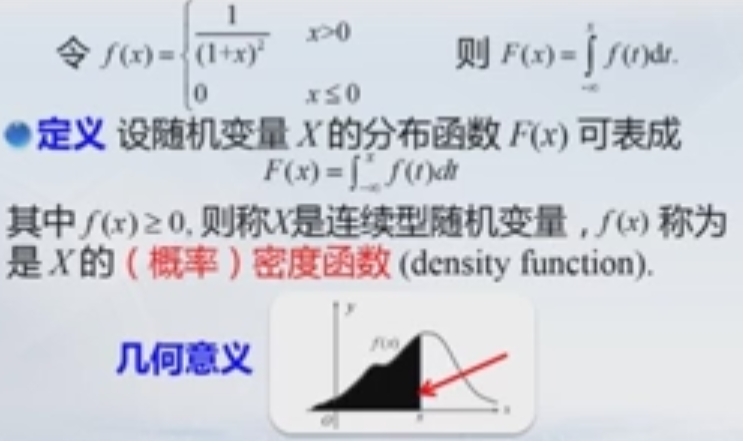
注：不可导的值是多少就是多少。可导必连续。
解：
a) x 从-∞到+∞，
，从0到1，f(x)= 
，x属于其他时，f(x)=0。=》 k=2/3
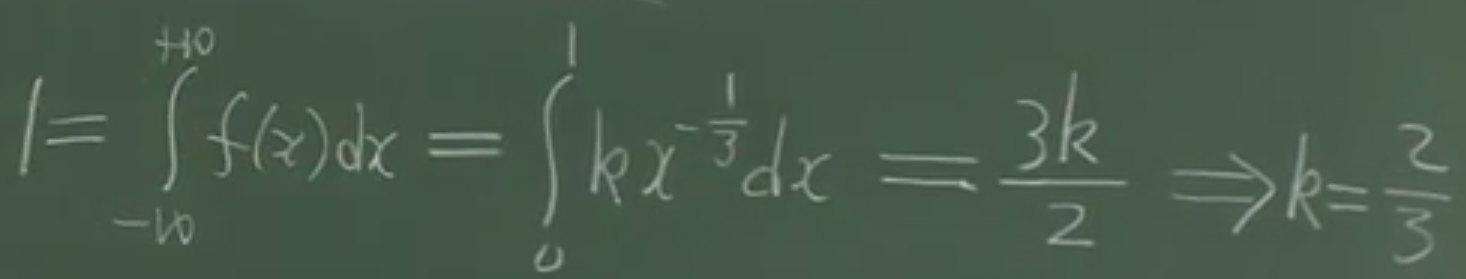即 
b) F(x)是X的分布函数，是事件（X<=x）的概率，称为X分布函数。F(x)是对f(x)求积分。
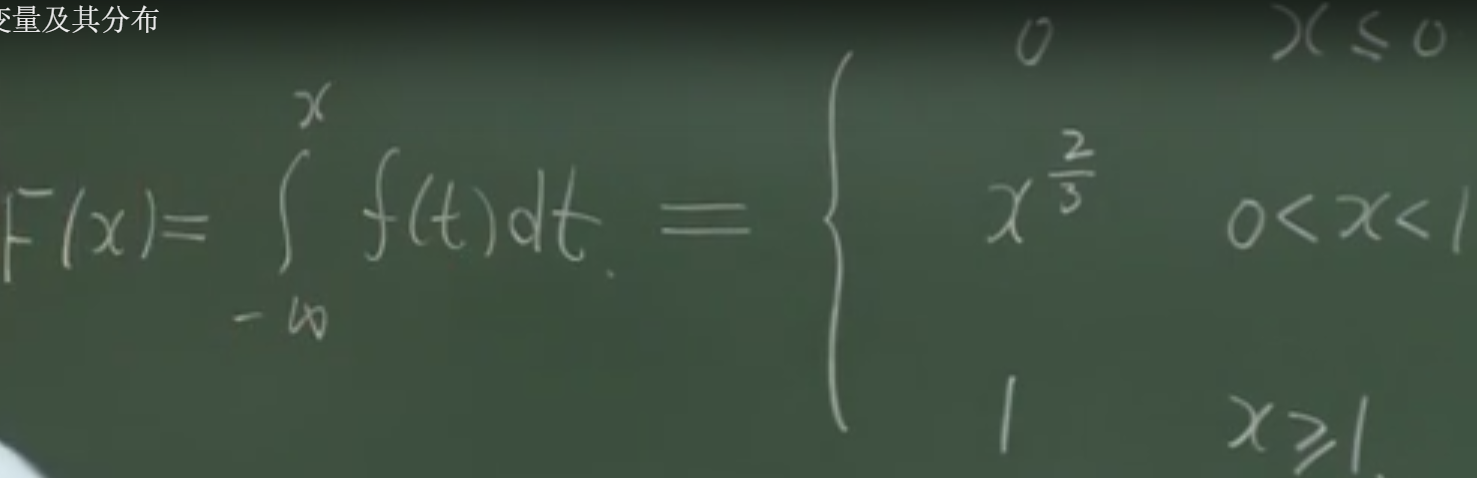
c) P{a<X<b} = F(b) - F(a)
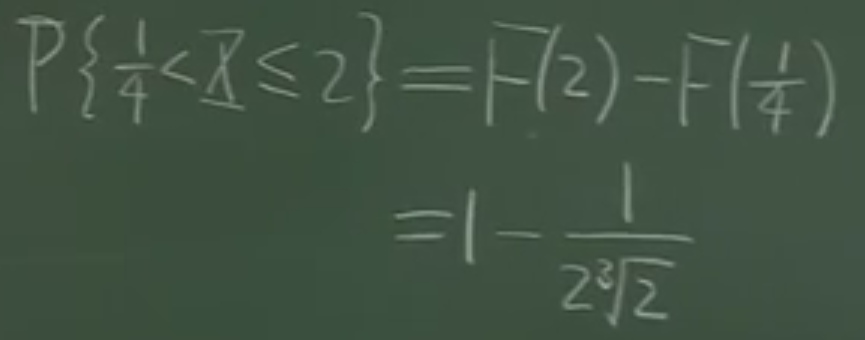
3.2 离散型随机变量
3.3 非离散非连续型随机变量
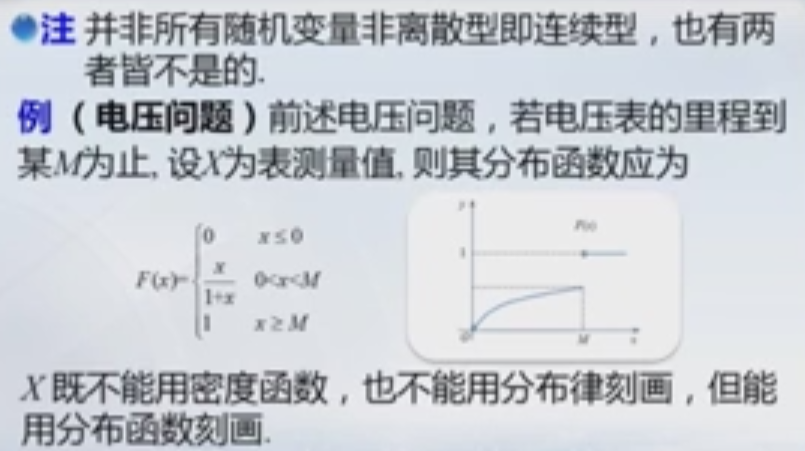
第四章 常见随机变量
1, 离散分布：（伯努利分布，二项分布，泊松分布）
将参数为 p 的伯努利试验独立地重复n次，定义随机变量 X 为试验成功的次数，则 X 的分布律为:
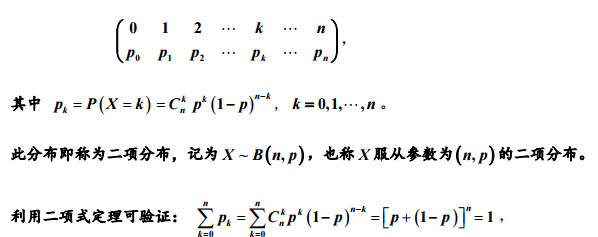
C（nk）表示抽出点数不同位置的组合。
泊松分布：放射性物质在某个时间段内，放射出的某种粒子的数量是服从这个分布。公用电话亭在某个时间段内，打电话的人数也是服从泊松分布。在一个交通路口，在一个时间段内发生交通事故的次数。
泊松分布与二项分布的关系：当n很大，而p很小时，二项分布可以近似于泊松分布。
2. 均匀分布：它的密度函数是一个常数，在区间内所有的点都是等可能的。随机变量在[a,b]区间内一个小区间的概率，只跟这个小区间的长度有关，而跟小区间的位置没有关系。
均匀分布的密度函数f(x) = 1/b-a = 常数。
1> 在1这一点左极限是等于右极限的。所以A这一点是等于1.
X属于（0，5）区间，1~3分钟的概率= P(1<=x<=3) = 2/5.
3. 指数分布与几何分布：
几何分布的无记忆性是：每次的概率都是独立的，与前面的概率无关。
F(x) = 1 - e^(-randa*x), f(x)的积分= - e^(-randa*x) + C，而0<F(x)<1，所以C= 1.
服从指数分布的变量，可以用来描述生存和寿命有关的现象。下面为指数分布密度函数和分布函数的示意图：
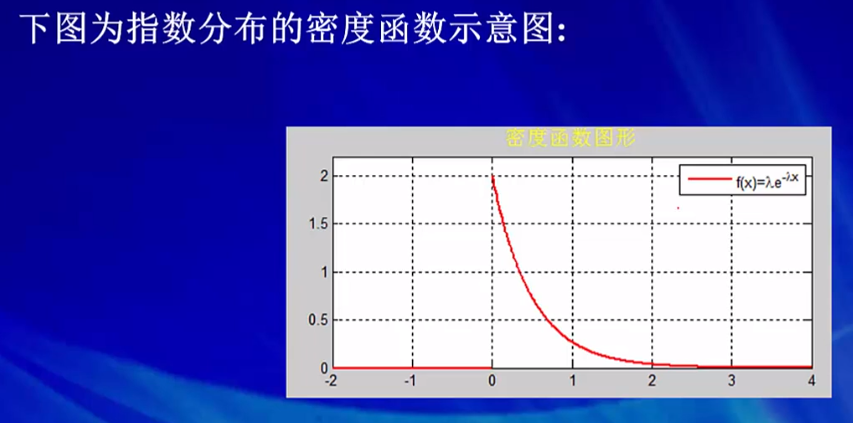
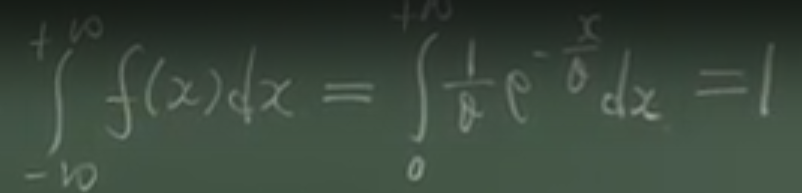
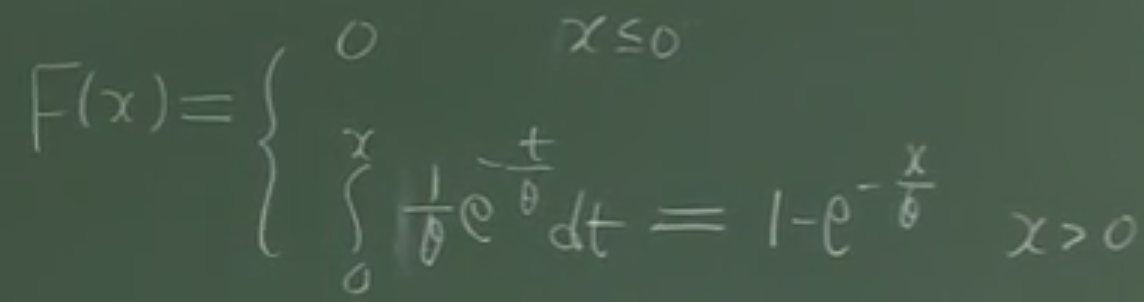
θ 的含义：x越大的地方就衰减的越厉害。（越长寿的概率越小，设备使用寿命的概率）
可以验证，指数分布也满足无记忆性的条件概率关系。而且指数分布是唯一具有无记忆 性的连续型分布。同时，几何分布是唯一具有无记忆性的离散型分布。
1> 没有得到服务离开，说明等待大于10分钟。P(x>10) = 1 - F(10)
2> 5天内没有得到服务就离开的次数服从二项分布，B(n, P) = B(5,0.135)
4. 正太分布
所有面积和等于汽车频率和，亦等于1：∑fi/δi × δi（i=1->n）= ∑fi = 1。
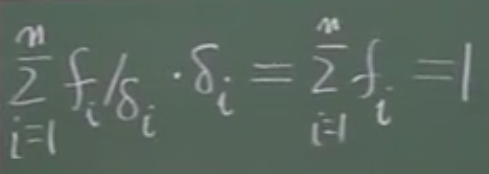
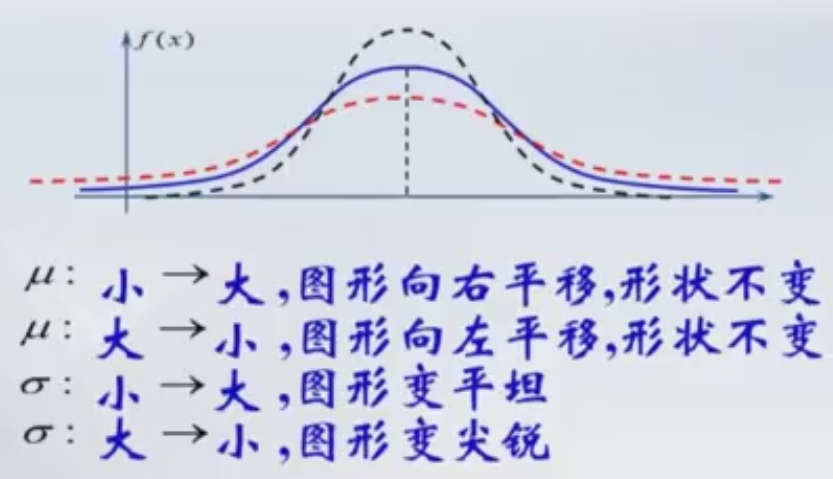
μ=0 ， 
=1时的正态分布，即 X ~ N(0,1)，称为标准正态分布。 u是位置变量，Sigma确定曲线的陡峭程度。
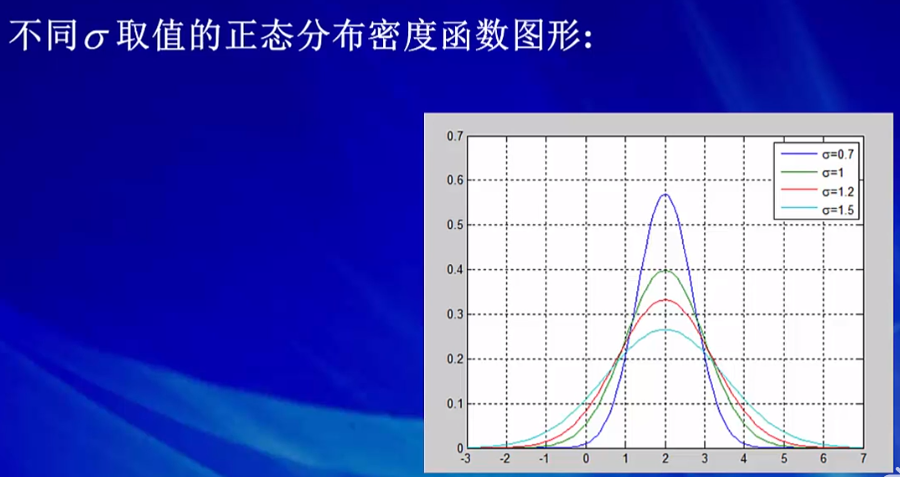
u决定了对称位置，Sigma的大小决定了曲线的陡峭程度。
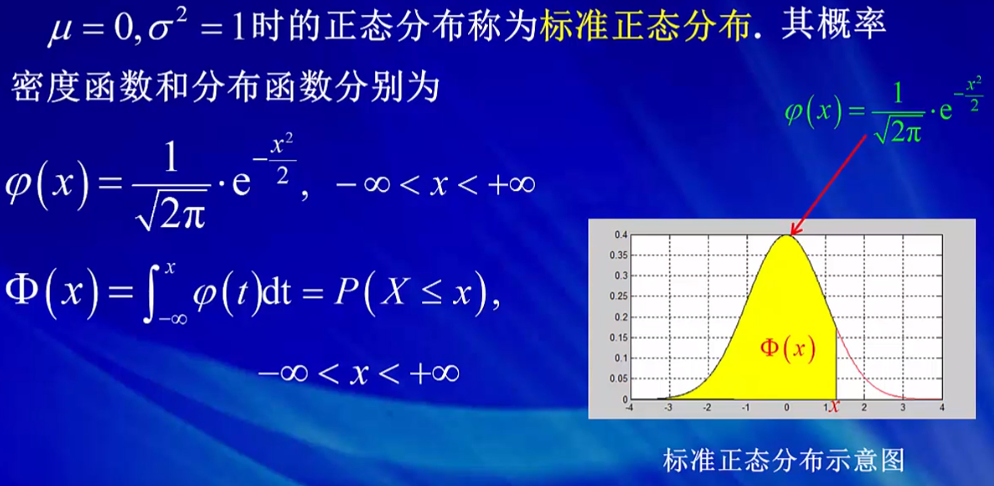
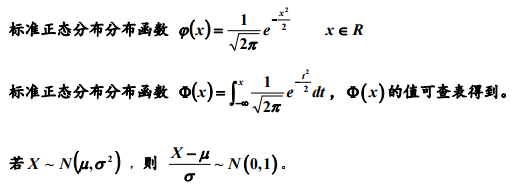
Ø(x)为密度函数
Φ(x)为分布函数
Φ(.028) = 0.6103
Φ(-0.74)=1- Φ(0.74)=1-0.7703=0.2297
正太分布是密度函数：
1. 密度函数是非负的。
2.
右图中密度函数的黑色面积部分就是这个分布函数的这点的值（X<=x,的概率）。
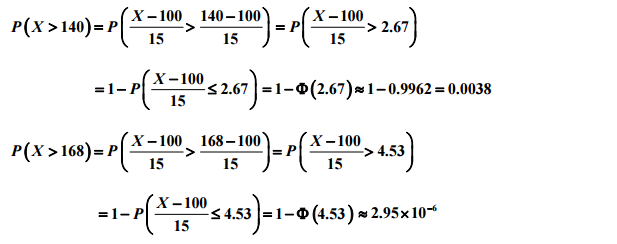
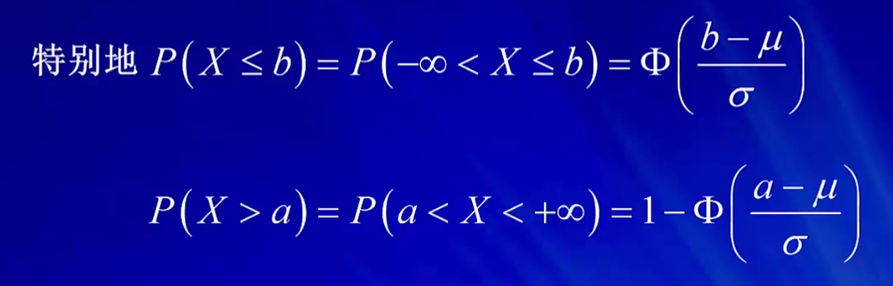
4）给定一个函数值，那么和他相对应的自变量是多少？
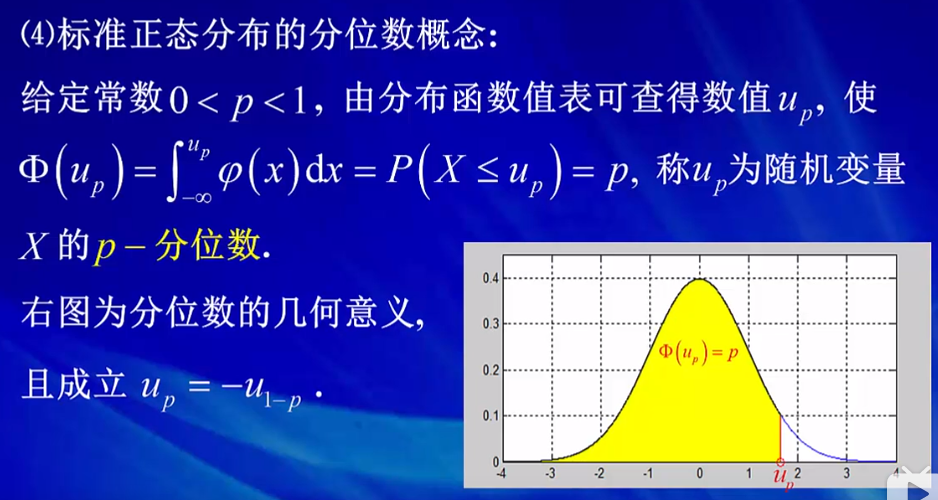
给定分位函数值为p，那么可以通过查表得出分位数up。图中黄色部分的面积为p，而横坐标上的点就是p分位数点。up=u1-p。
