EM算法要解决的问题:




隐变量问题:
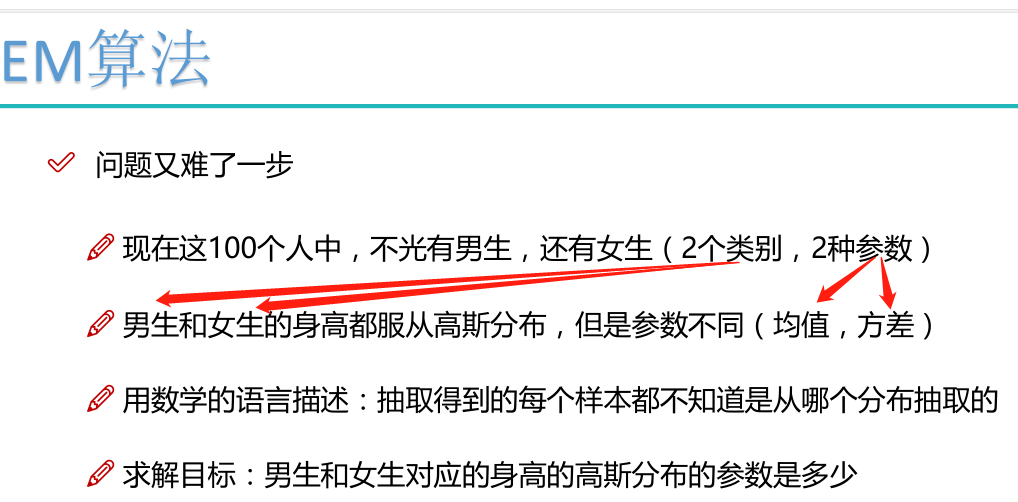

EM算法求解实例:
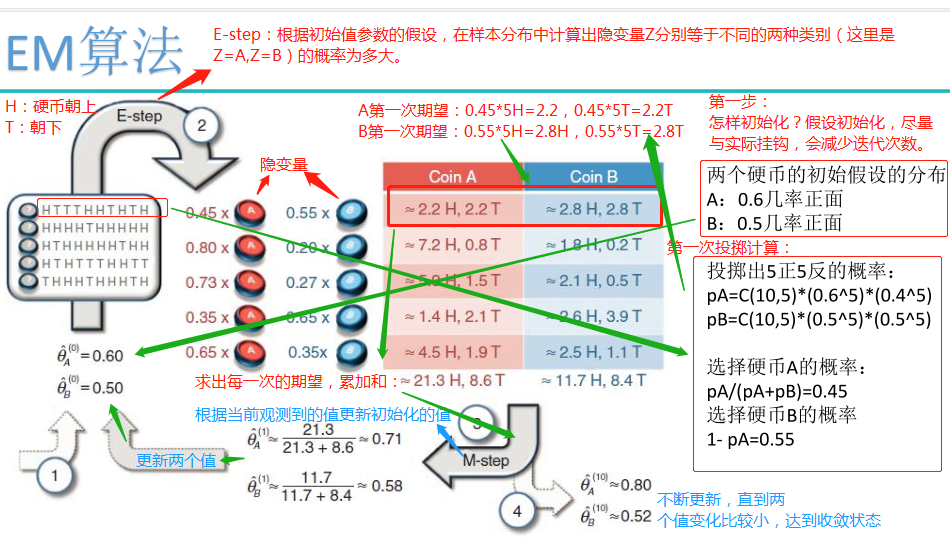
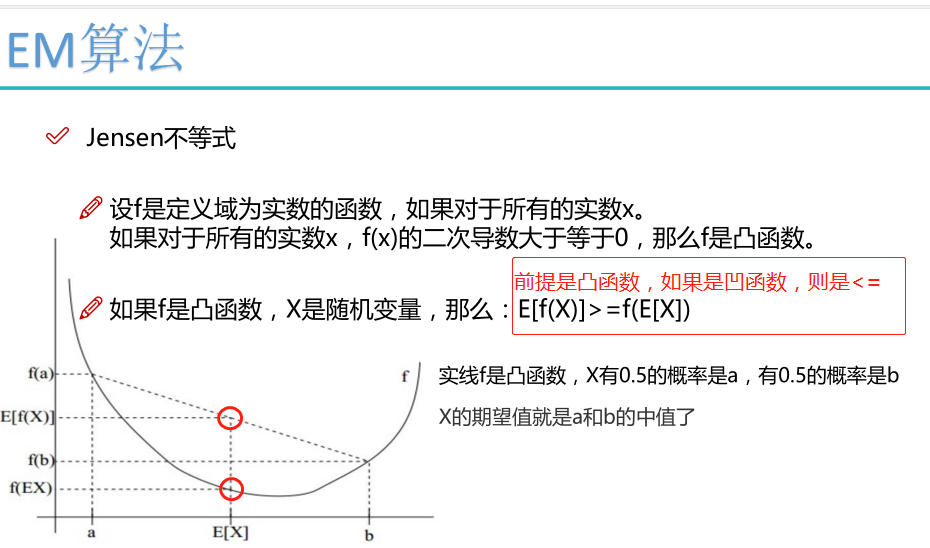
Jensen不等式:


凸函数:
如果函数f的定义域domf为凸集,且满足
∀x,y∈domf,0≤θ≤1∀x,y∈domf,0≤θ≤1有
f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)则称f为定义域上的凸函数
判定方法可利用定义法、已知结论法以及函数的二阶导数
对于实数集上的凸函数,一般的判别方法是求它的二阶导数,如果其二阶导数在区间上非负,就称为凸函数。(向下凸)
如果其二阶导数在区间上恒大于0,就称为严格凸函数。


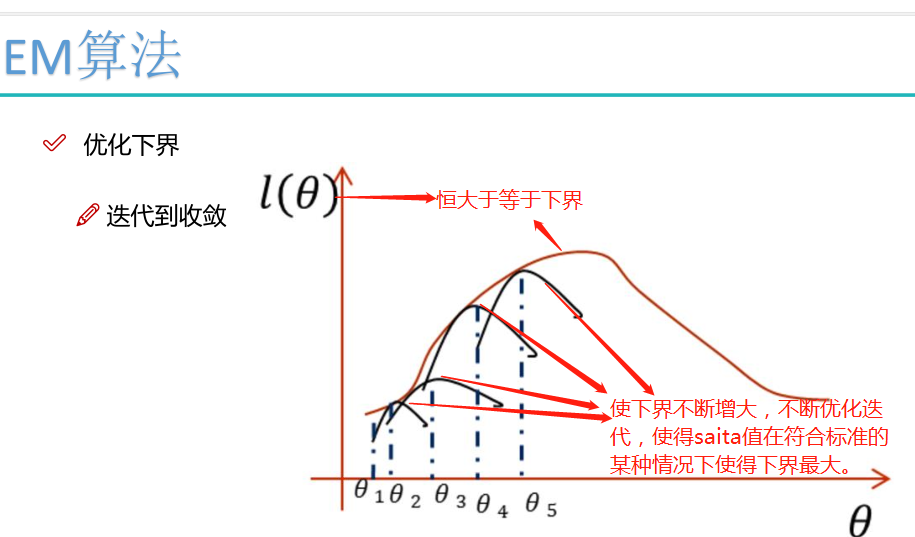



EM算法流程
初始化分布参数θ; 重复E、M步骤直到收敛:
E步骤:根据参数θ初始值或上一次迭代所得参数值来计算出隐性变量的后验概率(即隐性变量的期望),作为隐性变量的现估计值:
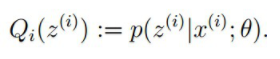
M步骤:将似然函数最大化以获得新的参数值:
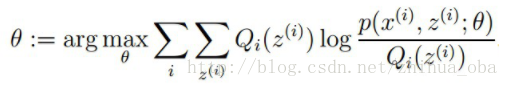

EM算法简介
EM算法是一种迭代优化策略,由于它的计算方法中每一次迭代都分两步,其中一个为期望步(E步),另一个为极大步(M步),所以算法被称为EM算法(Expectation
Maximization
Algorithm)。EM算法受到缺失思想影响,最初是为了解决数据缺失情况下的参数估计问题,其算法基础和收敛有效性等问题在Dempster,Laird和Rubin三人于1977年所做的文章Maximum
likelihood from incomplete data via the EM
algorithm中给出了详细的阐述。其基本思想是:首先根据己经给出的观测数据,估计出模型参数的值;然后再依据上一步估计出的参数值估计缺失数据的值,再根据估计出的缺失数据加上之前己经观测到的数据重新再对参数值进行估计,然后反复迭代,直至最后收敛,迭代结束。
EM算法作为一种数据添加算法,在近几十年得到迅速的发展,主要源于当前科学研究以及各方面实际应用中数据量越来越大的情况下,经常存在数据缺失或者不可用的的问题,这时候直接处理数据比较困难,而数据添加办法有很多种,常用的有神经网络拟合、添补法、卡尔曼滤波法等等,但是EM算法之所以能迅速普及主要源于它算法简单,稳定上升的步骤能非常可靠地找到“最优的收敛值”。随着理论的发展,EM算法己经不单单用在处理缺失数据的问题,运用这种思想,它所能处理的问题更加广泛。有时候缺失数据并非是真的缺少了,而是为了简化问题而采取的策略,这时EM算法被称为数据添加技术,所添加的数据通常被称为“潜在数据”,复杂的问题通过引入恰当的潜在数据,能够有效地解决我们的问题。
预备知识
极大似然估计以及Jensen不等式。
EM算法优缺点以及应用
优点:简介中已有介绍,这里不再赘述。
缺点:对初始值敏感:EM算法需要初始化参数θ,而参数θ的选择直接影响收敛效率以及能否得到全局最优解。
EM算法的应用:k-means算法是EM算法思想的体现,E步骤为聚类过程,M步骤为更新类簇中心。GMM(高斯混合模型)也是EM算法的一个应用,感兴趣的小伙伴可以查阅相关资料