机器人学——1.8-单位四元数

四元数是复数的一种扩展，或叫超复数，记作一个标量加上一个向量：
$egin{array}{rl} mathring{q}&=s+v\ &=s+v_1i+v_2j+v_3k end{array}$其中，$sinmathbb{R}$，$vinmathbb{R}^3$，正交复数 $i$，$j$，$k$ 的定义如下
$i^2=j^2=k^2=ijk=-1$我们将一个四元数表示为
$mathring{q}=s<v_1, v_2, v_3>$
早期反对四元数的一-个理由是其乘法不可交换，但正如我们在上面看到的，这种不可交换性正好符合坐标系旋转的情况。除去最初的争论不说，四元数以其格式优雅、功能强大、计算简单已被广泛应用于机器人、计算机视觉、计算机图形学以及航空航天惯性导航领域。

在机器人工具箱中，四元数是由名为Quaternion的类来实现的。构造函数将传递的参数转换为四元数，例如：

>> q = Quaternion(rpy2tr(0.1, 0.2, 0.3))
q = 
0.98186 < 0.064071, 0.091158, 0.15344 >

为了描述坐标系的旋转，我们使用单位四元数。这些四元数为一个单位大小，即 $|mathring{q}| =1$ 或 $s^2+v_1^2+v_2^2+v_3^2=1$。例如：

>> q.norm
ans =
     1

单位四元数具有一个特殊属性，它可以被看作是绕单位向量 $hat{n}$ 旋转了 $heta$ 角，该旋转与四元数组的关系为
$s=cosfrac{ heta}{2}, quad v = left(sinfrac{ heta}{2} ight)hat{n}$与绕任意向量旋转相似。
Quaternion类可以重载一些标准方法和函数。四元数的乘法通过重载乘法运算符调用：

>> q = q * q;

求一个四元数的共轭为

>> q.inv()
ans = 
0.98186 < -0.064071, -0.091158, -0.15344 >

一个四元数乘以它的逆四元数为

>> q * q.inv()
ans = 
1 < 0, 0, 0 >

或者

>> q / q
ans = 
1 < 0, 0, 0 >

得出一个单位四元数，它代表一个无效旋转。
一个四元数可以用以下方式转化为一个正交旋转矩阵:

>> q.R
ans =
    0.9363   -0.2896    0.1987
    0.3130    0.9447   -0.0978
   -0.1593    0.1538    0.9752

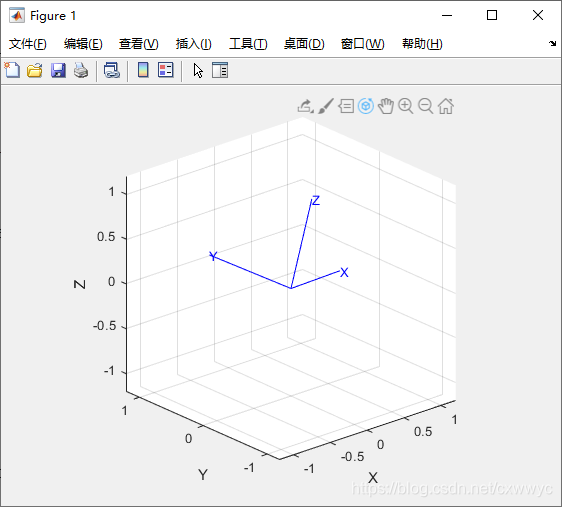
我们也可以用以下函数绘制一个四元数所指的方向：

>> q.plot()

在四元数的情况下，广义位姿是 $xi sim mathring{q} in mathbb{Q}$，且
$mathring{q_1}oplusmathring{q_2}mapsto s_1s_2-v_1cdot v_2,<s_1v_2+s_2v_1+v_1 imes v_2>$上式被称为四元数积或汉密尔顿积，并有
$ominusmathring{q}mapstomathring{q}^{-1}=s,<-v>$这是四元数的共轭。零位姿 $0mapsto1<0,0,0>$，为单位四元数。一个向量 $vinmathbb{R}^3$ 被旋转，表示为 $mathring{q}cdot vmapstomathring{q}mathring{q}(v)mathring{q}-1$，其中 $mathring{q}(v)=0, <v>$ 被称为纯四元数。

将一个三元向量传递给构造函数,将产生一个纯四元数：

>> Quaternion([1 2 3])
ans = 
0 < 1, 2, 3 >

其中的标量为 $0$。使用重载的乘法运算符，一个向量可以被一个四元数旋转：

>> q*[1 0 0]'
ans =
    0.9363
    0.3130
   -0.1593