机器人学（MATLAB机器人工具箱10.x）—

机器人学（MATLAB机器人工具箱10.x）——3.5-特殊问题

关节角偏移

机器人的零关节角位姿往往是某个很不寻常的（甚至是机械无法实现的）位姿。对于 Puma 机器人，其零角度位姿就呈现出一种不是很明显的 L 形状，机器人的上臂水平，下臂垂直向上，如图所示。
在这里插入图片描述
这一结果是由机器人的 D-H 参数形式所决定的。机器人的控制设计人员可能会选择零关节角位姿为一些更为明显的位形。关节坐标偏移提供了一种机制，它使我们可以设置任意位形作为零关节坐标。偏移向量 $q_0$ 要在任何运动学或动力学函数被调用之前被加到用户指定的关节角度上。例如：
$xi=mathcal{K}(q+q_0)$
类似地，它要在执行一次运算操作后被减去，如逆运动学：
$q = mathcal{K}^{-1}(xi)-q_0$
偏移量设置是通过设定Link对象的offset属性来完成的。例如：

>> L = Link([0 0 1 0]);
>> L.offset = pi/4
 
L = 
Revolute(std): theta=q, d=0, a=1, alpha=0, offset=0.785398

或者

>> p560.links(2).offset = pi/2

如图所示
在这里插入图片描述

确定 D-H 参数

确定 D-H 参数的经典方法是系统地为每个连杆分配一个坐标系。Puma 机器人的连杆坐标系就是采用标准 D-H 形式进行设定的，如图所示。
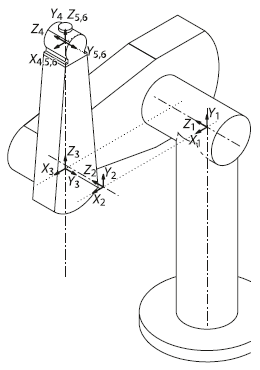
在这里插入图片描述
然而，每一个坐标系都有很强的约束，因为关节旋转必须围绕 $z$ 轴，连杆位移必须沿 $x$ 方向。这也为基座和末端执行器坐标系的设定施加了约束，进而最终决定了前面讨论的零角度位姿。因此为一个全新的机械臂确定 D-H 参数和连杆坐标系要比想象的困难。
工具箱还支持另一种方法，它简单地将机械臂描述为一系列从末端执行器基座到顶端的基本平移和旋转。有些基本操作是常数，如表示连杆长度或偏移量的平移，而一些操作是广义关节坐标 $q_i$ 的函数。不同于传统的方法，我们不对这些有可能发生旋转和平移的轴施加任何约束。
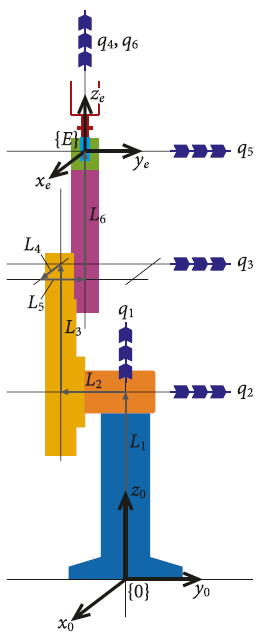
在这里插入图片描述
如上图所示的一个例子，我们首先在基座上随便定义一个坐标系，然后把从基座到顶端的平移和旋转序列写入一个字符串：

>>  s = 'Tz(L1) Rz(q1) Ry(q2) Ty(L2) Tz(L3) Ry(q3) Tx(L4) Ty(L5) Tz(L6) Rz(q4) Ry(q5) Rz(q6)'

请注意，我们已经将第二关节描述为Ry(q2)，即绕 $y$ 轴的旋转，它不能使用 D-H 形式。
该字符串被输入一个符号代数函数：

>> dh = DHFactor(s);

它返回一个 DHFactor 对象，其中保存了已被分解为 D-H 参数的机器人运动学结构。我们可以将该结构以一种可读形式显示出来：

>> dh
dh =
DH(q1, L1, 0, -90).DH(q2+90, 0, -L3, 0).DH(q3-90, L2+L5, L4, 90).DH(q4, L6, 0, -90).DH(q5, 0, 0, 90).DH(q6, 0, 0, 0)

其显示的各关节 D-H 参数顺序分别为 $heta$ ， $d$ ， $a$ 和 $alpha$ 。关节角偏移量（一个加到或减去的常量，相对于从关节角变量，如 $q_2$ 和 $q_3$ ）是自动生成的，基座和工具变换也是自动生成的。这个对象还可以生成一个字符串，它是一个工具箱命令，用于创建一个名为“puma”的机器人：

>> cmd = dh.command('puma');
>> cmd
cmd =
SerialLink([0, L1, 0, -pi/2, 0; 0, 0, -L3, 0, 0; 0, L2+L5, L4, pi/2, 0; 0, L6, 0, -pi/2, 0; 0, 0, 0, pi/2, 0; 0, 0, 0, 0, 0; ], 'name', 'puma', 'base', eye(4,4), 'tool', eye(4,4), 'offset', [0 pi/2 -pi/2 0 0 0 ])

当定义了L1到L6后，这个命令可以被执行：

>> robot = eval(cmd);

它创建一个名为robot的工作空间变量，该变量是一个SerialLink对象。

改进型 D-H 参数

1986年，克雷格[Craig 1986]首先提出了一种改进的 D-H 参数，如图所示
在这里插入图片描述

其中每个连杆坐标系被固接到该连杆的近端（靠近前一个连杆），而不是其远端。经过这种修改，使得参数符号在某些方面显得更加清晰和简洁，因而目前这种 D-H 参数法也更为常用。然而它的引入也增加了更多的混乱，特别是对那些机器人运动学的初学者。该问题的根源在于运动学、雅可比矩阵和动力学的算法都是依赖于其使用的运动学约定。根据克雷格的约定，连杆变换矩阵是
$^{j-1}A_j=R_x(alpha_{j-1})T_x(a_{j-1})R_z( heta_j)T_z(d_j)$
克雷格将其表示为 ${}_{j}^{j-1}A$ 。它与上述方程具有相同的因子项，但是顺序不同——记住旋转顺序是不可交换的，而这正是问题的核心。 $a_j$ 始终表示连杆 $j$ 的长度，但在一种约定中它是坐标系 ${j}$ 和 ${j+1}$ 之间原点的位移，而在另一种约定里它又变成坐标系 ${j-1}$ 和 ${j}$ 之间的原点位移。

一般看论文的时候，弄清楚该作者所使用的 D-H 约定尤其重要，但这一重要信息往往不被提及。你可以从表格的栏标题上寻找线索。如果它们都具有相同的下标，即 $heta_j$ ， $d_j$ ， $a_j$ 和 $alpha_j$ ，那么它是标准 D-H 参数法。如果有一半的下标是不同的，即 $heta_j$ ， $d_j$ ， $a_{j-1}$ 和 $alpha_{j-1}$ ，那么你正在使用改进 D-H 参数法。总之，你必须知道你的 D-H 参数属于何种运动学约定。
当然，如果在你发表的论文中能清楚地说明你的参数使用何种运动学约定，那对读者肯定会有所帮助。

工具箱对于两种参数形式都可以处理。对于改进 D-H 参数法，只需要在创建连杆对象时增加一个可选参数来指定：

>> L1 = Link([0 1 0 0 0], 'modified')
L1 = 
Revolute(mod): theta=q, d=1, a=0, alpha=0, offset=0

或

>> L1 = RevoluteMDH('d', 1)
L1 = 
Revolute(mod): theta=q, d=1, a=0, alpha=0, offset=0

而标准 D-H 参数为

>> L1 = Link([0 1 0 0 0])
L1 = 
Revolute(std): theta=q, d=1, a=0, alpha=0, offset=0

或

>> L1 = Revolute('d', 1)
L1 = 
Revolute(std): theta=q, d=1, a=0, alpha=0, offset=0

如：
$underset{ ext{DH}_1}{underbrace{T_{Rz}left( heta _1 ight) T_zleft( d_1 ight) T_xleft( a_1 ight) T_{Rx}left( alpha _1 ight) }}underset{ ext{DH}_2}{underbrace{T_{Rz}left( heta _2 ight) T_zleft( d_2 ight) T_xleft( a_2 ight) T_{Rx}left( alpha _2 ight) }}cdots$
可以将其重新组合为
$underset{ ext{base}}{underbrace{T_{Rz}left( heta _1 ight) T_zleft( d_1 ight) }}underset{ ext{MDH}_1}{underbrace{T_xleft( a_1 ight) T_{Rx}left( alpha _1 ight) T_{Rz}left( heta _2 ight) T_zleft( d_2 ight) }}underset{ ext{MDH}_2}{underbrace{T_xleft( a_2 ight) T_{Rx}left( alpha _2 ight) cdots }}$
其中标记为 $ext{MDH}_j$ 的一项具有与最开始所说的连杆变换矩阵相同的形式，因为关于同一轴的平移和旋转是可以交换顺序的，即 $T_{Rk}( heta)T_k(d)=T_k(d)T_{Rk}( heta)$ ，其中 $kin{x,y,z}$ 。