[HNOI2008]玩具装箱TOY

"这是一道经典的斜率优化入门题,就用这题来作个总结好了."
这道题用到的是单调队列(我只会这玩意儿)的斜率优化.
我们整理一下题意会发现它的状态转移方程就是下面这东西:

[dp[i]=min(dp[j]+(sum[i]+i-sum[j]-j-L-1)^2),i>j ]

上面这张图讲得已经很清楚了.
我们如果把含(j)的相关变量都看成点的坐标的话,此时我们要做的就是尽量让截距更小.
怎么让截距最小呢?难道一个一个比较吗?
我们再来看下面这张图:

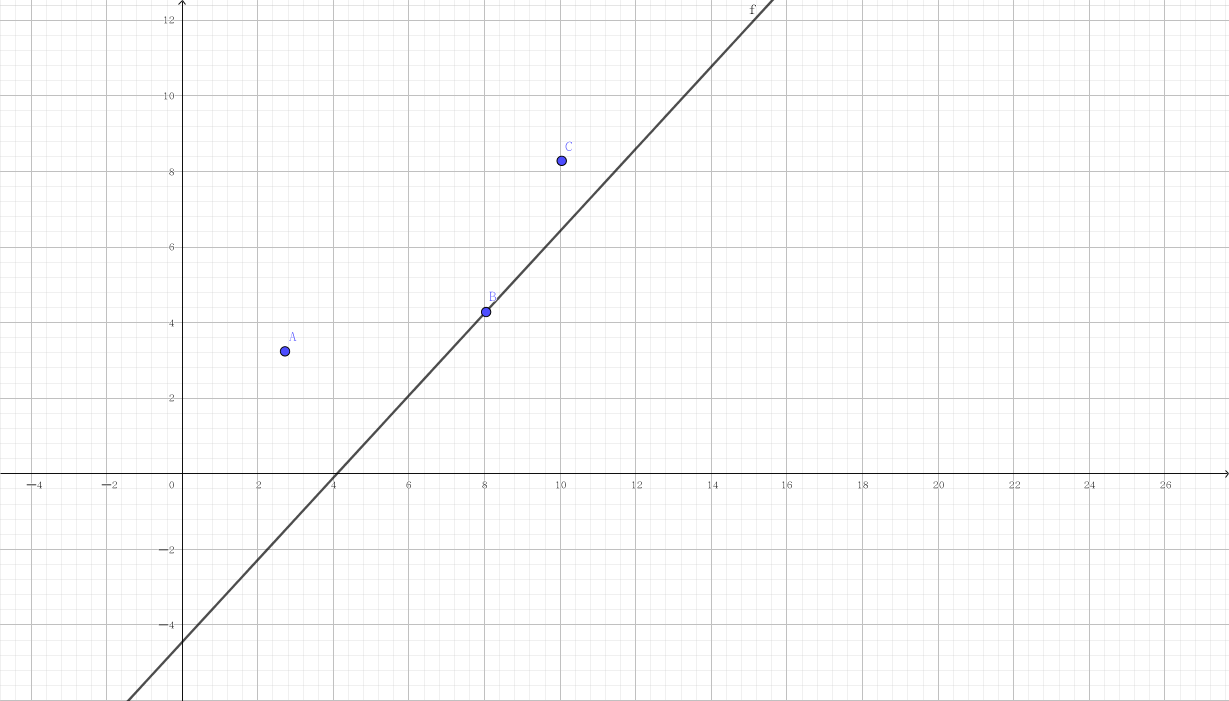
上面三个点是我们可供选择的三个点,这条直线就是我们就是要使这条一直斜率的截距最小.
高中数学学线性规划的时候我们都知道,显然是选途中的(B)点.
那么对于这一条直线,我们根据斜率和坐标可以计算截距,从而得到dp值.
那剩下两个点呢?
对于(A)点,我们是不是可以丢掉它了?是的,由于我们的斜率是不断增大的,(A)点是不可能用来转移后面的状态了,所以把它剔除.
还有(C)点,当斜率到达一定大小,例如下图:

此时我们就要用到(C),而(B)又可以剔除.
于是我们只要维护一个凸包,而且这个凸包相邻两个点连的斜率要大于当前这条线的斜率.就像刚刚这个例子一样.一旦最左端的一个点和次左端的点的连线要小于当前的斜率了,就把最左端的点剔除.
这样每次遇到新的直线,直接拿最左端的点(队头)来转移,加入一个新点就加到最右边(队尾),因为横坐标也是递增的.再加入这个点之前,我们一定要保证下凸的性质,例如下面这个例子:

(B)显然要被剔除.
为什么一定维护凸包呢?为什么一定是弹掉(B).(C)为什么更优呢?自己想象一下,一条直线斜率大于(CG)的直线从下面平移上来,走啊走,最后一定会在(C)这里停下.如果是一条斜率小于(GC)大于(GF)的,显然会在(G)停下,这样(B)就没有人和用武之地了.

在这里我们总结一下,单调队列斜率优化的步骤:
1.弹队头,就是最左边的点.
2.放直线,算答案,得到当前状态的答案,得到新的待加入的点.
3.弹队尾,把插入新点之后不合法的点弹掉.最后加入新点就好了.

代码:

#include<iostream>
#include<cstdio>
#include<cmath>
#define maxn 50005
#define ll long long
using namespace std;
int q[maxn];
double A[maxn],B[maxn],dp[maxn],sum[maxn];
double X(int x){return B[x];}
double Y(int x){return dp[x]+B[x]*B[x];}
double slope(int a,int b){return (Y(a)-Y(b))/(X(a)-X(b));}
int main()
{
	int n,l;cin>>n>>l;
	for(int i=1;i<=n;i++)scanf("%lf",&sum[i]);
	for(int i=1;i<=n;i++)
	{
		sum[i]+=sum[i-1];
		A[i]=sum[i]+i;B[i]=sum[i]+i+l+1;
	}
	B[0]=l+1;//B[0]=sum[0]+0+l+1=l+1
	int tail=1,head=1;
	for(int i=1;i<=n;i++)
	{
		while(head<tail&&slope(q[head],q[head+1])<2*A[i])head++;
		int j=q[head];dp[i]=dp[j]+(A[i]-B[j])*(A[i]-B[j]);
        //why:dp[j]+B^2=2*A*B-A^2+dp[i];
		//    dp[i]=dp[j]+A^2+B^2-2*A*B=dp[j]+(A-B)(A-B)
		while(head<tail&&slope(i,q[tail-1])<slope(q[tail-1],q[tail]))tail--;
		q[++tail]=i;
	}
	printf("%lld",(ll)dp[n]);
	return 0;
}