题意:
一颗 (n) 个节点的树,上面有 (K) 个关键点,经过每一条边都需要一定权值,求 ([1,n]) 中从每一个点出发,经过所有关键点,不用回到原点,所经过路径的最小权值和。
数据范围:
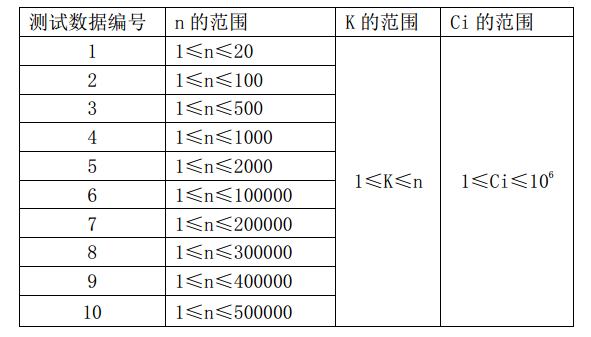
50分:(O(n^2))
-
考虑最后要回到源点的情况,那么就是每一条需要走的边都要经过两次,无论你怎么走都是一样的。所以只需要求出所有需要走的边的和,和当前源点到某一个关键点的最长路径,相减即可(减掉最后一次回来的路程)。
-
当前源点到某一个关键点的最长路径很好求,(dfs) 一次就好了。

如图,蓝点为当前源点,红点为关键点。
-
所谓需要走的边,就是图中的粗边,通过观察可以发现,一条边为粗边,当且仅当这条边连接的儿子的子树中有关键点。
-
所以只需求出以每个点为源点时每个子树里关键点的 (cnt) ,遍历到的时候统计一下就好了。时间复杂度 (O(n^2))
关键代码:
struct cut1{
int s[2005],dp[2005],mark[2005],suml,mx;
void dfs(int x,int f,int d){
if(mark[x]&&d>mx)mx=d;//求最长路径
if(mark[x])dp[x]=1;
for(int i=0;i<edge[x].size();i++){
int y=edge[x][i].to,z=edge[x][i].v;
if(y==f)continue;
dfs(y,x,d+z);
if(dp[y]!=0)suml+=z;//统计所有要走到的边
dp[x]+=dp[y];
}
}
void solve(){
for(int i=1,x;i<=k;i++){
scanf("%d",&x);//输入关键点
mark[x]=1;
}
for(int i=1;i<=n;i++){
memset(dp,0,sizeof(dp));
suml=0;mx=0;
dfs(i,0,0);
printf("%d
",suml*2-mx);
}
}
}P50;
100分:(O(m)) 从50分的思路延伸而来
和50分一样,有两个主要的问题:
-
求出每个点到某一个关键点的最长路径
-
求出每个点遍历时要经过的边(粗边和)
对于第二个问题,一篇题解已经解释的很好了。。。
定义以 (x) 为根的粗边和为 (sum[x]),(y) 为 (x) 的儿子,可以分以下三类讨论:


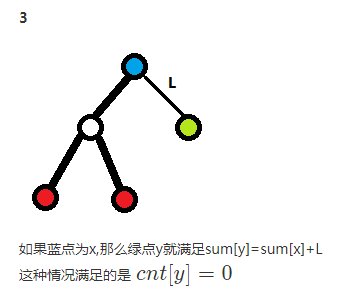
具体细节可以参考代码。
至于第一个问题,听说非常经典,我听都没听过,思路就是树形DP
每个节点记下它到它子树中关键点路径的最长值和次长值。
这个比较好实现,一次 (dfs) 即可。
注意:这个最长值和次长值并不是严格意义上的,而是对于每一个节点,从它的两个不同儿子中传来的。具体原因后面会解释。

我们把一个点到关键点的最长路径分成两部分讨论:到子树内的关键点和到子树外的关键点。
分开处理,详见代码:
#include<bits/stdc++.h>
#define debug(a) cout<<#a<<"="<<a<<endl
#define LL long long
using namespace std;
bool cur1;
const LL N=500005,inf=1e9;
struct node{LL to,v;};
vector<node>edge[N];
LL n,K;
LL mx[N][2],mxf[N],cnt[N],sum[N],tmx[N],st[N],top,fa[N],mark[N];
void dfs(LL x,LL f){
fa[x]=f;mx[x][0]=mx[x][1]=mxf[x]=-inf;
if(mark[x]){
mx[x][0]=0;
cnt[x]=1;
}
st[++top]=x;
for(LL i=0;i<edge[x].size();i++){
LL y=edge[x][i].to,z=edge[x][i].v;
if(y==f)continue;
dfs(y,x);
cnt[x]+=cnt[y];
if(cnt[y]){
sum[1]+=z;
LL nw=mx[y][0]+z;
if(nw>=mx[x][0]){
tmx[x]=y;
mx[x][1]=mx[x][0];
mx[x][0]=nw;
}
else if(nw>mx[x][1])mx[x][1]=nw;
}
}
}
void solve(){
for(LL i=1;i<=n;i++){
LL x=st[i];
for(LL j=0;j<edge[x].size();j++){
LL y=edge[x][j].to,z=edge[x][j].v;
if(y==fa[x])continue;
if(cnt[y]==K)sum[y]=sum[x]-z;
else if(cnt[y]==0)sum[y]=sum[x]+z;
else sum[y]=sum[x];
if(tmx[x]==y)mxf[y]=max(mxf[x],mx[x][1])+z;
else mxf[y]=max(mxf[x],mx[x][0])+z;
}
}
for(LL i=1;i<=n;i++)
printf("%lld
",sum[i]*2-max(mxf[i],mx[i][0]));
}
bool cur2;
int main(){
scanf("%lld%lld",&n,&K);
for(LL i=1,x,y,z;i<n;i++){
scanf("%lld%lld%lld",&x,&y,&z);
edge[x].push_back(node<%y,z%>);
edge[y].push_back(node<%x,z%>);
}
for(LL i=1,x;i<=K;i++){
scanf("%lld",&x);
mark[x]=1;
}
dfs(1,0);
solve();
return 0;
}