0.PTA得分截图

1.本周学习总结
1.1 总结图内容
图的存储结构:邻接表和邻接矩阵
邻接矩阵及其特点

1.无向图的邻接矩阵是对称的,有向图的可能是不对称的
2.对角线上的点的值都为0
3.时间复杂度和空间复杂度都为O(n^2)
4.在无向图中,统计第i行(列)1的个数可得顶点i的度。
在有向图中,统计第i行1的个数可得顶点i的出度OD;统计第j列1的个数可得顶点j的入度ID;
5.一个图的邻接矩阵是唯一的
邻接表及其特点
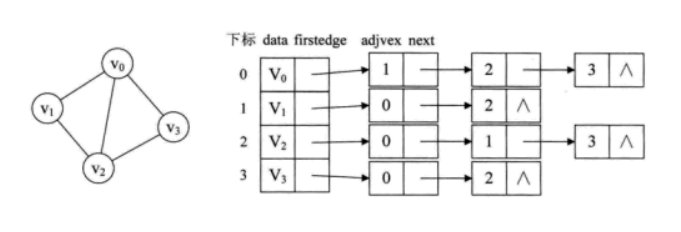
1.每条链上的其他节点都与头节点相连
2.下边为i的元素表示顶点为i的表头节点
3.图的邻接表存储方法是一种顺序分配与链式分配相结合的存储方法。
4.一个图的邻接表是不唯一的
邻接表存储类型定义: 邻接矩阵存储类型:
typedef struct ANode typedef struct
{ {
int adjvex; //该边的终点边号 int edges[MAXV][MAXV];//邻接矩阵
struct ANode*nextarc; //指向下条边的指针 int n,e;
int info; //权值 }AdjGraph;
}ArcNode;
typedef struct Vnode
{
int data;//顶点
ArcNode* firstarc;//指向第一条边
}VNode;
typedef VNode Adjlist[MAXV];
typedef struct
{
Adjlist adjlist;//邻接表
int n,e;
}AdjGraph;
图的遍历及其应用
深度遍历
含义:首先访问初始顶点v,选择一个与初始顶点相邻且没被访问过的顶点w,再从w进行深度搜索,直到所有顶点都被访问
邻接表深度遍历 邻接矩阵深度遍历
void DFS(AdjGraph* G, int v) void DFS(MGraph g, int v)
{ {
ArcNode* p; visited[v]=1;
visited[v] = 1; cout<<v;
cout<<v;
for(int j=1;j<=g.n;j++)
p = G->adjlist[v].firstarc; if(g.edges[v][j]!=0&&visited[j]==0)
while (p != NULL) DFS(g,j);
{ }
if (visited[p->adjvex] == 0)
DFS(G, p->adjvex);
p = p->nextarc;
}
}
判断从u到v是否有路径 输出从u到v的路径
void ExistPath(AGraph*G,int u,int v,bool&has) void FindaPath(AGraph*G,int u ,int v,int path[],int d)
{ {
ArcNode*p; ArcNode*p;int i;
visited[u]=1; visited[u]=1;d++;
if(u==v) path[d]=u;
{ if(u==v)
has=true; {
return; cout<<"一条路径为:";
} for(i=0;i<=d;i++)
p=G.adjlist[u].firstarc; cout<<path[i];
while(p!=NULL) return;
{ }
if(visited[p->adjvex]==0) p=G.adjlist[u].firstarc;
ExistPath(G,p->adjvex,v,has); while(p!=NULL)
p=p->nextarc; {
} if(visited[p->adjvex]==0)
} ExistPath(G,p->adjvex,v,path,d);
p=p->nextarc;
}
}
最短路径 判断图是否连通
void ShortPath(AdjGraph *G,int u,int v) int judge(AGraph g)
{ {
qu[rear].data=u;//第一个顶点u进队 for(int i=0;i<g.n;i++)
while (front!=rear)//队不空循环 visited[i]=0;
{ front++; DFS(G,0)
w=qu[front].data; for(int i=0;i<g.n;i++)
if (w==v) 根据parent关系输出路径break; if(!visited[i])//有节点没访问
while(遍历邻接表) return 0;
{ rear++; }
qu[rear].data=p->adjvex;
qu[rear].parent=front;
}
}
}
最小生成树相关算法及应用
概念:一个连通图的生成树是一个极小连通子图,它含有图中全部n个顶点和构成一棵树的(n-1)条边。不能回路。
prime算法求最小生成树
(1)初始化U={v}。v到其他顶点的所有边为候选边;
(2)重复以下步骤n-1次,使得其他n-1个顶点被加入到U中:
1.从候选边中挑选权值最小的边输出,设该边在V-U中的顶点是k,将k加入U中;
2.考察当前V-U中的所有顶点j,修改候选边:若(j,k)的权值小于原来和顶点k关联的候选边,则用(k,j)取代后者作为候选边。

克鲁斯卡尔算法求最小生成树
(1)置U的初值等于V(即包含有G中的全部顶点),TE的初值为空集(即图T中每一个顶点都构成一个连通分量)。
(2)将图G中的边按权值从小到大的顺序依次选取:
1.若选取的边未使生成树T形成回路,则加入TE;
2. 否则舍弃,直到TE中包含(n-1)条边为止。
Kruskal算法

最短路径相关算法及应用
用迪杰斯特拉(Dijkstra)算法求最短路径
初始化dist数组、path数组、s数组
遍历图中所有节点
{
for(i=0;i<g.n;i++) //找最短dist
{
若s[i]!=0,则dist数组找最短路径,顶点为u
}
s[u]=1 //加入集合S,顶点已选
for(i=0;i<g.n;i++) //修正dist
{
若s[i]!=0 && dist[i]>dist[u]+g.edges[u][i]
则修正dist[i]= dist[i]>dist[u]+g.edges[u][i]
path[i]=u;
}
}
1.从T中选取一个其距离值为最小的顶点W, 加入S
2.S中加入顶点w后,对T中顶点的距离值进行修改:
若加进W作中间顶点,从V0到Vj的距离值比不加W的路径要短,则修改此距离值;
3.重复上述步骤1,直到S中包含所有顶点,即S=V为止。
图像表示如下
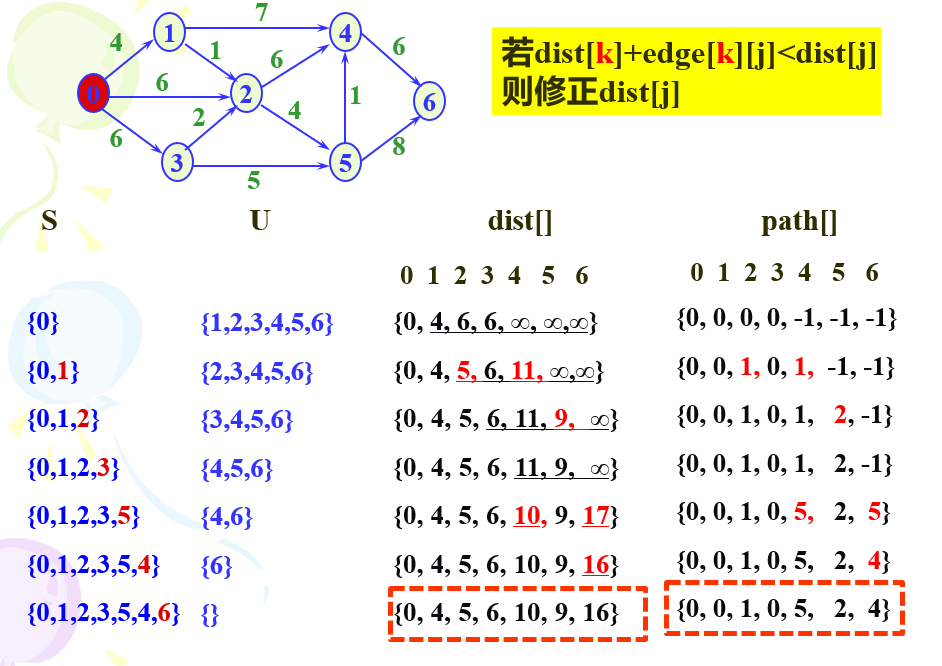
用佛洛依德(Floyd)算法求最短路径
void Floyd(Graph g)
{
建立A数组和path数组,A[MAXV][MAXV],path[MAXV][MAXV];
for i=0 to g.n;
for j=0 to g.n
{
A和path数组初始化;
}
for k=0 to g.n
for i=0 to g.n
for j=0 to g.n
if(A[i][j]>A[i][k]+A[k][j])//找到更短路径
{
修改路径长度;
path[i][j]=k;
}
}
拓扑排序、关键路径
拓扑排序:在一个有向图中找一个拓扑序列的过程称为拓扑排序。
1.从有向图中选取一个没有前驱的顶点,并输出之;
2.从有向图中删去此顶点以及所有以它为尾的弧;
3.重复上述两步,直至图空,或者图不空但找不到无前驱的顶点为止。
typedef struct
{
int data;
int count; //存放顶点入度
ArcNode* firstarc;
}VNode;
void TopSort(AdjGraph*G)
{
遍历邻接表
计算每个顶点的入度,存入头结点count成员
遍历图顶点
若发现入度为0顶点,入栈st
while(栈不空)
{
出栈节点v,访问。
遍历v的所有邻接点
{
所有邻接点的入度-1
若有邻接点入度为0,则入栈st
}
}
}
void topSort(AdjMGraph* G) //拓扑排序算法
{
int i,j;
int St[MAXV];
int top=-1;
ArcNode*p;
for(i=0;i<G.n;i++)
G->adjlist[i].count=0;
for(i=0;i<G.n;i++) //求顶点入度
{
p=G->adjlist[i].firstarc;
while(p!=NULL)
{
G->adjlist[p->adjvex]++;
p=p->nextarc;
}
}
for(i=0;i<G.n;i++) //将入度为0的进栈
if(G->adjlist[i].count==0)
{
top++;
St[top]=i;
}
while(top>-1)
{
i=St[top];
top--;
cout<<i;
p=G->adjlist[i].firstarc;
while(p!=NULL)
{
j=p->adjvex;
G->adjlist[j].count--;//出边邻接点的入度减1
if(G->adjlist[j].count==0)//减1后若入度为0进栈
{
top++;
St[top]=j;
}
p=p->nextarc;
}
}
}
关键路径
1.关键路径为原点到汇点的最长路径
2.ve为事件的最早开始时间,vl为事件的最迟开始时间
过程如下:
- 求拓扑序列
- 按拓扑序列求ve数组
- 按拓扑序列和ve数组求vl数组
- 计算边的最早和最迟时间,即e和l
- 找e=l边即为关键活动,边连起来即为关键路径
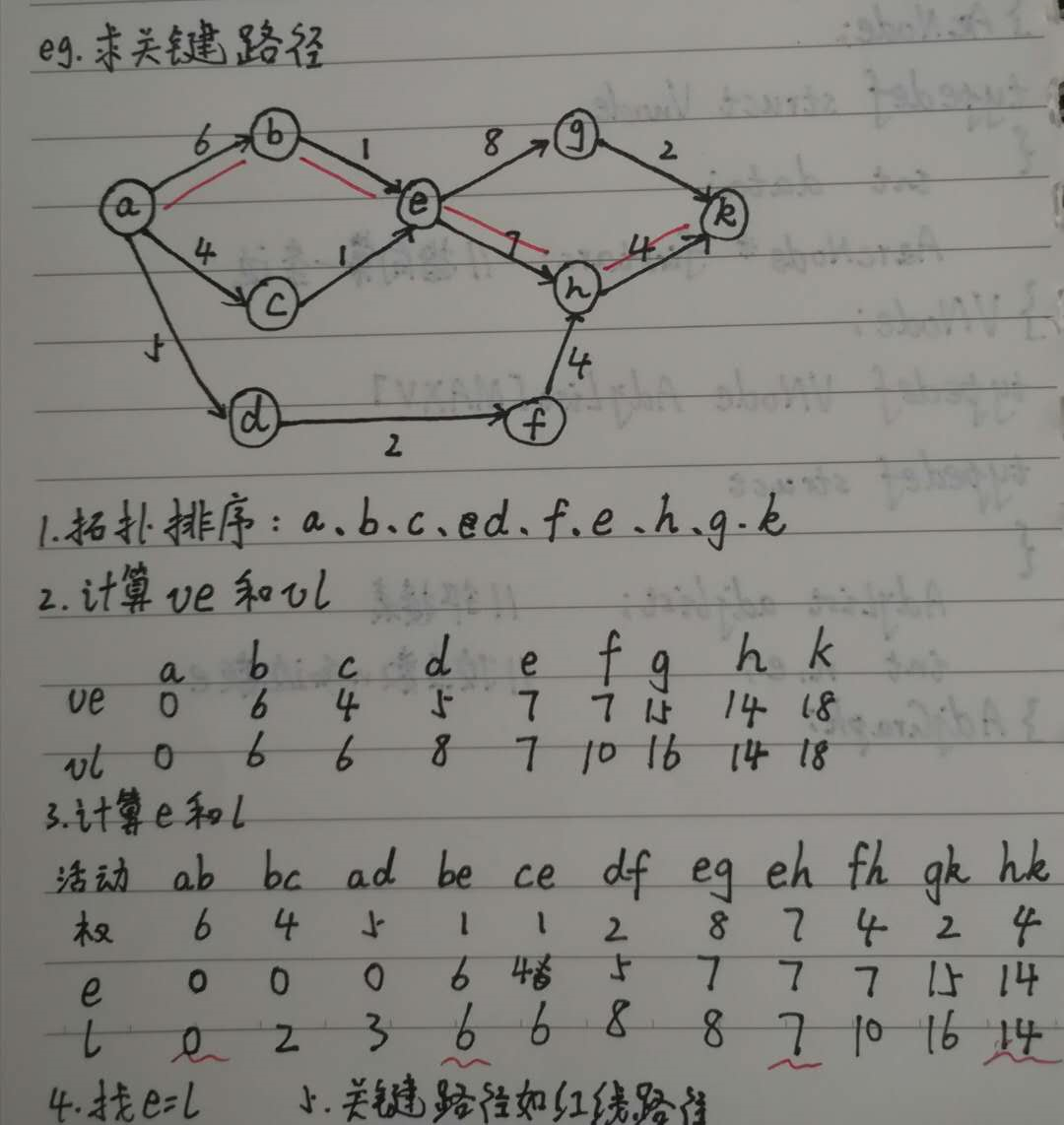
1.2.谈谈你对图的认识及学习体会。
- 图需要记住的专业术语比较多,如连通分量,图,有向图和无向图等
- 图的算法很多,而且难度也挺大的,代码量都比较大
- 图的存储结构也是目前学的最复杂的了,邻接表的存储结构需要多个结构体
- 感觉图的编程题比较更接近实际生活问题了,例如村村通和旅游规划,这类题目实际性强,比较有趣
- 图的代码比较难理解,需要在编程过程中理解,看是很难记住的
2.阅读代码
2.1 题目及解题代码


2.1.1 该题的设计思路
用二维数组dp来存储答案,利用小机器人只能往右或者往下,那么dp[i][j]的值就是第 i 行第 j 列这个格子的上面那
个格子的值加上左边那个格子的值,也就是dp[i][j] = dp[i-1][j] + dp[i][j-1],因为这两个格子都可以走到
dp[i][j]这个格子,那么他们的路径数之和就是dp[i][j]的值。
2.1.2 该题的伪代码

2.1.3 运行结果
运行结果与题目所给答案一致
2.1.4分析该题目解题优势及难点。
解题优势:利用数学规律和题目所给的机器人行走方式进行解题,利用当前的路径条数等于左边格子的路径加上边格子的路径
即dp[i][j] = dp[i-1][j] + dp[i][j-1],将复杂问题通过规律简化
难点:解题思路很难,因为如果直观地要求到达指定格子的路径条数是非常复杂的,格子越多越复杂,因此只能想办法找出规律
2.2 题目及解题代码
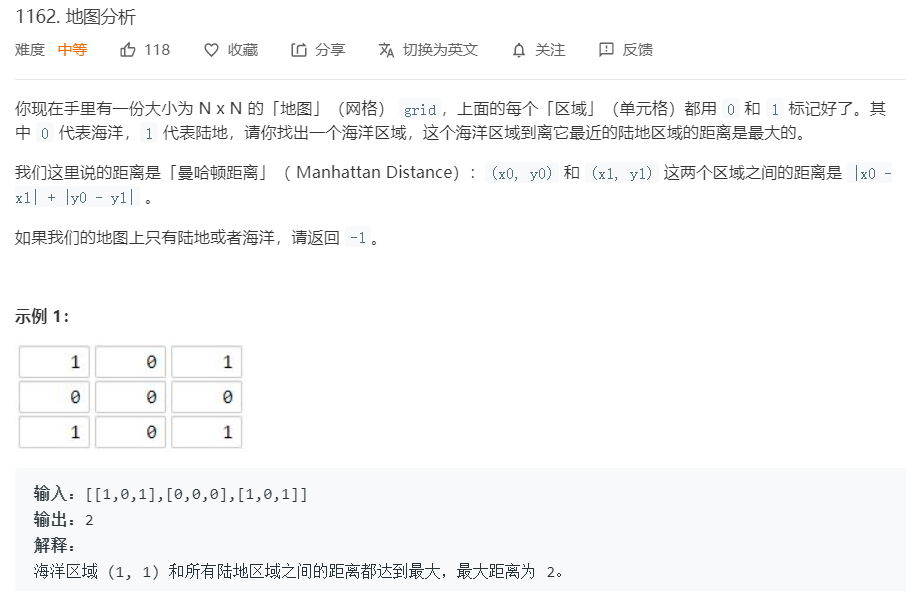

2.2.1 该题的设计思路
从每个小岛出发,周围的格子距离加1,最后到达的海域的距离即为所求

2.2.2 该题的伪代码

2.2.3 运行结果
2.2.4分析该题目解题优势及难点。
解题优势:思路比较好理解,运用队列来辅助搜索
难点:对于图的遍历要非常熟悉,要灵活运用广度搜索
2.3 题目及解题代码
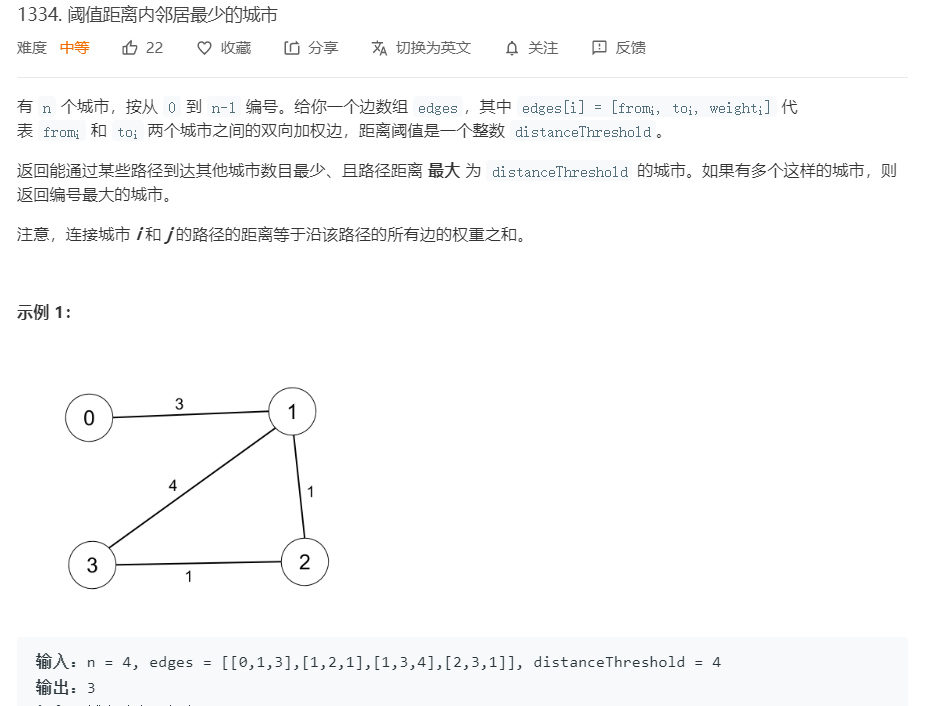


2.3.1 该题的设计思路
1.使用Floyd算法求出各个城市到其它城市的距离,保存在矩阵D[n][n]中。
2.遍历D[n][n],统计各个城市在距离不超过 distanceThreshold 的情况下,能到达的其它城市的数量。
3.返回能到达其它城市最少的城市
2.3.2 该题的伪代码

2.3.3 运行结果

2.3.4分析该题目解题优势及难点。
解题优势:运用Floyd算法求出最短路径来进行解题
难点:题目意思比较难懂,需要比较好的逻辑思维和对Floyd算法掌握的比较熟悉