在感知机一节中说到,我们在线性可分的情况下,寻找一个超平面使得
一部分实例$sum_{i=1}^{n}w _{i}cdot x_{i}>0$,
另一部分实例$sum_{i=1}^{n}w _{i}cdot x_{i}<0$
但是感知机的解不唯一,所以会出现这样的情况
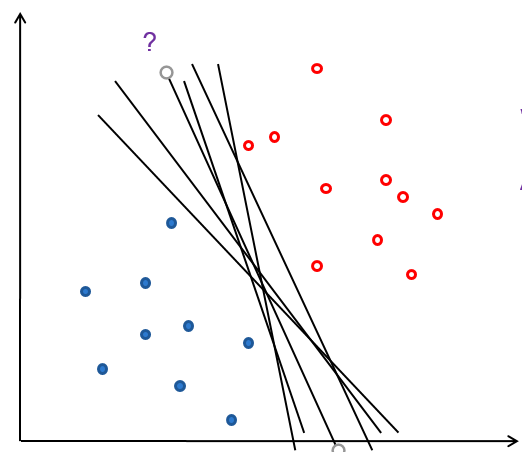
我们应该如何选择一个最佳的解呢?
首先定义几何间隔为:
$d=frac{yleft | wcdot x_{i}+b ight |}{left | w ight |_{2}}$
其实就是感知机损失函数在固定分子之前的形式
定义函数间隔为:
$y_{i}(wcdot x_{i}+b)$
几何间隔d才是真正的点到超平面的距离
支持向量
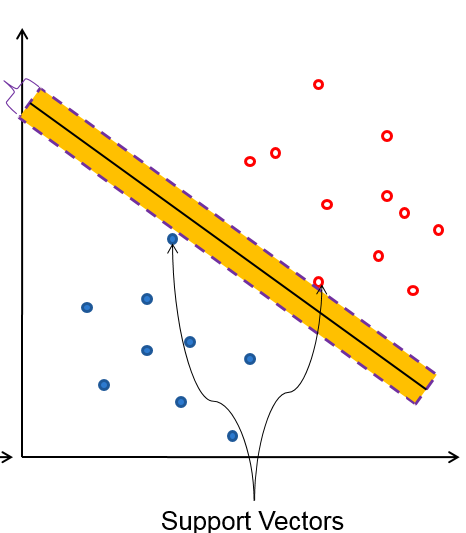
图中过样本点的虚线表示的就是支持向量(support vector)
中间的实线就是超平面$y_{i}(wcdot x_{i}+b)=0$
一般设置支持向量为 $y_{i}(wcdot x_{i}+b)=+1/-1$
SVM希望所有的点到超平面的距离都大于1,公示表示为
max $ d=frac{1}{left | w ight |_{2}}sum_{x_{i}subseteq M}^{ }y_{i}(wcdot x_{i}+b) $
并且 $s.t y_{i}(wcdot x_{i}+b)≥1$
与感知机不同,我们固定d的分子为1,
又最大化$frac{1}{left | w_{2} ight |_{2}}$,等同于最小化$frac{1}{2}left | w_{2} ight |_{2}^{2}$
tips
要加1/2 和 平方 单纯的为了求导的方便
所以优化公式变为:
min $frac{1}{2}left | w_{2} ight |_{2}^{2}$
$s.t y_{i}(wcdot x_{i}+b)≥1$
建立拉格朗日函数,将不等于约束变成无约束优化问题
$L(w,b,a)=frac{1}{2}left | w_{2} ight |_{2}^{2}-sum a_{i}left [ yleft ( wcdot x+b ight )-1 ight ]且a_{i}> 1 $
这里i= 1,2,,,m,即样本个数。下文为了编辑公式方便不再赘述。
(这里不明白的为什么ai≥0,请看KKT条件一文)
所以优化目标变成:
$underset{w,b}{min}$ $underset{ageq 0}{max}$ $L(w,b,a)$
这里为什么要max ai
博主个人认为 是要得到L(w,b,a)的最小值,但是关于a的那部分前面是负号,所以要求L最大时a的值。(ps:纯属个人意见,希望大家指点。)
欲得到min L(w,b,a)时对应的w,b,对L求偏导
$frac{partial L}{partial w}=0Rightarrow w = sum a_{i}y_{i}x_{i}$
$frac{partial L}{partial b}=0Rightarrow b = sum a_{i}y_{i}$
这里w可由a表示,带入方程,我们可要求出maxL时对应的 a便可求得w,b暂时先不管。
定义:$psi (alpha )=underset{w,b}{min} {w,b}$ $L(w,b,a)$
将$w = sum a_{i}y_{i}x_{i}$带入
得到

(公式太过庞大,编辑公式太繁琐,so..盗图)推导很关键,反正博主自己推不出来...
所以,优化目标变成:
$underset{a}{max}=-frac{1}{2}sum sum a_{i}a_{j}y_{i}y_{j}x_{i}cdot x_{j}+sum a_{i}$
$s.t sum a_{i}y_{i}=0$
$a_{i}≥0 $
也可以去掉负号,变成:
$underset{a}{max}=frac{1}{2}sum sum a_{i}a_{j}y_{i}y_{j}x_{i}cdot x_{j}-sum a_{i}$
$s.t sum a_{i}y_{i}=0$
$a_{i}≥0 $
上述优化目标只有α未知,求得α即可得到w
α的计算使用SMO算法。假设得到α*
根据$w = sum a_{i}y_{i}x_{i}$,求得
$w* = sum a*_{i}y_{i}x_{i}$
求b
在线性可分的情况下,找到一个支持向量,必有$y_{s}(wcdot x_{s}+b)=1Rightarrow y_{s}(sum a*_{i}y_{i}x_{i}cdot x_{s}+b)=1$,可以求得b
![]()
线性不可分问题请看下一节soft margin(软间隔)。
给一个简单的小例子感受一下计算过程。
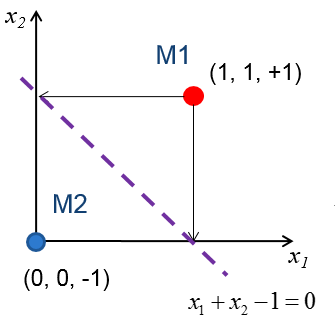
如图,两个样本M1,M2,每个样本两个特征X1,X2,一个Y(所以是三个点表示他的坐标)
求最佳线性分割平面
首先,根据最终的优化目标,其中第一个约束条件为$s.t sum a_{i}y_{i}=0$,可以得到
![]()
第二,根据$frac{1}{2}sum sum a_{i}a_{j}y_{i}y_{j}x_{i}cdot x_{j}-sum a_{i}$
为了计算简便,定义:$H = y_{i}y_{j}x_{i}cdot x_{j}$
所以

而

将H和第一步得到的$alpha _{1}=alpha _{2}$带入LD,有

现在欲得到优化目标最大对应的α,很明显,这是个开口向上的抛物线
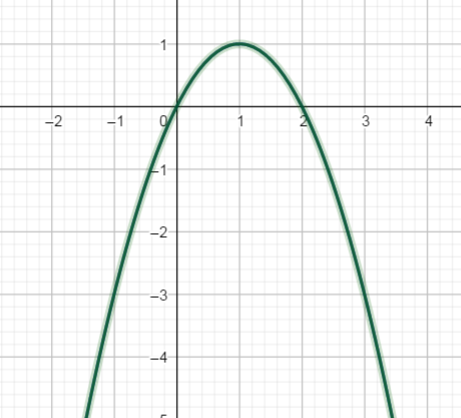
α取到1,优化目标值最大,所以
![]()
第三,w的求解。将α值带入$w = sum a_{i}y_{i}x_{i}$,得到
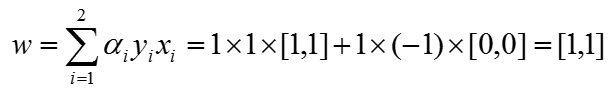
第四,b的求解。
因为只有两个样本,所以这两个点都在支持向量上,选M1带入w·x1+b=1有
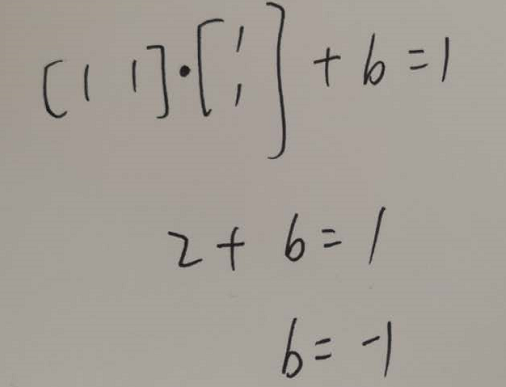
得到超平面
![]()
自我总结
(感知机与SVM的不同,感知机欲使误分类点到超平面的距离最小,SVM想让所有点到超平面的距离最大)