树状数组用于求区间和问题
这个数据结构比较简单,但是可能做题的时候都想不到竟然可以用树状数组可以做
解决的基本年问题o(lgn):
1:快速的求前缀和
2:修改某一个数
原理:
基于二进制。
x=2^i[k]+2^i[k-1]+...2^i[1]
那么便可以将前x个数分为以下几个区间
1:(x-2^i[1],x]
2:(x-2^i[1]-2^i[2],x-2^i[1]]
.....
(0,x-2^i[1]-...-2^i[k]]
区间都是左开右闭,区间(l,R]的长度一定是R的二进制表示的最后一位1所对应的次幂,所以为[R-lowbit(R)+1,R]
其中lowbit(x)=x&(-x)表示x最后一位1所对应的次幂
在1~n中只有N个区间,因为每个区间由右端点来确定
需要一个数组c[x]=a[x-lowbit(x)+1,x]的和
c[1]=a[1]
c[2]=a[1]+a[2]
c[3]=a[3]
c[4]=a[1]+a[2]+a[3]+a[4]
c[5]=a[5]
c[6]=a[5]+a[6]
c[7]=a[7]
c[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]
c[9]=a[9]
c[10]=a[9]+a[10]
c[11]=a[11]
c[12]=a[9]+a[10]+a[11]+a[12]
c[13]=a[13]
c[14]=a[13]+a[14]
c[15]=a[15]
c[16]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]+a[9]+a[10]+a[11]+a[12]+a[13]+a[14]+a[15]+a[16]
c[x]存储的是以x结尾的长度为x最后一位1对应的次幂
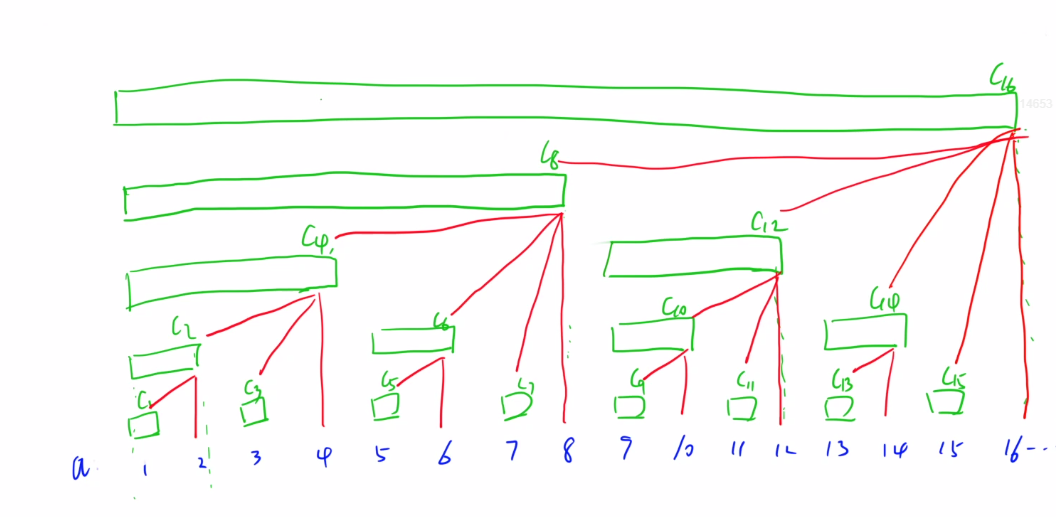
树状数组主要包含两个部分
1:求前缀和
2:修改一个值,更改其所有的父亲节点
#define lowbit(x) (x&-(x)) //求出x的最后一位1对应的次幂值 void add(int x,int d){//修改某一额值a[x]加上d while(x<=n){ c[x]+=d; x+=lowbit(x); } } int sum(int x){//求前缀和 int sum=0; while(x>0){ sum+=c[x]; x-=lowbit(x); } return sum; }
但是这里需要注意的是lowbit()是利用负数的补码表示,所以数组的下标一定要从1开始
初始化问题:给你一个数组a,建立他的树状数组
1:最简单的方法就是遍历每个元素a,那么复杂度是O(nlgn) for(int i=1;i<=n;i++) add(i,a[i]);
2:可以根据定义出发,可以达到O(n),先创建一个a的前缀和数组s,那么c[x]=s[x]-s[x-lowbit(x)];
最简单的树状数组是只对某一个点进行修改,而树状数组的扩展可以完成给某一段区间进行加,求某一个点的值
其实利用的是差分的思想。
差分就是在原序列a的基础上,进行操作,可以让a从1开始,并且a[0]=0,那么差分数组b[i]=a[i]-a[i-1],其中b[0]=a[0]=0.
那么给区间[l,r]都加上d就是让b[l]+=d,b[r+1]-=d,就变成的最简单的树状数组的单点修改。而查询某一个a[x],就是求b的前x项的和,也就是转换为了最简单的树状数组的前缀和
树状数组的进一步扩展:区间加和区间求和
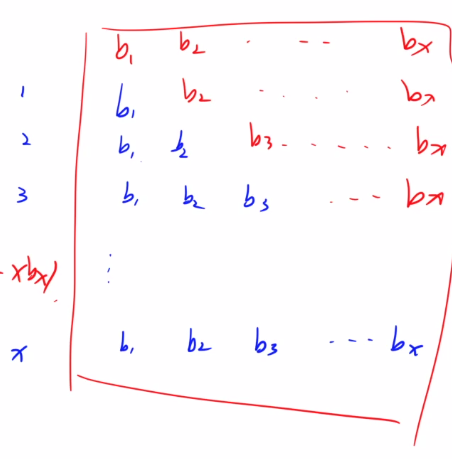
这张图片中的蓝色的,每一行蓝色的和都是一个元素a,分别表示a[1].....a[x].所以我们只需要求出a的前缀和,那么对于区间的和就显而易见了。至于图中的红色是一个填补的作用,我们可以知道a的前缀和就是蓝色+红色再减去红色。首先,蓝色+红色=a[x]*(x+1),而a[x]可以由差分数组b的前缀和求出。红色其实是i*b[i]的前缀和。所以a的前x的和S[x]=b[i]的前缀和*(x+1)-i*b[i]的前缀和。所以查询[l,r]=S[r]-S[l-1]