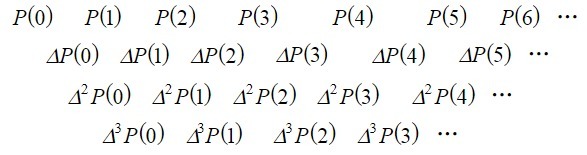对插值法及拉格朗日插值多项式的初步理解运用
(Interpolation)
"插值",适用于解决复杂、难于计算的函数表达式问题的有力手段,更有时根本没有具体的函数,只有对应采样点的几个函数值,而要求计算非采样点的函数值的问题,此时插值法就可以构造出该函数的近似表达式来解决问题。
一:什么是插值
插值是属于数学数值分析领域的内容,常被称作内插或者__插值__。接下来给出定义:
给定N个数据离散点((x_k,y_k)),其中(k = 1,2,3...N)。对于(x)求(x)对应的(y)值叫做内插。
定义域在区间([A,B])上有意函数(F),已知函数(G)在([A,B])范围内满足(G(x_i) = F(x_i) = 1,2...N)
则称(G(x))为(F(x))关于节点({x_i}_{i = 0}^N)上的插值函数。
假设我们已经求得(x_i)集合中的最大值(MAX)和最小值(MIN)
用插值函数(G(x))计算被插值函数(F(x))在点(x in (MIN, MAX))处的近似值的方法称为内插法。
用插值函数(G(x))计算被插值函数(F(x))在点(x in [A, B])但(x otin [MIN, MAX])处的近似值的方法称为外插法。
那么你现在已经基本了解了什么是插值,下面我们来看一些关于插值方法的东西。
二:插值方法简介
1.片段插值
这种插值方法几乎不能算是插值了,所实话如果没有维基百科编者根本就不知道有这种插值方法以及这样也能算是插值。
简单来说就是找到离(x)最近的采样点(x_i),然后将(y)值分配为(y_i)。因此它的别称就是__最近邻插值__。但是就和wiki说的一样,这种插值方法是几乎碰不到的,因为出不了什么很高深的符合当前阶段学习的题目,但同时如果可以使用这种方法,无疑将使时间和复杂性都大大降低。
2.线性插值
这种插值从某种意义上说是利用了斜率,但实际上就是很简单的取平均值而已。
假设我们已知了所有自然数采样点({x_i}),而我们要求的插值点是(x_{i+0.5}),那么发现当前插值点是处于(x_i和x_{i+1})之间,那么我们取的分配值就是(frac{y_i+y_{i + 1}}{2})。以数学公式的方法表达就是:
(y = y_a + (y_b - y_a) frac{x - x_a}{x_b - x_a})
(G(x) = y_a frac{x - x_b}{x_a - x_b} + y_b frac{x - x_a}{x_b - x_a})
发现(G(x))实际上是两个一次多项式的组合。也就是说,我们过这两个点分别作一次多项式(l_a = frac{x - x_b}{x_a - x_b},~l_2 = frac{x - x_a}{x_b - x_a}),那么(G(x) = y_al_a + y_bl_b)。
而实际上上述两种插值方法都存在误差,撇开片段插值不谈,线性插值的误差来源只要是因为插值点(x_k)是不可微分的,而计算得出的误差是(|F(x) - G(x)| leq C(x_b - x_a)^2~where~C= frac18max_{r in[x_a, x_b]}|g^{''}(r)|)
其与数据点的距离平方成正比。
我们发现前两者的不同在于第一个找到了一个采样点进行插值,而线性插值则找到了两个点,因为两点确定一个一次函数。相同的,我们也有三点确定的二次函数的抛物线插值法,这里不再进行分析。
3.多项式插值
已知函数(F(x))在([A, B])上(N + 1)个点处的函数值({y_i}_{i = 0}^N),求次数不超过(N)的多项式(G(x) = c_0 +c_1x+...+c_Nx^N)使得(G(x) = F(x))称为多项式插值。
定理:多项式插值函数存在且唯一:我们都知道过(N + 1)个点做一个(N)次函数最多只能做一个,而做一个(≥N)次的函数却可以有无数个。
三:拉格朗日插值法
建立插值多项式的方法(简称为插值法)最基本的是需要求解线性方程组,而这是最为冗杂,最为复杂的算法,一般没有特殊情况是不会用这种方法构造插值多项式的。因此经过前人的努力,引入了一种更为简单,实现更为便捷的插值法:拉格朗日插值法。与之相通的有牛顿插值法,而我们又知道多项式插值函数的唯一性,因此恒有(L_n(x) = N_n(x))。(L:拉格朗日,N:牛顿)。
在准备好了解拉格朗日插值法之前,我们先引入一个基函数的概念。
记(H_n(x))为次数不超过(N)的多项式全集,也就是有(H_0(x),H_1(x)...H_n(x)),设其构成(H_n(x))的一组基,则插值多项式可表示为(G(x) = a_0H_0(x) + ... + a_nH_n(x))。
那么我们只要寻找到合适的基函数和插值多项式在这组基下的线性表示系数,就可以通过基函数构造插值多项式,也就是__基函数插值法__。
回到拉格朗日插值上来,我们首先寻找基函数。
设(l_k(x))是(n)次多项式,在节点(x_0,x_1...x_n)上满足(l_k(x_i) = 1 ~(i = k))或(l_k(x_i) = 0~(i ≠ k)),则称(l_k(x))为节点({x_i}_{i = 0}^N)上的(n)次拉格朗日插值基函数。
构造法可以知道(l_k(x) = prod_{i = 0,i ≠ k}^{N} frac{x - x_i}{x_k - x_i})
知道基函数之后我们用基函数求(G(x) = a_0l_0(x) + ... + a_nl_n(x)),带入(G(x_i) = y_i)可得
(L_n(x) = sum_{k = 0}^ny_kl_k(x))
上方的(L_n(x))就是我们的拉格朗日插值多项式,具有结构清晰紧凑的特点,是用于理论分析的一般手法。根据插值误差估计定理可以估计出误差为:(frac{y_{n + 1}(ζ)}{(n + 1) !} omega_{n+1}(x)),其小于(frac{M_{n+1}}{(n+1)!}|omega_{n+1}|(x))。
重心拉格朗日插值法
按照维基百科说的,这是对拉格朗日插值法的一种改进。当然,指的是速度上的,误差方面并没有什么差别。
按照均摊来说,如果用朴素拉格朗日插值法求插值函数,时间复杂度是(O(N^2)),而中心拉格朗日插值法可以将时间复杂度压缩到(O(N))。讲了整整一个量级,不可谓不改进。但从大多数方面来说,朴素拉格朗日也足足够用了。
实质上一致的前提下,中心拉格朗日插值法改写了拉格朗日基本多项式(l_j(x))。
(l(x) = prod_{i = 0}^K(X - X_K)),使(l_j(x) = frac{l(x)}{x - x_j} imes frac{1}{prod _{i = 0}^K(x_j - x_i)})
然后定义一个重心权(w_j = prod_{i = 0}^Kfrac{1}{x_j - x_i}),则(L(x) = l(x)sum_{j = 0}^K frac{w_j imes y_j}{x - x_j})。
然后这个玩意怎么改进拉格朗日了呢?
当插值点的个数增加一个的时候,将每一个(w_j)都除以)((x_j - x_{K + 1})),得到(w_{k + 1}),直接省掉了一个循环,因此复杂度变为了(O(N))。
(维基百科原话,还是能看懂的。)
据说这个重心拉格朗日插值法不仅仅速度更优,并且省掉了多项式(l(x))的计算,还有说什么不同于第一型的拉格朗日插值函数的向后稳定,这个改进后的第二型拉格朗日插值函数是向前稳定的,勒贝格常数非常小,因为什么切比雪夫节点插值的极佳稳定性之类的。
当然,这种切比雪夫节点、勒贝格常数之类的就不是我们此次要学习的范围了,读者只要重心拉格朗日插值法把朴素拉格朗日插值法速度上甩了一大截就可以了。追求完美的读者可以试着一学。
拉格朗日插值基函数的性质及其应用
- 当(F(x))为一个多项式且次数(leq n)时,有(F^{(n+1)}(x) equiv 0),所以(R_n(x) = F(x) - L_n(X) equiv 0),(R为误差)因此(n)次插值多项式对于次数(leq n)的多项式是精确的。
- 若(F(x) = x^k)其中(k leq n),那么(R_n(x) = x^k - sum_{j = 0}^nX^kl_j(x) = 0)。特别的,当(k = 0)的时候有(sum_{j = 0}^nl_j(x) = 1)。
结合上面的性质及其公式,我们尝试解决一些实际问题。从最经典的应用开始,熟练地运用拉格朗日公式解决插值类问题。
连续自然数幂和(差分表)
已知(K),求(sum _{i = 1}^Ni^K)
首先介绍一个叫做“差分表”的小知识点。这个名字我们很自然想到差分的思想,而我们平常用的差分((a[i + 1] - a[i]))只是叫做__一阶差分__,根据这个最基本的,我们定义出"差分表"的东西。
对于函数(F(x)),把(F'(X) = F(X + 1) - F(X))叫做一阶差分,称(F'(X))叫做差分算子。引申出对于(K > 1),有(F'^K(X) = F'^{K - 1}(X + 1) - F'^{K - 1}(X))为(K)阶差分。
算出所有的(F'^K(X)),将(X = 1,2,3...H),代入每一个(F'^K(X)),得到一个二维的表。即是差分表。
可以观察到列数递减,我们把所有的数插空排列,便形成了差分表的基本形状。
接着是引入的两个定理,可以直接使用:
如果多项式的次数为(N),则对于所有大于(N)的(K),多项式的(K)阶差分都恒等于(0)。
假设多项式(F(X))的差分表的左斜列中各个元素依次是(D_0,D_1...D_M),那么对于这个多项式的和恒有:
(Sum(X) = sum_{X = 0}^NF(X) = D_0C_{N + 1}^1 + D_1C_{N + 2}^1 + H + D_MC_{N + 1}^{M + 1})
以这个差分表作为工具,我们尝试从简单开始逐步解决这个问题。
首先假设(F(X) = X),那么 我们构造出差分表的样子大概是这样的:
0 1 2 3 4 5 6 ……
1 1 1 1 1 1 ……
0 0 0 0 0 ……
所以(Ans = 1 + 2 + H + N = 0 imes C_{N + 1}^1 + 1 imes C_{N + 2}^2)
所以(Ans = frac{N(N + 1)}{2})
接着引申到(F(X) = X^2),建立出差分表
0^2 1^2 2^2 3^2 4^2 5^2 6^2 ……
1 3 5 7 9 11 ……
2 2 2 2 2 ……
0 0 0 0 ……
答案就是(1^2 + 2^2 + H + N^2 = 0C_{N + 1}^1 + 1C_{N + 2}^1 + H + 2C_{N + 1}^{M + 1})
所以答案为(frac{N(N + 1)(2N + 1)}{6})
因此我们引出了(Ans(K))就是一个关于(N)的(K + 1)次多项式。
知道如此结论,我们就可以选择(K + 1)个点然后利用拉格朗日插值公式进行计算了。夫再度(O(K))。
例题:Study
给定了(K, A, N, D),求(sum_{i = 0}^N sum_{j = 1}^{A + iD} sum_{l = 1}^jl^K)
实际上和上面那个题没有什么很大的区别,式子虽然很长,我们从里到外分开考虑即可
最里面的(sum_{l=1}^jl^k)是一个关于(j)的(k+1)次的多项式。把其差分表的第一条对角线求出来。
然后(sum_{j=1}^{A+iD}sum_{l=1}^jl^k)是关于(i)的(k+2)次的多项式。(O(k^2))求出(i=0,1,...k+2)的值。
所以答案就是一个关于(N)的(k+3)次的多项式。求其第一条对角线即可。
拉格朗日插值法的代码实现
经过上述的学习之后,代码实现可能反而是小事了。给出模板题的连接:拉格朗日插值法
给出(N)个点((X_i,Y_i)),确定一个唯一的(N - 1)次多项式,代入(k)求值。
代入所有的点,按照上述的讲解,爆搞就可以了。
inline long long QuickPow(LL X, LL Y) {
long long Ans = 1 ; while (Y) {
if (Y & 1) Ans = Ans * X % Mod ;
Y >>= 1 ; X = X * X % Mod ;
} return Ans ;
}
int main() {
N = Read() ; K = Read() ;
for (int i = 1 ; i <= N ; i ++) X[i] = Read(), Y[i] = Read() ;
for (int i = 1 ; i <= N ; i ++) {
int Ken = 1 ;
for (int j = 1 ; j <= N ; j ++) {
if (i == j) continue ;
Ken = Ken * (X[i] - X[j] + Mod) % Mod ;
} Ken = QuickPow(Ken, Mod - 2) ;
for(int j = 1 ; j <= N ; j ++) {
if (i == j) continue ;
Ken = Ken * (K - X[j] + Mod) % Mod ;
} Ken = Ken * Y[i] % Mod ;
Ans = Ans + Ken % Mod ;
} printf("%lld", Ans % Mod) ; return 0 ;
}
后记
都是说拉格朗日插值法好用,之后才知道它的优点在哪:
代替线性,抛物线之类的插值方法繁琐的公式结构和计算方法,其公式结构整齐紧凑,好看得多。
可能有人感觉很好笑,但是这确实是很重要的一点。考场上推出来超级复杂繁琐的方程式会让你心态爆炸的,因此简单整齐的公式结构也是十分重要的,好写好看,这可能也是他广为人用的原因之一吧。
但当然,数学仍然是不完整的,对于采样点较多的情况时出现的龙格现象,也表明拉格朗日插值法具有数值不稳定的特点,因此大多数情况,拉格朗日插值法仍用于解决次数较低的插值多项式问题。
牛顿插值法不再将了,因为其本质是一样的,充其量走了不同的路子而已,想学的朋友可以去了解一下。