图的基本概念:
点用边连起来就叫做图,实际上:图是一种数据结构,定义为:graph=(V,E)。V是一个非空有限集合,代表顶点(结点),E代表边的集合。
图分为有向图与无向图两种:
有向图:图的边有方向,只能按箭头方向从一点到另一点。
无向图:图的边没有方向,可以双向。
结点的度:无向图中与结点相连的边的数目,称为结点的度。
结点的入度:在有向图中,以这个结点为终点的有向边的数目。
结点的出度:在有向图中,以这个结点为起点的有向边的数目。
权值:边的“费用”,可以形象地理解为边的长度。
连通:如果图中结点U,V之间存在一条从U通过若干条边、点到达V的通路,则称U、V 是连通的。
回路:起点和终点相同的路径,称为回路,或“环”。
完全图:一个n 阶的完全无向图含有n*(n-1)/2 条边;一个n 阶的完全有向图含有n*(n-1)条边;
稠密图:一个边数接近完全图的图。
稀疏图:一个边数远远少于完全图的图。
强连通分量:有向图中任意两点都连通的最大子图,特殊地,单个点也算一个强连通分量。
图的遍历:
深度优先与广度优先遍历:
从图中某一顶点出发系统地访问图中所有顶点,使每个顶点恰好被访问一次,这种运算操作被称为图的遍历。
图的遍历分为深度优先遍历和广度优先遍历两种方法,两者的时间效率都是O(n*n)。
当我们进行深搜时:
void dfs(int i) //图用数组模拟邻接表存储,访问点i
{
visited[i] = true; //标记为已经访问过
for (int j = 1; j <= num[i]; j++) //遍历与i相关联的所有未访问过的顶点
if (!visited[g[i][j]])
dfs(g[i][j]);
}
int main()
{
……
memset(visited,false,sizeof(visited));
for (int i = 1; i <= n; i++) //每一个点都作为起点尝试访问,因为不是从任何
//一点开始都能遍历整个图的,例如下面的两个图。
if (!visited[i])
dfs(i);
……
return 0;
}
广度优先遍历:
广度优先遍历相对深度优先来说比较复杂,但是与广搜BFS相似,修改一下BFS就容易改成广度优先遍历。
最短路径算法
在求最短路径这里,有以下几种方法:
一、Floyed(弗洛伊德)算法:这是最简单的最短路径算法,可以计算图中任意两点间的最短路径。
但是由于是挨个查找,复杂度相对较高,是O (N3)。不过弗洛伊德算法也适用于出现负边权的情况。
大体代码如下:
For (k = 1; k <= n; k++)
For (i = 1; i <= n; i++)
For (j = 1; j <= n; j++)
If (dis[i][j] >dis[i][k] + dis[k][j])
dis[i][j] = dis[i][k] + dis[k][j];
其中dis[i][j]得出的就是从i到j的最短路径。
当然在进行操作之前,首先要进行初始化,点u、v如果有边相连,则dis[u][v]=w[u][v]。如果不相连则dis[u][v]=0x7fffffff设为最大值(不相连则权值最大)
二、Dijkstra算法:用来计算从一个点到其他所有点的最短路径的算法,是一种单源最短路径算法。也就是说,只能计算起点只有一个的情况。相对于弗洛伊德算法来说,总的查找力降低,而且不可处理负边权的情况,但是在对某个点的查找中效率大大提升,算法效率为O (N2)
三、Bellman-Ford算法:简称Ford(福特)算法,同样是用来计算从一个点到其他所有点的最短路径的算法,也是一种单源最短路径算法。能够处理存在负边权的情况,但无法处理存在负权回路的情况。算法时间复杂度为:O(NE),其中N是顶点数,E是边数。
虽然Bellman-Ford算法可以求出存在负边权情况下的最短路径,却无法解决存在负权回路的情况。
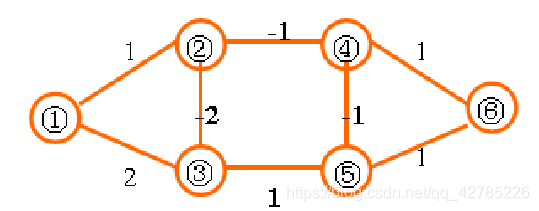
我们根据以上图片:负权回路是指边权之和为负数的一条回路,上图中②-④-⑤-③-②这条回路的边权之和为-3。在有负权回路的情况下,从1到6的最短路径是无穷小,因为我们可以绕这条负权回路走无数圈,每走一圈路径值就减去3,最终达到无穷小。
所以说存在负权回路的图无法求出最短路径,Bellman-Ford算法可以在有负权回路的情况下输出错误提示。
如果在Bellman-Ford算法的两重循环完成后,还是存在某条边使得:dis[u]+w<dis[v],则存在负权回路:
For每条边(u,v)
If (dis[u]+w<dis[v]) return False
如果我们规定每条边只能走一次,在这个前提下可以求出负权回路的最短路径。
图论这里概念相对较多,算法的实现方式也比较多,相对来说也比较难,还要慢慢琢磨。