A - Courses
题意
有(N)位学生与(P)门不同的课程,第(i)门课程有(Count_i)名学生想要修读
每位学生只能够选择一门课进行修读,每门课也只能有一位学生进行修读
试判断是否存在一种学生的分配方案,使得每门课都能够有一位学生修读
标签
二分图最大匹配
思路
二分图最大匹配 - 匈牙利算法模板题
来源
Southeastern Europe 2000
代码一(vis标记是否已被搜索过)
#include<bits/stdc++.h>
using namespace std;
/*
* N表示学生数量
* P表示课程数量
* G[i]存储课程i可选择的所有学生
* match[j]存储学生j当前匹配的课程编号,未选择则置0
* vis[j]标记当次搜索过程中学生j是否已被搜索过
*/
int N,P;
vector<int> G[105];
int match[305];
bool vis[305];
bool hungary(int u)
{
// 遍历所有课程u可选择的学生v
for(int v:G[u])
{
// vis数组防止在某次搜索中走重边,导致死循环
if(!vis[v])
{
vis[v]=true;
// 如果学生v未被选择,或者可以改变他的选择
if(!match[v]||hungary(match[v]))
{
match[v]=u;
return true;
}
}
}
return false;
}
void solve()
{
scanf("%d%d",&P,&N);
memset(match,0,sizeof match);
for(int i=1;i<=P;i++)
G[i].clear();
for(int i=1;i<=P;i++)
{
int C,S;
scanf("%d",&C);
while(C--)
{
scanf("%d",&S);
G[i].push_back(S);
}
}
// 遍历所有课程,尝试匹配
for(int i=1;i<=P;i++)
{
memset(vis,false,sizeof vis);
if(!hungary(i))
{
puts("NO");
return;
}
}
puts("YES");
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
solve();
return 0;
}
代码二(vis描述某次搜索的源编号/当次是否已被搜索过)
#include<bits/stdc++.h>
using namespace std;
/*
* N表示学生数量
* P表示课程数量
* G[i]存储课程i可选择的所有学生
* match[j]存储学生j当前匹配的课程编号,未选择则置0
* vis[j]表示上一次搜索学生j时的源课程编号
*/
int N,P;
vector<int> G[105];
int match[305];
int vis[305];
bool hungary(int u,int t)
{
// 遍历所有课程u可选择的学生v
for(int v:G[u])
{
// vis防止在某次搜索中走重边,导致死循环
if(vis[v]!=t)
{
vis[v]=t;
// 如果学生v未被选择,或者可以改变他的选择
if(!match[v]||hungary(match[v],t))
{
match[v]=u;
return true;
}
}
}
return false;
}
void solve()
{
scanf("%d%d",&P,&N);
memset(match,0,sizeof match);
memset(vis,0,sizeof vis);
for(int i=1;i<=P;i++)
G[i].clear();
for(int i=1;i<=P;i++)
{
int C,S;
scanf("%d",&C);
while(C--)
{
scanf("%d",&S);
G[i].push_back(S);
}
}
// 遍历所有课程,尝试匹配
for(int i=1;i<=P;i++)
{
//不需要每次重置vis,每次多传一个参数限制
if(!hungary(i,i))
{
puts("NO");
return;
}
}
puts("YES");
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
solve();
return 0;
}
B - Strategic Game
题意
给定一张树图,你可以往图中的节点上放士兵
每个士兵可以观察与其所在节点相邻的所有边
问最少需要放多少士兵,使得整张图所有边都能被观察到
标签
最小顶点数覆盖
思路
换言之,也就是选择最少的顶点数,使得所有边连接的两个点中都至少有一个点被选择到
即最大顶点数覆盖,答案等同于二分图最大匹配数
做法一是先染色再根据相同集合建边
做法二是建立双向边,等同于整张图被建立了两层,所有边连接不同层,每个顶点会被匹配两次,所以二分图匹配得到的答案会是正确答案的两倍
来源
Southeastern Europe 2000
代码
#include<bits/stdc++.h>
using namespace std;
vector<int> G[1505];
int match[1505],vis[1505];
bool hungary(int u,int t)
{
for(int v:G[u])
{
if(vis[v]!=t)
{
vis[v]=t;
if(!match[v]||hungary(match[v],t))
{
match[v]=u;
return true;
}
}
}
return false;
}
int main()
{
int n;
while(scanf("%d",&n)!=EOF)
{
memset(match,0,sizeof match);
memset(vis,0,sizeof vis);
for(int i=1;i<=n;i++)
G[i].clear();
for(int i=1;i<=n;i++)
{
int u,v,t;
scanf("%d:(%d)",&u,&t);
u++;
while(t--)
{
scanf("%d",&v);
v++;
// 建立双向边
G[u].push_back(v);
G[v].push_back(u);
}
}
int ans=0;
for(int i=1;i<=n;i++)
if(hungary(i,i))
ans++;
// 得到的答案是标准答案的两倍
printf("%d
",ans/2);
}
return 0;
}
C - Air Raid
题意
由(n)个点和(m)条有向边构成一张DAG图
现在要在某些点上放一些伞兵,让伞兵沿着图一直走,直到不能走为止
每条边只能由一个伞兵走过,问最少放多少个伞兵能够走完所有边
标签
最小路径覆盖
思路
有向无环图的最小路径覆盖 = 顶点数 - 最大匹配数
来源
Asia 2002, Dhaka (Bengal)
代码
#include<bits/stdc++.h>
using namespace std;
vector<int> G[125];
int match[125],vis[125];
bool hungary(int u,int t)
{
for(int v:G[u])
{
if(vis[v]!=t)
{
vis[v]=t;
if(!match[v]||hungary(match[v],t))
{
match[v]=u;
return true;
}
}
}
return false;
}
void solve()
{
int n,m;
scanf("%d%d",&n,&m);
memset(match,0,sizeof match);
memset(vis,0,sizeof vis);
for(int i=1;i<=n;i++)
G[i].clear();
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
G[u].push_back(v);
}
int r=0;
for(int i=1;i<=n;i++)
if(hungary(i,i))
r++;
printf("%d
",n-r);
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
solve();
return 0;
}
D - 奔小康赚大钱
题意
村长要为(n)位百姓分配(n)间房子,第(i)位百姓对第(j)间房子的出价是(c_{i,j})
问最终最大的收益总和
标签
二分图最大权完美匹配
思路
KM模板题,保证一定能够匹配且两集合点数均为(n),直接跑板子即可
来源
HDOJ 2008 Summer Exercise(4)- Buffet Dinner
代码一 DFS (O(n^4))
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int N=305;
int n,m,match[N];
bool vis1[N],vis2[N];
int favor[N][N];
int val1[N],val2[N],slack[N];
bool dfs(int p)
{
vis1[p]=true;
for(int i=1;i<=m;i++)
if(!vis2[i])
{
// p->i是条相等边,表示可以使用
if(val1[p]+val2[i]==favor[p][i])
{
vis2[i]=true;
if(!match[i]||dfs(match[i]))
{
match[i]=p;
return true;
}
}
// 否则更新松弛量
else
slack[i]=min(slack[i],val1[p]+val2[i]-favor[p][i]);
}
return false;
}
int KM()
{
for(int i=1;i<=n;i++)
{
// val1[i] 初始值设定为与左部点i相邻的边权最大值
val1[i]=-INF;
for(int j=1;j<=m;j++)
val1[i]=max(val1[i],favor[i][j]);
}
memset(match,0,sizeof match);
memset(val2,0,sizeof val2);
for(int i=1;i<=n;i++)
{
memset(slack,INF,sizeof slack);
//在无法匹配时,一直松弛下去
while(true)
{
memset(vis1,false,sizeof vis1);
memset(vis2,false,sizeof vis2);
if(dfs(i))
break;
// 求出所有当次搜索涉及到的点的slack的最小值
int d=INF;
for(int j=1;j<=m;j++)
if(!vis2[j])
d=min(d,slack[j]);
// 按最小值进行松弛
for(int j=1;j<=n;j++)
if(vis1[j])
val1[j]-=d;
for(int j=1;j<=m;j++)
if(vis2[j])
val2[j]+=d;
}
}
int res=0;
for(int i=1;i<=m;i++)
if(match[i])
res+=favor[match[i]][i];
return res;
}
int main()
{
while(scanf("%d",&n)!=EOF)
{
m=n;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&favor[i][j]);
printf("%d
",KM());
}
return 0;
}
代码二 BFS (O(n^3))
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int N=305;
int n,m,match[N],pre[N];
bool vis[N];
int favor[N][N];
int val1[N],val2[N],slack[N];
void bfs(int p)
{
memset(pre,0,sizeof pre);
memset(slack,INF,sizeof slack);
match[0]=p;
int x=0,nex=0;
do{
vis[x]=true;
int y=match[x],d=INF;
// 对于当前节点y,bfs有连边的下一点
for(int i=1;i<=m;i++)
{
if(!vis[i])
{
if(slack[i]>val1[y]+val2[i]-favor[y][i])
{
slack[i]=val1[y]+val2[i]-favor[y][i];
pre[i]=x;
}
if(slack[i]<d)
{
d=slack[i];
nex=i;
}
}
}
for(int i=0;i<=m;i++)
{
if(vis[i])
val1[match[i]]-=d,val2[i]+=d;
else
slack[i]-=d;
}
x=nex;
}while(match[x]);
// pre数组对bfs访问路径进行记录,在最后一并改变match
while(x)
{
match[x]=match[pre[x]];
x=pre[x];
}
}
int KM()
{
memset(match,0,sizeof match);
memset(val1,0,sizeof val1);
memset(val2,0,sizeof val2);
for(int i=1;i<=n;i++)
{
memset(vis,false,sizeof vis);
bfs(i);
}
int res=0;
for(int i=1;i<=m;i++)
res+=favor[match[i]][i];
return res;
}
int main()
{
while(scanf("%d",&n)!=EOF)
{
m=n;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&favor[i][j]);
printf("%d
",KM());
}
return 0;
}
E - Assignment
题意
有(n)个连的军队以及(m)个任务((mge n))
每个连的军队只能完成一项任务,每个任务也只能由一个连的军队来完成
如果第(i)连的军队选择完成第(j)项任务,那么完成的效率则为(E_{i,j})
现在已经有了每连军队的分配方案,而现在我们想要更改某些军队的任务,以使得效率总和最大化,同时还要保证被修改任务的军队数量尽可能少
输出改变任务的军队的最少数量,以及改变后总效率的最大增量
标签
二分图最大权完美匹配(原图增广)
思路
由于还要求增量以及尽可能少的更改数量
可以将所有边权乘以(n+1)(或更大的一个数),发现原先边权大的处理后仍然较大
然后将所有原先已经选中的边的边权(+1),表示原先的边如果能选就尽可能去选(总共(n)条匹配边,要保证缩放对答案不会造成影响)
跑KM算法,求出当前的最大匹配值:这个值对(n+1)取模得到的值即原边选中的数量((+1)的边数),而除以(n+1)得到的值即题目最大解(乘数取(n+1)来保证边权(+1)对这部分答案无影响)
来源
2009 Multi-University Training Contest 5 - Host by NUDT
代码
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int N=55;
int n,m,match[N];
bool vis1[N],vis2[N];
int favor[N][N];
int val1[N],val2[N],slack[N];
bool dfs(int p)
{
vis1[p]=true;
for(int i=1;i<=m;i++)
if(!vis2[i])
{
if(val1[p]+val2[i]==favor[p][i])
{
vis2[i]=true;
if(!match[i]||dfs(match[i]))
{
match[i]=p;
return true;
}
}
else
slack[i]=min(slack[i],val1[p]+val2[i]-favor[p][i]);
}
return false;
}
int KM()
{
for(int i=1;i<=n;i++)
{
val1[i]=-INF;
for(int j=1;j<=m;j++)
val1[i]=max(val1[i],favor[i][j]);
}
memset(match,0,sizeof match);
memset(val2,0,sizeof val2);
for(int i=1;i<=n;i++)
{
memset(slack,INF,sizeof slack);
while(true)
{
memset(vis1,false,sizeof vis1);
memset(vis2,false,sizeof vis2);
if(dfs(i))
break;
int d=INF;
for(int j=1;j<=m;j++)
if(!vis2[j])
d=min(d,slack[j]);
for(int j=1;j<=n;j++)
if(vis1[j])
val1[j]-=d;
for(int j=1;j<=m;j++)
if(vis2[j])
val2[j]+=d;
}
}
int res=0;
for(int i=1;i<=m;i++)
if(match[i])
res+=favor[match[i]][i];
return res;
}
int main()
{
while(scanf("%d%d",&n,&m)!=EOF)
{
//让所有边权乘以n+1
int k=n+1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d",&favor[i][j]);
favor[i][j]*=k;
}
}
int sum=0;
for(int i=1;i<=n;i++)
{
int d;
scanf("%d",&d);
sum+=favor[i][d]/k;
// 对于所有原边,+1使其能够优先被使用
favor[i][d]++;
}
// 最后得到的匹配值,%(n+1)表示选择的原边数,/(n+1)表示原题意总值
int res=KM();
printf("%d %d
",n-res%k,res/k-sum);
}
return 0;
}
F - Cordon Bleu
题意
有一个企业家刚开了家餐厅,但不知道应该搭配什么葡萄酒,所以企业家打算先品尝所有酒庄的葡萄酒。
在二位平面上有(N)个点,表示不同的酒庄的位置;还有(M)个点,表示不同快递员初始时所在的位置;最后一个点表示餐厅所在的位置。
如果一位快递员只送一次酒,那么他的路线应是初始位置 - 酒庄 - 餐厅。
如果一位快递员要送多次酒,限制他每次只能够送一瓶,即路线应是初始位置 - 酒庄(1) - 餐厅 - 酒庄(2) - 餐厅……如此循环下去。
快递员能够获得的报酬是每段路的曼哈顿距离之和。
现在企业家想让一些快递员把每个酒庄的酒各送一瓶到酒店(同一个快递员可以雇佣多次,配送路线如上所述),询问企业家的最小花费是多少?
标签
二分图最小权完美匹配
思路
以下为官方题解内容

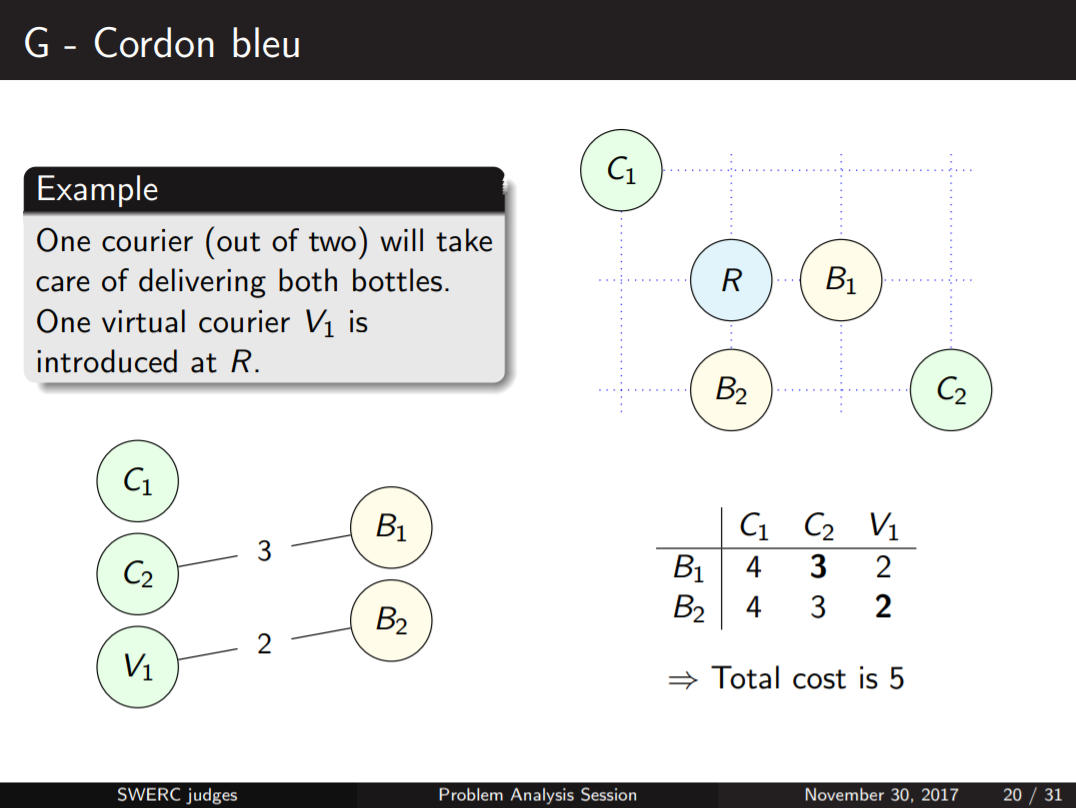
首先,注意到所有酒都是必须要送到餐馆的,所以所有酒庄到餐馆的曼哈顿距离和可以直接先计算出来并加入答案中
考虑快递员的配送:由于快递员把酒送到餐馆之后,坐标就可以当作与餐馆重合了,所以我们可以将餐馆也视作快递员
将快递员与餐馆作为二分图左部,酒庄作为二分图右部,两集合间边的边权即点到点的曼哈顿距离
如果在匹配过程中,酒庄选择了餐馆作为匹配对象,那也就意味着选择了一位已经到达餐馆的快递员前往配送,所以餐馆应该是能够被匹配多次的
初始状态下是没有快递员在餐馆的(即使坐标重合,也是餐馆归餐馆,快递员归快递员),所以为了保证酒庄匹配到餐馆时至少有一名快递员在餐馆,我们只能建立(n-1)个代表餐馆的虚点作为酒庄的匹配对象
所以这张二分图左侧应有(m+n-1)个点,表示快递员与餐馆的虚点,右侧应有(n)个点,表示酒庄;最终所有酒庄应当达到完美匹配状态
最后,由于求的是最小权完美匹配,故对所有边权取反跑KM算法
来源
2017-2018 ACM-ICPC Southwestern European Regional Programming Contest (SWERC 2017)
代码
注意(long long)即可,KM两种写法均可通过
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll LINF=0x3f3f3f3f3f3f3f3f;
const int N=2005;
int n,m,match[N],pre[N];
bool vis[N];
int favor[N][N];
ll val1[N],val2[N],slack[N];
void bfs(int p)
{
memset(pre,0,sizeof pre);
memset(slack,LINF,sizeof slack);
int x=0,nex=0;
match[0]=p;
do{
vis[x]=true;
int y=match[x];
ll d=LINF;
for(int i=1;i<=m;i++)
{
if(!vis[i])
{
if(slack[i]>val1[y]+val2[i]-favor[y][i])
{
slack[i]=val1[y]+val2[i]-favor[y][i];
pre[i]=x;
}
if(slack[i]<d)
{
d=slack[i];
nex=i;
}
}
}
for(int i=0;i<=m;i++)
{
if(vis[i])
val1[match[i]]-=d,val2[i]+=d;
else
slack[i]-=d;
}
x=nex;
}while(match[x]);
while(x)
{
match[x]=match[pre[x]];
x=pre[x];
}
}
ll KM()
{
memset(match,0,sizeof match);
memset(val1,0,sizeof val1);
memset(val2,0,sizeof val2);
for(int i=1;i<=n;i++)
{
memset(vis,false,sizeof vis);
bfs(i);
}
ll res=0;
for(int i=1;i<=m;i++)
res+=favor[match[i]][i];
return res;
}
struct Point
{
int x,y;
int distance(Point p)
{
return abs(x-p.x)+abs(y-p.y);
}
};
Point bott[1005],cour[1005],rest;
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d%d",&bott[i].x,&bott[i].y);
for(int i=1;i<=m;i++)
scanf("%d%d",&cour[i].x,&cour[i].y);
scanf("%d%d",&rest.x,&rest.y);
for(int i=1;i<=n;i++)
{
// 注意对边权取反
for(int j=1;j<=m;j++)
favor[i][j]=-bott[i].distance(cour[j]);
// 虚点
for(int j=m+1,k=1;k<n;j++,k++)
favor[i][j]=-bott[i].distance(rest);
}
// 虚点数量
m+=n-1;
// 直接处理所有酒庄到餐馆的manhattan距离
ll ans=0;
for(int i=1;i<=n;i++)
ans+=rest.distance(bott[i]);
printf("%lld
",ans-KM());
return 0;
}
G - Flow Problem
题意
给定(n)个点(m)条边,求点(1)至点(n)的最大流
标签
最大流
思路
最大流 - Dinic算法模板题
来源
HyperHexagon's Summer Gift (Original tasks)
代码
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=30,maxm=2000;
struct edge{
int u,v,cap,flow;
edge(){}
edge(int u,int v,int cap,int flow):u(u),v(v),cap(cap),flow(flow){}
}eg[maxm<<1];
int tot,dis[maxn<<1],cur[maxn<<1];
vector<int> tab[maxn<<1];
void init(int n){
tot=0;
while(n)tab[n--].clear();
}
void addedge(int u,int v,int cap){
tab[u].push_back(tot);
eg[tot++]=edge(u,v,cap,0);
tab[v].push_back(tot);
eg[tot++]=edge(v,u,0,0);
}
int bfs(int s,int t){
queue<int> q;
q.push(s);
memset(dis,INF,sizeof dis);
dis[s]=0;
while(!q.empty()){
int h=q.front(),i;
q.pop();
for(i=0;i<tab[h].size();i++){
edge &e=eg[tab[h][i]];
if(e.cap>e.flow&&dis[e.v]==INF){
dis[e.v]=dis[h]+1;
q.push(e.v);
}
}
}
return dis[t]<INF;
}
int dfs(int x,int maxflow,int s,int t){
if(x==t||maxflow==0)
return maxflow;
int flow=0,i,f;
for(i=cur[x];i<tab[x].size();i++){
cur[x]=i;
edge &e=eg[tab[x][i]];
if(dis[e.v]==dis[x]+1&&(f=dfs(e.v,min(maxflow,e.cap-e.flow),s,t))>0){
e.flow+=f;
eg[tab[x][i]^1].flow-=f;
flow+=f;
maxflow-=f;
if(maxflow==0)
break;
}
}
return flow;
}
int dinic(int s,int t){
int flow=0;
while(bfs(s,t)){
memset(cur,0,sizeof(cur));
flow+=dfs(s,INF,s,t);
}
return flow;
}
void solve(int cas)
{
int n,m;
scanf("%d%d",&n,&m);
init(n);
for(int i=1;i<=m;i++)
{
int u,v,c;
scanf("%d%d%d",&u,&v,&c);
addedge(u,v,c);
}
printf("Case %d: %d
",cas,dinic(1,n));
}
int main()
{
int T;
scanf("%d",&T);
for(int t=1;t<=T;t++)
solve(t);
return 0;
}
H - Food
题意
(N)个人,(F)种食物,(D)种饮料
每种食物或者饮料提供了多份,但每个人只能分别拿一份
每个人可能只喜欢某些食物或饮料,如果一个人同时获得了自己喜欢的食物或饮料,那么他将会满足
问最多可以让多少人能够满足
标签
最大流
思路
以源点 - 食物 - 人 - 饮料 - 汇点的顺序进行建图
“每种食物或饮料提供了多份”,可以限制源点 - 食物和饮料 - 汇点之间的流量来实现
“每个人只能分别拿一份”,这里就需要将人进行拆点,通过拆点后连边限制边权为(1)进行实现
同时对于每个人喜欢的食物与饮料,从对应点向人进行连边并限制流量为(1)即可
最后整张图的最大流即表示最多满足的人数
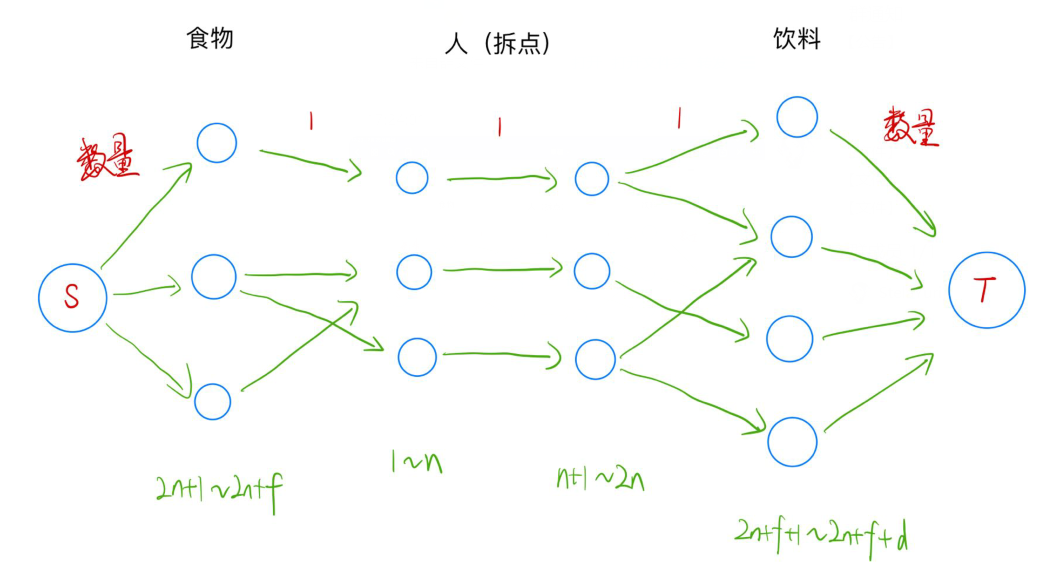
来源
2012 ACM/ICPC Asia Regional Chengdu Online
代码
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=805,maxm=100000;
struct edge{
int u,v,cap,flow;
edge(){}
edge(int u,int v,int cap,int flow):u(u),v(v),cap(cap),flow(flow){}
}eg[maxm<<1];
int tot,dis[maxn<<1],cur[maxn<<1];
vector<int> tab[maxn<<1];
void init(int n){
tot=0;
while(n)tab[n--].clear();
}
void addedge(int u,int v,int cap){
tab[u].push_back(tot);
eg[tot++]=edge(u,v,cap,0);
tab[v].push_back(tot);
eg[tot++]=edge(v,u,0,0);
}
int bfs(int s,int t){
queue<int> q;
q.push(s);
memset(dis,INF,sizeof dis);
dis[s]=0;
while(!q.empty()){
int h=q.front(),i;
q.pop();
for(i=0;i<tab[h].size();i++){
edge &e=eg[tab[h][i]];
if(e.cap>e.flow&&dis[e.v]==INF){
dis[e.v]=dis[h]+1;
q.push(e.v);
}
}
}
return dis[t]<INF;
}
int dfs(int x,int maxflow,int s,int t){
if(x==t||maxflow==0)
return maxflow;
int flow=0,i,f;
for(i=cur[x];i<tab[x].size();i++){
cur[x]=i;
edge &e=eg[tab[x][i]];
if(dis[e.v]==dis[x]+1&&(f=dfs(e.v,min(maxflow,e.cap-e.flow),s,t))>0){
e.flow+=f;
eg[tab[x][i]^1].flow-=f;
flow+=f;
maxflow-=f;
if(maxflow==0)
break;
}
}
return flow;
}
int dinic(int s,int t){
int flow=0;
while(bfs(s,t)){
memset(cur,0,sizeof(cur));
flow+=dfs(s,INF,s,t);
}
return flow;
}
int main()
{
int N,F,D;
char str[205];
while(scanf("%d%d%d",&N,&F,&D)!=EOF)
{
int s=2*N+F+D+1,t=2*N+F+D+2;
init(2*N+F+D+2);
// 限制每个人只能够拿一份
for(int i=1;i<=N;i++)
addedge(i,N+i,1);
for(int i=1;i<=F;i++)
{
int d;
scanf("%d",&d);
// 食物与源点相连,限制流量
addedge(s,2*N+i,d);
}
for(int i=1;i<=D;i++)
{
int d;
scanf("%d",&d);
// 饮料与汇点相连,限制流量
addedge(2*N+F+i,t,d);
}
for(int i=1;i<=N;i++)
{
scanf("%s",str+1);
// 从食物连向牛
for(int j=1;j<=F;j++)
if(str[j]=='Y')
addedge(2*N+j,i,1);
}
for(int i=1;i<=N;i++)
{
scanf("%s",str+1);
// 从牛连向饮料
for(int j=1;j<=D;j++)
if(str[j]=='Y')
addedge(N+i,2*N+F+j,1);
}
printf("%d
",dinic(s,t));
}
return 0;
}
I - Avoiding the Apocalypse
题意
你和你的团队在这座城市开始了僵尸启示录,你们都被僵尸病毒感染了
这座城市共有(n)个点,你们总共有(g)个人,初始时所有人都在起始点(i),僵尸病毒会在(t)个单位时间后才发作,所以你们需要尽快赶往任意的医疗机构进行治疗;城市内共有(m)个点属于医疗机构
城市内道路总共有(r)条,每条道路都是单向的,一个单位时间只能够进(p_i)个人,并且需要(t_i)个单位时间才能走完这条路
问(t)秒后最多能有多少人到达医疗机构接受治疗
标签
最大流(分层建图)
思路
按时间分层,加上初始状态总共分(t+1)层,每层(n)个点表示原图的点,故整张图总共有(n(t+1)+2)个点
初始状态下,所有(g)个人都在起始点(i),所以从源点向第(0)层的起始点(i)连一条容量为(g)的边
由于终点有(m)个,所以第(t)层的这(m)个点向汇点连一条不限容量的边(总容量已由源点边确定)
其后,对于每一层,遍历一遍途中所有的路径
“(u_i ightarrow v_i)边单位时间内只能通过(p_i)个人,并且需要(t_i)个单位时间才能走完”,表示这是一条容量为(p_i),时间跨度为(t_i)的边
所以可以枚举每一层作为起始时间,假如当前在处理第(j)层,那么这条边就是指从第(j)层的(u_i)点向第(j+t_i)层的(v_i)点可以连一条容量为(p_i)的边
最后,在某些点的人可以选择当前这段时间内哪也不走(理论上只有在走到终点后才会出现这种情况),所以对于每一层(j (0le jlt t))的每一点,都需要向(j+1)层的对应点连一条不限容量的边
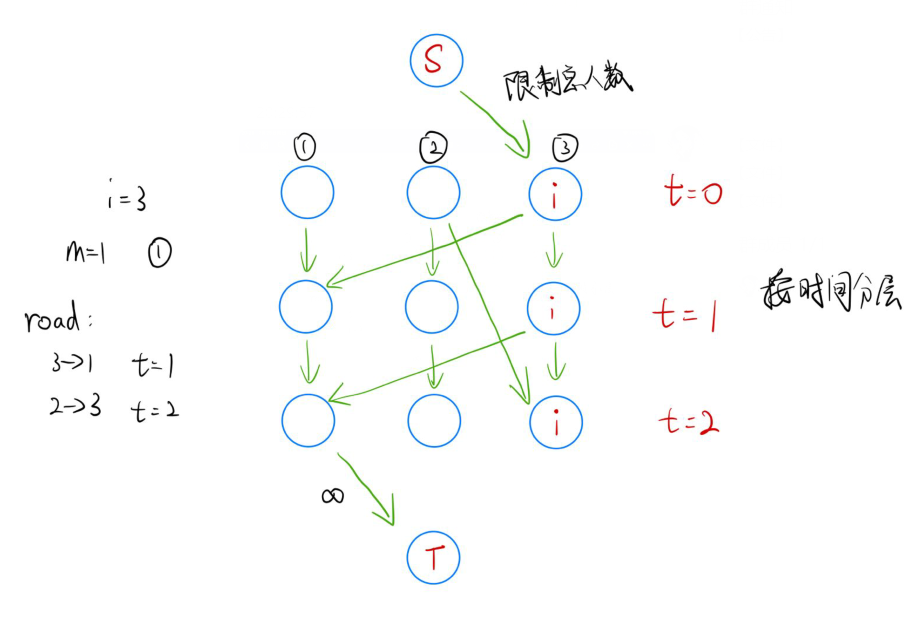
来源
2014 Benelux Algorithm Programming Contest (BAPC 14)
代码
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=100050,maxm=200050;
struct edge{
int u,v,cap,flow;
edge(){}
edge(int u,int v,int cap,int flow):u(u),v(v),cap(cap),flow(flow){}
}eg[maxm<<1];
int tot,dis[maxn<<1],cur[maxn<<1];
vector<int> tab[maxn<<1];
void init(int n){
tot=0;
while(n)tab[n--].clear();
}
void addedge(int u,int v,int cap){
tab[u].push_back(tot);
eg[tot++]=edge(u,v,cap,0);
tab[v].push_back(tot);
eg[tot++]=edge(v,u,0,0);
}
int bfs(int s,int t){
queue<int> q;
q.push(s);
memset(dis,INF,sizeof dis);
dis[s]=0;
while(!q.empty()){
int h=q.front(),i;
q.pop();
for(i=0;i<tab[h].size();i++){
edge &e=eg[tab[h][i]];
if(e.cap>e.flow&&dis[e.v]==INF){
dis[e.v]=dis[h]+1;
q.push(e.v);
}
}
}
return dis[t]<INF;
}
int dfs(int x,int maxflow,int s,int t){
if(x==t||maxflow==0)
return maxflow;
int flow=0,i,f;
for(i=cur[x];i<tab[x].size();i++){
cur[x]=i;
edge &e=eg[tab[x][i]];
if(dis[e.v]==dis[x]+1&&(f=dfs(e.v,min(maxflow,e.cap-e.flow),s,t))>0){
e.flow+=f;
eg[tab[x][i]^1].flow-=f;
flow+=f;
maxflow-=f;
if(maxflow==0)
break;
}
}
return flow;
}
int dinic(int s,int t){
int flow=0;
while(bfs(s,t)){
memset(cur,0,sizeof(cur));
flow+=dfs(s,INF,s,t);
}
return flow;
}
struct Edge
{
int u,v,cnt,tim;
}road[1010];
int n;
int endcity[1010];
// 获取第lay层的id城市编号
inline int getid(int lay,int id)
{
return lay*n+id;
}
void solve()
{
scanf("%d",&n);
int st,cnt,tim;
scanf("%d%d%d",&st,&cnt,&tim);
int m;
scanf("%d",&m);
for(int i=1;i<=m;i++)
scanf("%d",&endcity[i]);
int r;
scanf("%d",&r);
for(int i=1;i<=r;i++)
scanf("%d%d%d%d",&road[i].u,&road[i].v,&road[i].cnt,&road[i].tim);
int S=n*(tim+1)+1,T=n*(tim+1)+2;
init(n*(tim+1)+2);
// 源点连向起始城市,流量为人数
addedge(
S,
getid(0,st),
cnt
);
// tim秒后,终点城市连向汇点,不限制流量
for(int i=1;i<=m;i++)
addedge(
getid(tim,endcity[i]),
T,
INF
);
for(int t=0;t<tim;t++)
{
// 连向road[i].tim时间后的层,流量限制为road[i].cnt
for(int i=1;i<=r;i++)
if(t+road[i].tim<=tim)
addedge(
getid(t,road[i].u),
getid(t+road[i].tim,road[i].v),
road[i].cnt
);
// 保留属性至下一层
for(int i=1;i<=n;i++)
addedge(
getid(t,i),
getid(t+1,i),
INF
);
}
printf("%d
",dinic(S,T));
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
solve();
return 0;
}
J - Leapin' Lizards
题意
给定一个石柱网格,每个位置都有一根一定高度的石柱,其中某些位置初始时有一只蜥蜴
所有蜥蜴单步跳跃距离最远为(d)(距离为曼哈顿距离)
如果一只蜥蜴能够在某次跳跃中跳出网格,那么它就能够成功逃脱
如果某只蜥蜴跳离了某根石柱,那么这根石柱会在它跳离后高度(-1),如果高度变为(0)则后续不能再有蜥蜴能够跳到这根石柱上;在同一时间内不能有两只及以上的蜥蜴位于同一根石柱上
问最终最少有多少只蜥蜴跳不出这张网格
标签
最大流(拆点)
思路
根据题意,每根石柱最多能被蜥蜴经过“高度”次
而每只蜥蜴最远跳跃距离为(d),所以每个点需要向其距离不大于(d)的所有点进行连边,不限容量
而对于每个石柱,需要将点权转化为边权,即进行拆点,让拆分后的两点(a ightarrow b)进行连线,限制容量为石柱的高度
拆点后对于不同石柱间的连线,则需要保证跳出点的流量经过了拆点后两点间连的边,所以(i)柱连向(j)柱对应的点也就是(b_i ightarrow a_j)
最后考虑源点汇点,将源点向所有初始时存在一只蜥蜴的点({a_i})连边,容量为(1)表示这一只蜥蜴;所有能够直接跳出网格图的点({b_i})向汇点连边,不限容量
最后得到的最大流就是能够逃脱的蜥蜴数量,用总数量减去即为解
来源
Mid-Central USA 2005
代码
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=1000,maxm=5000;
struct edge{
int u,v,cap,flow;
edge(){}
edge(int u,int v,int cap,int flow):u(u),v(v),cap(cap),flow(flow){}
}eg[maxm<<1];
int tot,dis[maxn<<1],cur[maxn<<1];
vector<int> tab[maxn<<1];
void init(int n){
tot=0;
while(n)tab[n--].clear();
}
void addedge(int u,int v,int cap){
tab[u].push_back(tot);
eg[tot++]=edge(u,v,cap,0);
tab[v].push_back(tot);
eg[tot++]=edge(v,u,0,0);
}
int bfs(int s,int t){
queue<int> q;
q.push(s);
memset(dis,INF,sizeof dis);
dis[s]=0;
while(!q.empty()){
int h=q.front(),i;
q.pop();
for(i=0;i<tab[h].size();i++){
edge &e=eg[tab[h][i]];
if(e.cap>e.flow&&dis[e.v]==INF){
dis[e.v]=dis[h]+1;
q.push(e.v);
}
}
}
return dis[t]<INF;
}
int dfs(int x,int maxflow,int s,int t){
if(x==t||maxflow==0)
return maxflow;
int flow=0,i,f;
for(i=cur[x];i<tab[x].size();i++){
cur[x]=i;
edge &e=eg[tab[x][i]];
if(dis[e.v]==dis[x]+1&&(f=dfs(e.v,min(maxflow,e.cap-e.flow),s,t))>0){
e.flow+=f;
eg[tab[x][i]^1].flow-=f;
flow+=f;
maxflow-=f;
if(maxflow==0)
break;
}
}
return flow;
}
int dinic(int s,int t){
int flow=0;
while(bfs(s,t)){
memset(cur,0,sizeof(cur));
flow+=dfs(s,INF,s,t);
}
return flow;
}
char mpa[30][30],mpb[30][30];
int n,m,d;
// 第l层点x,y的id
inline int id(int x,int y,int l)
{
return (x-1)*m+y+l*n*m;
}
void solve(int cas)
{
scanf("%d%d",&n,&d);
for(int i=1;i<=n;i++)
scanf("%s",mpa[i]+1);
for(int i=1;i<=n;i++)
scanf("%s",mpb[i]+1);
m=strlen(mpa[1]+1);
int s=n*m*2+1,t=n*m*2+2;
init(n*m*2+2);
int cnt=0;
// 源点与蜥蜴连边,容量为1
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(mpb[i][j]=='L')
{
addedge(s,id(i,j,0),1);
cnt++;
}
// 拆点连边,容量为原点权
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(mpa[i][j]!='0')
addedge(id(i,j,0),id(i,j,1),mpa[i][j]-'0');
// 跳跃路线连边
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(i-d<1||j-d<1||i+d>n||j+d>m)
{
addedge(id(i,j,1),t,INF);
continue;
}
for(int x=i-d;x<=i+d;x++)
for(int y=j-d;y<=j+d;y++)
{
if(x==i&&y==j||abs(x-i)+abs(y-j)>d)
continue;
addedge(id(i,j,1),id(x,y,0),INF);
}
}
printf("Case #%d: ",cas);
int ans=cnt-dinic(s,t);
if(ans==0)
printf("no lizard was");
else if(ans==1)
printf("1 lizard was");
else
printf("%d lizards were",ans);
printf(" left behind.
");
}
int main()
{
int T;
scanf("%d",&T);
for(int t=1;t<=T;t++)
solve(t);
return 0;
}
K - Route Redundancy
题意
给定一张(n)个点(m)条边的有向图,边具有流量限制,给定起点与终点
问整张图从起点到终点的“最大总流量”与“单条路径的最大流量”的比值是多少
标签
最大流(寻找单路线最大流)
思路
先根据要求建图跑一遍最大流,最大总流量便能求出
“单条路径的最大流量”也就是此时网络中从起点到终点的最长路,搜索即可
来源
2011 Greater New York Regional
代码
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=2000,maxm=10000;
struct edge{
int u,v,cap,flow;
edge(){}
edge(int u,int v,int cap,int flow):u(u),v(v),cap(cap),flow(flow){}
}eg[maxm<<1];
int tot,dis[maxn<<1],cur[maxn<<1];
vector<int> tab[maxn<<1];
void init(int n){
tot=0;
while(n)tab[n--].clear();
}
void addedge(int u,int v,int cap){
tab[u].push_back(tot);
eg[tot++]=edge(u,v,cap,0);
tab[v].push_back(tot);
eg[tot++]=edge(v,u,0,0);
}
int bfs(int s,int t){
queue<int> q;
q.push(s);
memset(dis,INF,sizeof dis);
dis[s]=0;
while(!q.empty()){
int h=q.front(),i;
q.pop();
for(i=0;i<tab[h].size();i++){
edge &e=eg[tab[h][i]];
if(e.cap>e.flow&&dis[e.v]==INF){
dis[e.v]=dis[h]+1;
q.push(e.v);
}
}
}
return dis[t]<INF;
}
int dfs(int x,int maxflow,int s,int t){
if(x==t||maxflow==0)
return maxflow;
int flow=0,i,f;
for(i=cur[x];i<tab[x].size();i++){
cur[x]=i;
edge &e=eg[tab[x][i]];
if(dis[e.v]==dis[x]+1&&(f=dfs(e.v,min(maxflow,e.cap-e.flow),s,t))>0){
e.flow+=f;
eg[tab[x][i]^1].flow-=f;
flow+=f;
maxflow-=f;
if(maxflow==0)
break;
}
}
return flow;
}
int dinic(int s,int t){
int flow=0;
while(bfs(s,t)){
memset(cur,0,sizeof(cur));
flow+=dfs(s,INF,s,t);
}
return flow;
}
int Dist[maxn];
void DFS(int u)
{
// 检查所有u点出发的边
for(int &e:tab[u])
{
int &v=eg[e].v;
// 检查当前这条路的实际流量 Dist[v]<=Dist[u] 注意反向边影响
int f=min(eg[e].flow,Dist[u]);
// 如果这条路的流量比原先流量大,更新
if(Dist[v]<f)
{
Dist[v]=f;
DFS(v);
}
}
}
void solve()
{
int D,n,m,a,b;
scanf("%d%d%d%d%d",&D,&n,&m,&a,&b);
a++,b++;
init(n);
for(int i=1;i<=m;i++)
{
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
u++,v++;
addedge(u,v,w);
}
// 先跑最大流,将网络构造出来
int maxflow=dinic(a,b);
// 在网络中寻找最长路,假设源点流量无限
memset(Dist,-1,sizeof Dist);
Dist[a]=INF;
DFS(a);
printf("%d %.3f
",D,1.0*maxflow/Dist[b]);
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
solve();
return 0;
}
L - Path
题意
给定(n)个点(m)条边的一张有向图
Jerry每次都会沿着最短路从(1)号点走到(n)号点
现在Tom想断掉某些路,使得Jerry必须走更长的路,断掉一条路径的花费即该路的长度
问Tom的最小花费
标签
最短路、最小割
思路
Jerry只会沿着最短路行走,所以可以通过最短路算法,以(1)作为起点搜索出所有最短路径((u ightarrow v, dist[u]+w=dist[v]))
借助这些处理出的最短路重新建图,构建出网络
在网络图中,我们需要用最小的花费使得源点与汇点不连通,显而易见就是求最小割
最小割(=)最大流,跑最大流算法即可
来源
2019 Multi-University Training Contest 1
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> P;
const int INF=0x3f3f3f3f;
const ll LINF=0x3f3f3f3f3f3f3f3f;
const int maxn=10010,maxm=10010;
struct edge{
int u,v;
ll cap,flow;
edge(){}
edge(int u,int v,int cap,int flow):u(u),v(v),cap(cap),flow(flow){}
}eg[maxm<<1];
int tot,dis[maxn<<1],cur[maxn<<1];
vector<int> tab[maxn<<1];
void init(int n){
tot=0;
while(n)tab[n--].clear();
}
void addedge(int u,int v,ll cap){
tab[u].push_back(tot);
eg[tot++]=edge(u,v,cap,0);
tab[v].push_back(tot);
eg[tot++]=edge(v,u,0,0);
}
ll bfs(int s,int t){
queue<int> q;
q.push(s);
memset(dis,INF,sizeof dis);
dis[s]=0;
while(!q.empty()){
int h=q.front(),i;
q.pop();
for(i=0;i<tab[h].size();i++){
edge &e=eg[tab[h][i]];
if(e.cap>e.flow&&dis[e.v]==INF){
dis[e.v]=dis[h]+1;
q.push(e.v);
}
}
}
return dis[t]<INF;
}
ll dfs(int x,ll maxflow,int s,int t){
if(x==t||maxflow==0)
return maxflow;
ll flow=0,f;
for(int i=cur[x];i<tab[x].size();i++){
cur[x]=i;
edge &e=eg[tab[x][i]];
if(dis[e.v]==dis[x]+1&&(f=dfs(e.v,min(maxflow,e.cap-e.flow),s,t))>0){
e.flow+=f;
eg[tab[x][i]^1].flow-=f;
flow+=f;
maxflow-=f;
if(maxflow==0)
break;
}
}
return flow;
}
ll dinic(int s,int t){
ll flow=0;
while(bfs(s,t)){
memset(cur,0,sizeof(cur));
flow+=dfs(s,LINF,s,t);
}
return flow;
}
vector<P> G[maxn];
ll dist[maxn];
void dijkstra(int st){
priority_queue<P> pq;
memset(dist,LINF,sizeof dist);
dist[st]=0;pq.push(P(0,st));
while(!pq.empty()){
int v=pq.top().second;pq.pop();
for(P pd:G[v])if(dist[v]+pd.second<dist[pd.first])
dist[pd.first]=dist[v]+pd.second,pq.push(P(-dist[pd.first],pd.first));
}
}
void solve()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
G[i].clear();
for(int i=1;i<=m;i++)
{
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
G[u].push_back(P(v,w));
}
dijkstra(1);
init(n);
for(int i=1;i<=n;i++)
{
// 将最短路边加入网络
for(P &pd:G[i])
if(dist[pd.first]==dist[i]+pd.second)
addedge(i,pd.first,pd.second);
}
printf("%lld
",dinic(1,n));
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
solve();
return 0;
}
M - Mining Station on the Sea
题意
有(n)艘船,(n)个港口与(m)个钻井平台,每艘船初始时都位于某个钻井平台中
有(k)条边,每条边连接两个钻井平台(a,b),表示这两个钻井平台互相可以直接通行,距离为(c)
还有(p)条边,每条边连接某港口(d)与某钻井平台(e),距离为(f)
现在每艘船都需要找一个港口停船,每个港口也只能够停一艘船,试着找出一个分配方案使得所有船到对应港口的距离总和最小
注意一旦某艘船进入了港口后,它就不会再出来
标签
最小费用最大流
思路
按题意建边,然后每次对于每艘船初始时所在的钻井平台跑一次最短路(注意钻井平台与港口之间连接的应是单向边)
跑完最短路后,设船(i)所在的钻井平台是(belong[i]),则对于所有从(belong[i])出发所可以到达的港口(j),直接进行连边,限制流量为(1)(表示只考虑目前这一艘船),花费为(belong[i] ightarrow j)的最短路距离
对于超级源点,向所有船(i)所在的钻井平台(belong[i])建边,限制流量为(1)(只考虑一艘船,可重边),花费为(0)
对于所有港口,向超级汇点连边,限制流量为(1)(每个港口只能停一艘船),花费为(0)
类似二分图最小权完美匹配,保证这张图能够跑出最大匹配,得到的费用即最小费用
来源
2008 Asia Regional Harbin
代码
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> P;
const int INF=0x3f3f3f3f;
const int maxn=500;
struct MCMF {
struct E {
int from, to, cap, v;
E() {}
E(int f, int t, int cap, int v) : from(f), to(t), cap(cap), v(v) {}
};
int n, m, s, t;
vector<E> edges;
vector<int> G[maxn];
bool inq[maxn];
int dis[maxn], pre[maxn], a[maxn];
void init(int _n, int _s, int _t) {
n = _n; s = _s; t = _t;
for (int i = 0; i <= n; i++)
G[i].clear();
edges.clear();
m = 0;
}
void add(int from, int to, int cap, int cost) {
edges.emplace_back(from, to, cap, cost);
edges.emplace_back(to, from, 0, -cost);
G[from].push_back(m++);
G[to].push_back(m++);
}
bool spfa() {
for (int i = 0; i <= n; i++) {
dis[i] = 1e9;
pre[i] = -1;
inq[i] = false;
}
dis[s] = 0, a[s] = 1e9, inq[s] = true;
queue<int> Q; Q.push(s);
while (!Q.empty()) {
int u = Q.front(); Q.pop();
inq[u] = false;
for (int& idx: G[u]) {
E& e = edges[idx];
if (e.cap && dis[e.to] > dis[u] + e.v) {
dis[e.to] = dis[u] + e.v;
pre[e.to] = idx;
a[e.to] = min(a[u], e.cap);
if (!inq[e.to]) {
inq[e.to] = true;
Q.push(e.to);
}
}
}
}
return pre[t] != -1;
}
int solve() {
int flow = 0, cost = 0;
while (spfa()) {
flow += a[t];
cost += a[t] * dis[t];
int u = t;
while (u != s) {
edges[pre[u]].cap -= a[t];
edges[pre[u] ^ 1].cap += a[t];
u = edges[pre[u]].from;
}
}
return cost;
}
}f;
int belong[maxn];
vector<P> G[maxn];
int dist[maxn];
void dijkstra(int st){
priority_queue<P> pq;
memset(dist,INF,sizeof dist);
dist[st]=0;pq.push(P(0,st));
while(!pq.empty()){
int v=pq.top().second;pq.pop();
for(P pd:G[v])if(dist[v]+pd.second<dist[pd.first])
dist[pd.first]=dist[v]+pd.second,pq.push(P(-dist[pd.first],pd.first));
}
}
int main()
{
int n,m,k,p;
while(scanf("%d%d%d%d",&n,&m,&k,&p)!=EOF)
{
f.init(n+m+2,n+m+1,n+m+2);
for(int i=1;i<=n+m;i++)
G[i].clear();
for(int i=1;i<=n;i++)
scanf("%d",&belong[i]);
for(int i=1;i<=k;i++)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
G[a].push_back(P(b,c));
G[b].push_back(P(a,c));
}
for(int i=1;i<=p;i++)
{
int d,e,f;
scanf("%d%d%d",&d,&e,&f);
G[e].push_back(P(d+m,f)); //单向边
}
for(int i=1;i<=n;i++)
{
f.add(f.s,belong[i],1,0);
f.add(j+m,f.t,1,0);
dijkstra(belong[i]);
for(int j=1;j<=n;j++)
{
if(dist[j+m]==INF)
continue;
// 每条船对应的station向可达的port连边,边权为最短路
f.add(belong[i],j+m,INF,dist[j+m]);
}
}
printf("%d
",f.solve());
}
return 0;
}
N - Special Fish
题意
有(n)只鱼,每只鱼都有一个权值(value_i)
每只鱼都认为自己是雄性,并且它们会去攻击自己认为是雌性的其他鱼
一旦第(i)只鱼攻击了第(j)只鱼,则会产出数量为(value_i oplus value_j)的卵
每条鱼最多只能被攻击一次,也最多只能主动攻击一次
问产卵数量的最大可能总和
标签
最大费用流
思路
对于每只鱼,考虑进行拆点,拆为“攻击点”与“被攻击点”
源点向所有鱼的“攻击点”连边,容量为(1)费用为(0),限制每条鱼只能攻击一次
所有鱼的“被攻击点”向汇点连边,容量为(1)费用为(0),限制每条鱼只能被攻击一次
考虑所有可能会进行攻击的二元组((i,j))((i)可能攻击(j)),则将(i)的“攻击点”向(j)的被攻击点连边,容量为(1)表示只攻击一次,费用为(-(value_i oplus value_j)),目的是求出最大费用
到这里就结束的话,直接跑MCMF板子答案是错的
发现最小费用最大流是建立在“最大流”的限制上,而在本题中没有要求必须取到最大匹配;因此,如果强制取到最大匹配,答案可能会变小,如下图所示(值取反)
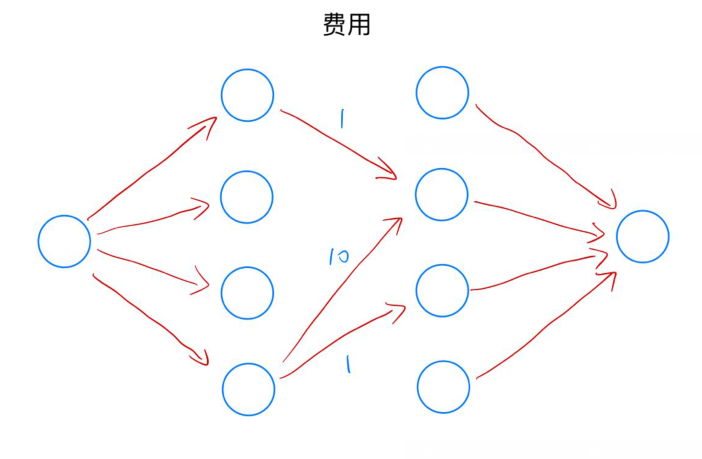
上图中,整张图最大流量为(2),这是建立在不流经费用为(-10)的前提下,而明显本题选择这条边作为答案更为合适
为解决这一问题,我们考虑让所有鱼能够有“放弃攻击”的选择,即所有“攻击点”直接向汇点连边,流量为(1)费用为(0)
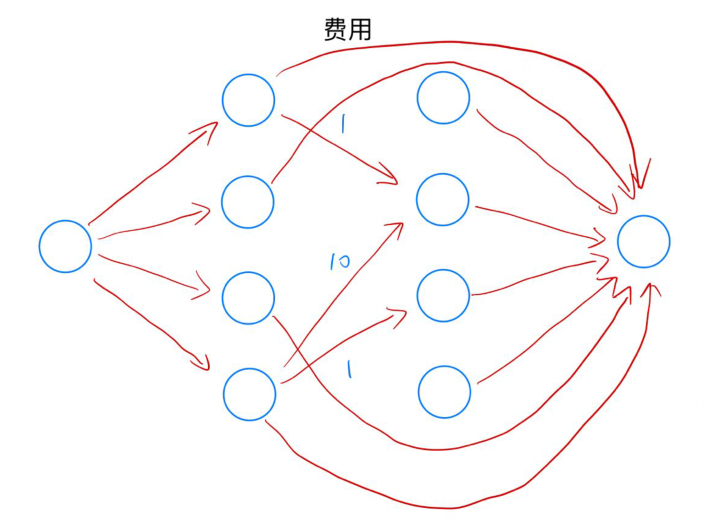
而由于边权取反,对于最小费用最大流而言,还是会取到这条费用为(-10)的边,本题结束,最终获得的费用再取反输出即可
来源
The 5th Guangting Cup Central China Invitational Programming Contest
代码
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=205;
struct MCMF {
struct E {
int from, to, cap, v;
E() {}
E(int f, int t, int cap, int v) : from(f), to(t), cap(cap), v(v) {}
};
int n, m, s, t;
vector<E> edges;
vector<int> G[maxn];
bool inq[maxn];
int dis[maxn], pre[maxn], a[maxn];
void init(int _n, int _s, int _t) {
n = _n; s = _s; t = _t;
for (int i = 0; i <= n; i++)
G[i].clear();
edges.clear();
m = 0;
}
void add(int from, int to, int cap, int cost) {
edges.emplace_back(from, to, cap, cost);
edges.emplace_back(to, from, 0, -cost);
G[from].push_back(m++);
G[to].push_back(m++);
}
bool spfa() {
for (int i = 0; i <= n; i++) {
dis[i] = 1e9;
pre[i] = -1;
inq[i] = false;
}
dis[s] = 0, a[s] = 1e9, inq[s] = true;
queue<int> Q; Q.push(s);
while (!Q.empty()) {
int u = Q.front(); Q.pop();
inq[u] = false;
for (int& idx: G[u]) {
E& e = edges[idx];
if (e.cap && dis[e.to] > dis[u] + e.v) {
dis[e.to] = dis[u] + e.v;
pre[e.to] = idx;
a[e.to] = min(a[u], e.cap);
if (!inq[e.to]) {
inq[e.to] = true;
Q.push(e.to);
}
}
}
}
return pre[t] != -1;
}
int solve() {
int flow = 0, cost = 0;
while (spfa()) {
flow += a[t];
cost += a[t] * dis[t];
int u = t;
while (u != s) {
edges[pre[u]].cap -= a[t];
edges[pre[u] ^ 1].cap += a[t];
u = edges[pre[u]].from;
}
}
return cost;
}
}f;
int v[maxn];
char str[maxn];
int main()
{
int n;
while(scanf("%d",&n)!=EOF&&n)
{
f.init(n*2+2,n*2+1,n*2+2);
for(int i=1;i<=n;i++)
scanf("%d",&v[i]);
for(int i=1;i<=n;i++)
{
scanf("%s",str+1);
for(int j=1;j<=n;j++)
if(str[j]=='1')
f.add(i,j+n,1,-(v[i]^v[j]));
}
for(int i=1;i<=n;i++)
{
f.add(f.s,i,1,0);
f.add(i,f.t,1,0);
f.add(i+n,f.t,1,0);
}
printf("%d
",-f.solve());
}
return 0;
}