深度学习中的线性代数知识详解

原创

深度学习中的概率知识详解

本文链接：https://blog.csdn.net/xialeizhou/article/details/81026315

1. 基础概念

随机变量(连续,离散): 对可能状态的描述, 在机器学习算法中，每个样本的特征取值，标签值都可以看作是一个随机变量，包括离散型随机变量和连续型随机变量
概率分布: 用来指定每个状态的可能性, 对于离散型的概率分布，称为概率质量函数(Probability Mass Function, PMF)，对于连续性的变量，其概率分布叫做概率密度函数(Probability Density Function, PDF).
边缘概率分布:如果我们知道了一组变量的联合概率分布,但想要了解其中一个子集的概率分布,这个子集的概率分布称为边缘概率分布
联合概率分布:两个或两个以上随机随机变量联合地概率分布情况。
相互独立: 如果 $\forall x \in X, y \in Y, P (X = x, Y = y) = P (X = x) P (Y = y)$ ，那么就称随机变量Ｘ和Ｙ是相互独立的。
条件独立: 如果 $\forall x \in X, y \in Y, z \in Z, P (X = x, Y = y ‖ Z = z) = P (X = x ‖ Z = z) P (Y = y ‖ Z = z)$ ，那么就称随机变量Ｘ和Ｙ是关于Ｚ相互独立的。
贝叶斯准则: 在已知 $P (y ‖ x)$ 和 $P (x)$ 的情况下， $P (x ‖ y) ＝ \frac{P (x) P (y ‖ x)}{P (y)}$ ，贝叶斯准则经常被用在已知参数的先验分布情况下求后验分布。
期望: 函数 $f (x)$ 在某个分布 $P (x)$ 下的平均表现情况，记为 $E_{x \sim P} [f (x)] = \int p (x) f (x) d x$ 。
方差: 函数 $f (x)$ 在某个分不下表现的差异性，记为 $V a r (f (x) = E [(f (x) - E [f (x)])^{2}]$ 。
协方差: 两个变量之间线性相关的强度，记为 $C o v (f (x), g (x)) = E [(f (x) - E [f (x)]) (g (x) - E (g (x)))]$ 。
条件概率: 求B条件下, A发生的概率:

P (A | B) = P ( A B ) P ( B )

条件概率的链式法则:

P (a, b, c) P (b, c) P (a, b, c) = P (a | b | c) P (b, c) = P (b | c) P (c) = P (a | b, c) P (b | c) P (c)

信息熵: 描述某个概率分布中不确定性的度量，记为

H (x) = - E_{x \sim P} [\log P (x)]

。
交叉熵: 描述两个概率分布之间相似度的一个指标，在机器学习中经常使用交叉熵作为分类任务的损失函数，记为

H (P, Q) = - E_{x \sim P} [\log Q (x)]

。

2. 期望,方差,协方差

期望反应函数 $f (x)$ 的平均值. 设 $E_{x} p [f (x)]$ 是函数 $f (x)$ 关于某分布 $P (x)$ 的期望:

对于离散型随机变量:
$E x p [f (x)] = \sum x P (x) f (x)$
对于连续性随机变量:

$E x p [f (x)] = \int p (x) f (x) d x$

通常在概率上下文中可以不写脚标: $E [f (x)]$ , 更一般地, 当没有歧义时可以省略方括号, 将期望简写为 $E$ .

期望是线性的:

E x [α f (x) + β g (x)] = α E x [f (x)] + β E x [g (x)]

方差衡量x依它的概率分布采样时, 随机变量x的函数 $f (x)$ 差异程度. 方差的定义:

V a r (f (x)) = E [| f (x) - E [f (x)] | 2]

协方差给出两个变量的线性相关度及这些变量的尺度. 协方差定义:

C o v (f (x), g (y)) = E [(f (x) - E [f (x)]) (g (y) - E (g (y)])]

3. 常用的概率分布模型

Bernoulli分布和Multinoulli分布

Bernoulli分布是单个二值随机变量分布, 单参数 $ϕ \in [0, 1]$ 控制, $ϕ$ 给出随机变量等于1的概率. 一些性质:
概率:

P (x = 1) P (x = 0) P (x = x) = ϕ = 1 - ϕ = ϕ x (1 - ϕ) 1 - x

方差,期望:

E x [x] V a r x (x) = ϕ = ϕ (1 - ϕ)

Multinoulli分布也叫范畴分布, 是单个 $k$ 值随机分布,经常用来表示对象分类的分布.
, 其中 $k$ 是有限值.Multinoulli分布由向量 $\vec{p} \in [0, 1]^{k - 1}$ 参数化,每个分量 $p_{i}$ 表示第i个状态的概率, 且 $p_{k} = 1 - 1^{T} p$ .

适用范围: 伯努利分布适合对离散型随机变量建模, 注意下述狄拉克 $δ$ 函数适用对连续性随机变量的经验分布建模.

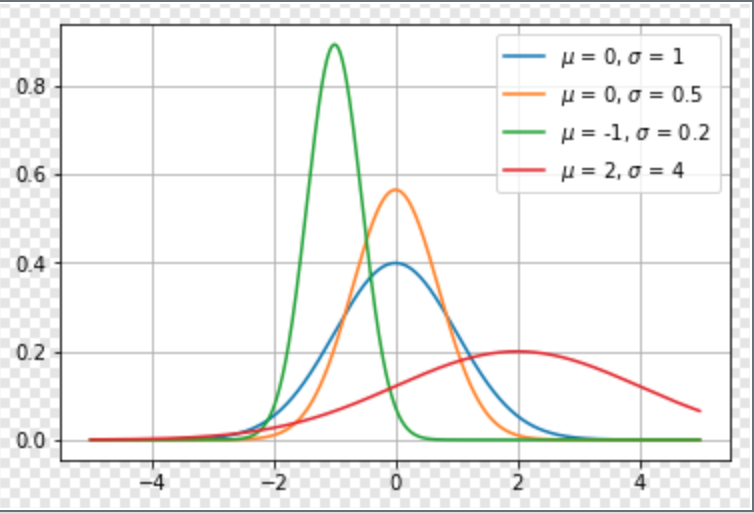
高斯分布

高斯也叫正态分布(Normal Distribution), 概率度函数如下:

N (x; μ, σ 2) = 1 2 π σ 2 - - - - - \sqrt e x p (- 1 2 σ 2 (x - μ) 2)

其中,

μ

和

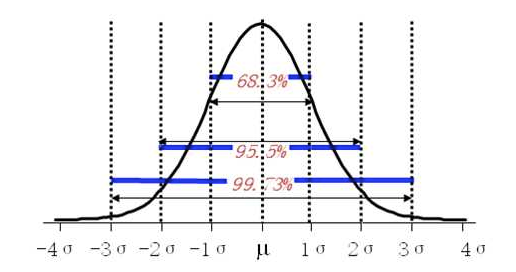
σ

分别是均值和方差, 中心峰值x坐标由

μ

给出, 峰的宽度受

σ

控制, 最大点在

x = μ

处取得, 拐点为

x = μ \pm σ

正态分布中，±1σ、±2σ、±3σ下的概率分别是68.3%、95.5%、99.73%，这3个数最好记住。
此外, 令 $μ = 0, σ = 1$ 高斯分布即简化为标准正态分布:

N (x; μ, σ 2) = 1 2 π - - - \sqrt e x p (- 1 2 x 2)

对概率密度函数高效求值:

N (x; μ, β - 1) = β 2 π - - - \sqrt e x p (- 1 2 β (x - μ) 2)

其中,

β = \frac{1}{σ^{2}}

, 通过参数

β \in (0, \infty)

来控制分布的精度.

问: 何时采用正态分布?
答: 缺乏实数上分布的先验知识, 不知选择何种形式时, 默认选择正态分布总是不会错的, 理由如下:
1. 中心极限定理告诉我们, 很多独立随机变量均近似服从正态分布, 现实中很多复杂系统都可以被建模成正态分布的噪声, 即使该系统可以被结构化分解.
2. 正态分布是具有相同方差的所有概率分布中, 不确定性最大的分布, 换句话说, 正态分布是对模型加入先验知识最少的分布.

正态分布的推广:
正态分布可以推广到 $R^{n}$ 空间, 此时称为多位正态分布, 其参数是一个正定对称矩阵 $\sum$ :

N (x; μ ⃗, \sum) = 1 2 π n d e t ( \sum ) - - - - - - - - - - \sqrt e x p (- 1 2 (x ⃗ - μ ⃗) T \sum - 1 (x ⃗ - μ ⃗))

对多为正态分布概率密度高效求值:

N (x; μ ⃗, β ⃗ - 1) = d e t (β ⃗) - - - - - \sqrt (2 π) n e x p (- 1 2 (x ⃗ - μ ⃗) T β (x ⃗ - μ ⃗))

, 此处, $\vec{β}$ 是一个精度矩阵.

指数分布和Laplace分布

指数分布

深度学习中, 指数分布用来描述在 $x = 0$ 点出取得边界点的分布, 指数分布定义如下:

p (x; λ) = λ 1 x \geq 0 e x p (- λ x)

, 指数分布用指示函数

I_{x >= 0}

来使x取负值时的概率为零.

* Laplace分布*
Laplace分布允许我们在任意一点 $μ$ 处设置概率质量的峰值:

L a p l a c e (x; μ; γ) = 1 2 γ e x p (- | x - μ | γ)

Dirac分布和经验分布

Dirac分布
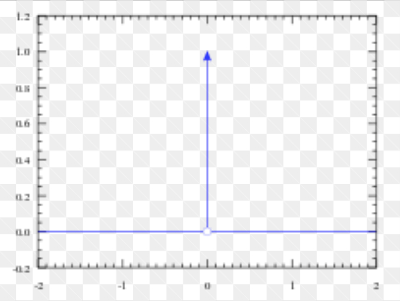
Dirac分布可保证概率分布中所有质量都集中在一个点上. Diract分布的狄拉克δ函数(也称为单位脉冲函数)定义如下:

p (x) = δ (x - μ), x \neq μ

\int b a δ (x - μ) d x = 1, a < μ < b

狄拉克δ函数图像:

狄拉克δ函数

说明:
- 严格来说狄拉克δ函数不能算是一个函数，而是一种数学对象, 因为满足以上条件的函数是不存在的, 但是我们可以用分布的概念来解释, 因此称为狄拉克分布或者 $δ$ 分布
- 它是一种极简单的广义函数. 广义函数是一种数学对象, 依据积分性质而定义. 我们可以把狄拉克 $δ$ 函数想成一系列函数的极限点, 这一系列函数把除0以外的所有点的概率密度越变越小.

经验分布
狄拉克分布常作为经验分布的一个组成部分:

p^(x ⃗) = 1 m \sum i = 1 m δ (x ⃗ - x ⃗ (i))

, 其中, m个点 $x^{(1)}$ , …, $x^{(m)}$ 是给定的数据集, 经验分布将概率密度 $\frac{1}{m}$ 赋给了这些点.

当我们在训练集上训练模型时, 可以认为从这个训练集上得到的经验分布指明了采样来源.

适用范围: 狄拉克δ函数适合对连续型随机变量的经验分布

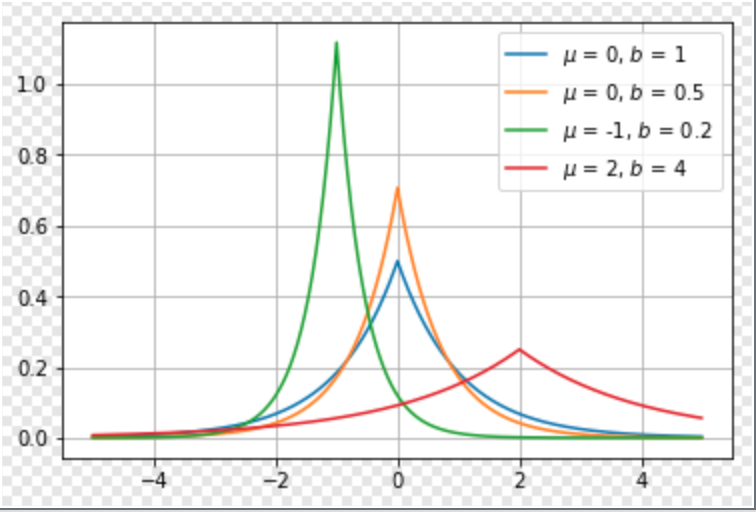
拉普拉斯分布(Laplace distribution)

有着与高斯分布很相近的形式，概率密度函数为Laplace(x;μ,γ)=12γexp(−|x−μ|γ)$，形状如下图：

高斯分布

拉普拉斯分布

4. 深度学习常用激活函数

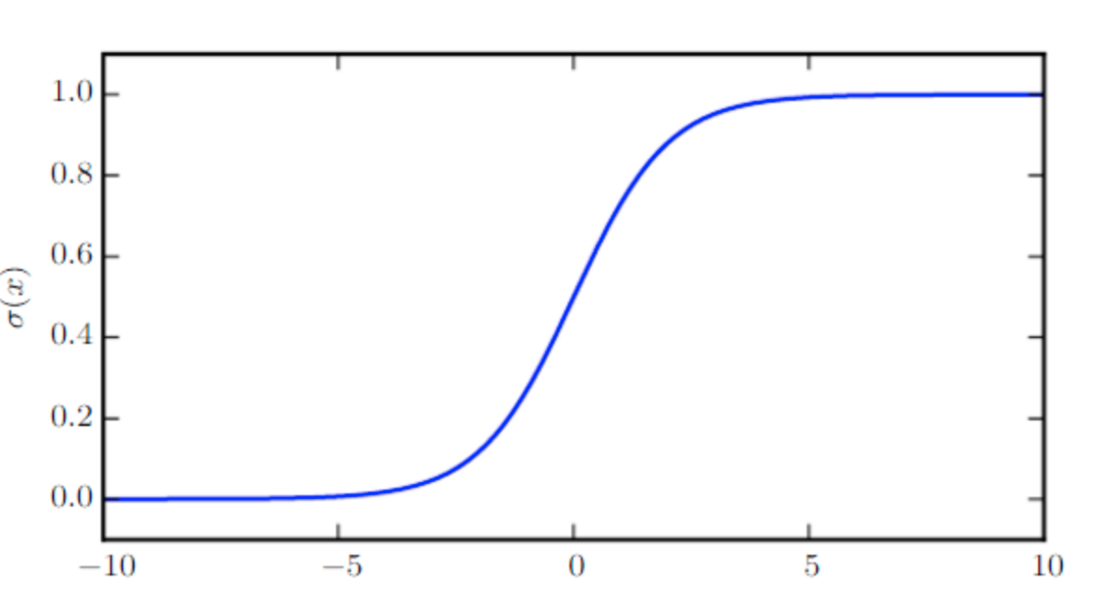
Logistic sigmoid函数
- $σ (x) = \frac{1}{1 + \exp (- x)}$
- 函数图像
- logistic函数有许多重要的性质，通常被用来对数值进行平滑，下面是它的部分性质
  
  $σ (x) d d x σ (x) 1 - σ (x) l o g σ (x) = e x e x + e 0 = σ (x) (1 - σ (x)) = σ (- x) = - ζ (- x)$
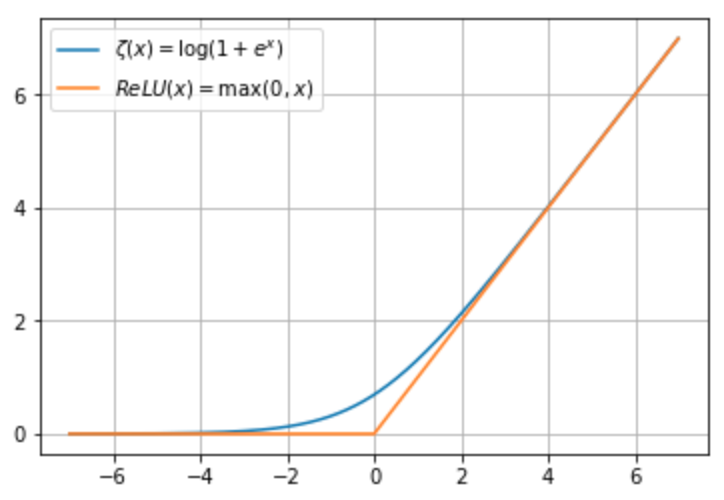
线性整流函数(Rectified Linear Unit, ReLU)
- $R e L U (x) = m a x (0, x)$
- 目前神经网络中最常用的一种非线性激活函数
Softplus函数
- $ζ (x) = \log (1 + \exp (x))$
- softplus函数可以看作是 $m a x (0, x)$ 的一个平滑，他与ReLU的函数图像如下
- 它有如下性质
  
  $d d x ξ (x) \forall x \in (0, 1), σ - 1 (x) \forall x > 0, ζ - 1 (x) ζ (x) ζ (x) - ζ (- x) = σ (x) = l o g (x 1 - x) = l o g (e x - 1) = \int x - \infty σ (y) d y = x$

5．结构化概率模型

概率图模型: 通过图的概念来表示随机变量之间的概率依赖关系
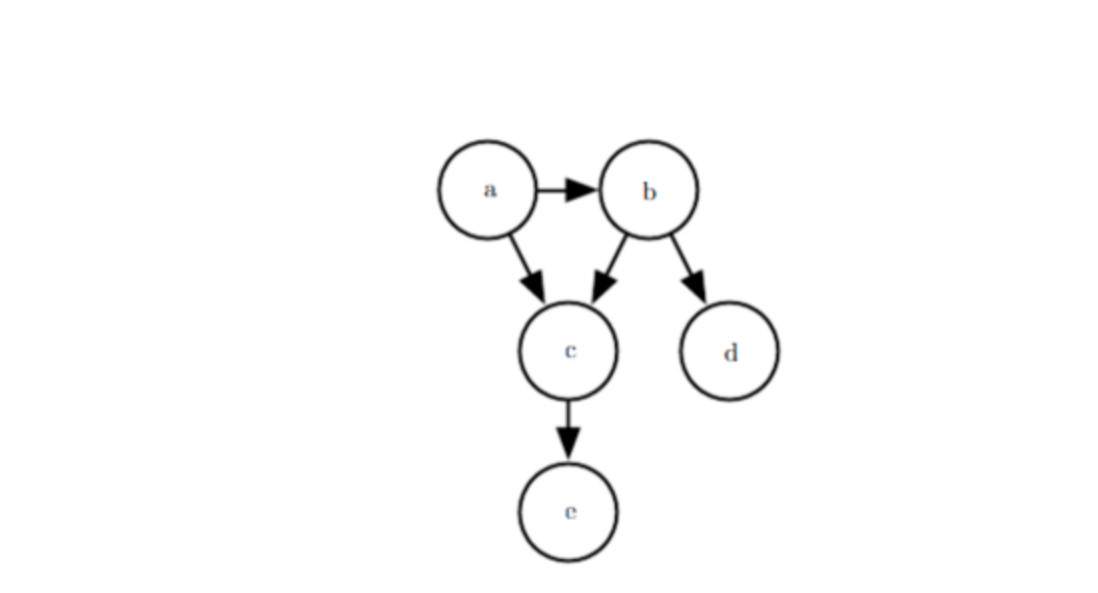
有向图表示的概率模型：

下图即为一个关于变量 $a, b, c, d, e$ 之间的有向图模型，通过该图可以计算

p (a, b, c, d, e) = p (a) p (b ∥ a) p (c ∥ a, b) p (d ∥ b) p (e ∥ c)

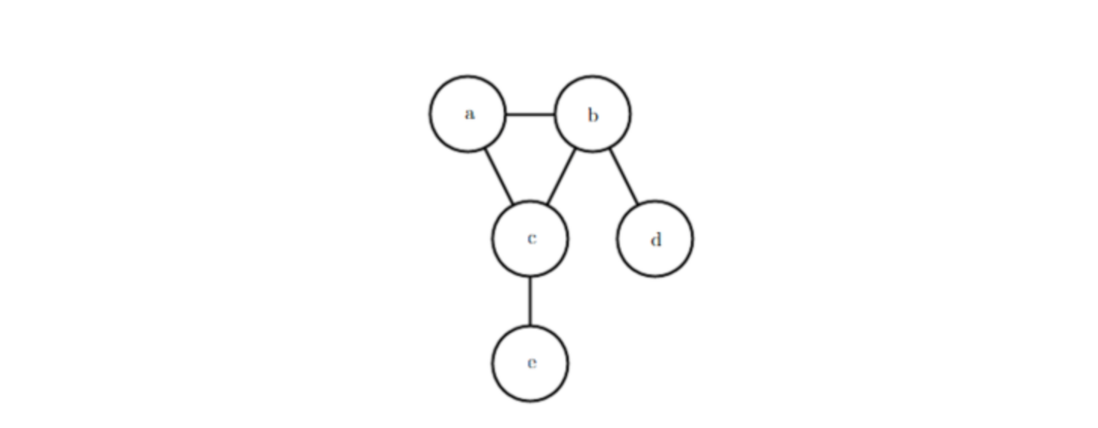
无向图表示的概率模型：
公式:

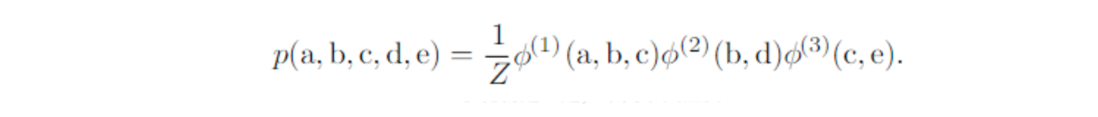
图:

似然函数

在数理统计学中，似然函数是一种关于统计模型中的参数的函数，表示模型参数中的似然性。似然函数可以理解为条件概率的逆反。

在已知某个参数 $α$ 时，事件A会发生的条件概率可以写作 $P (A; α)$ ，也就是 $P (A | α)$ 。我们也可以构造似然性的方法来表示事件A发生后估计参数 $α$ 的可能性，也就表示为 $L (α | A)$ ，其中 $L (α | A) = P (A | α)$ 。

最大似然估计（MLE）与最大后验概率（MAP）

最大似然估计是似然函数最初的应用。似然函数取得最大值表示相应的参数能够使得统计模型最为合理。从这样一个想法出发，最大似然估计的做法是：首先选取似然函数（一般是概率密度函数或概率质量函数），整理之后求最大值。实际应用中一般会取似然函数的对数作为求最大值的函数，这样求出的最大值和直接求最大值得到的结果是相同的。似然函数的最大值不一定唯一，也不一定存在。

这里简单的说一下最大后验概率（MAP），如下面的公式

P (α | X) = P ( X | α ) P ( α ) P ( X )

其中等式左边

P (α | X)

表示的就是后验概率，优化目标即为

a r g m a x_{α} P (α | X)

，即给定了观测值X以后使模型参数

α

出现的概率最大。等式右边的分子式

P (X | α)

即为似然函数

L (α | X)

，MAP考虑了模型参数

α

出现的先验概率

P (α)

。即就算似然概率

P (X | α)

很大，但是

α

出现的可能性很小，也更倾向于不考虑模型参数为

α

。

生成式模型与判别式模型

判别式模型学习的目标是条件概率 $P (Y | X)$ 或者是决策函数 $Y = f (X)$ ，其实这两者本质上是相同的。例如KNN，决策树，SVM，CRF等模型都是判别式模型。

生成模型学习的是联合概率分布 $P (X, Y)$ ，从而求得条件概率分布 $P (Y | X)$ 。例如NB，HMM等模型都是生成式模型。