LIS定义:
LIS(Longest Increasing Subsequence)最长上升子序列
一个数的序列bi,当b1 < b2 < … < bS的时候,我们称这个序列是上升的。
对于给定的一个序列(a1, a2, …, aN),我们可以得到一些上升的子序列(ai1, ai2, …, aiK),
这里1 <= i1 < i2 < … < iK <= N。
比如,对于序列(1,5,3,4,8),有它的一些上升子序列,如(1, 8), (3, 4, 8)等等。
这些子序列中最长的长度是4,比如子序列(1, 3, 4, 8).
你的任务,就是对于给定的序列,求出最长上升子序列的长度。
O(N^2)做法:dp动态规划:
状态设计:dp[i]代表以a[i]结尾的LIS的长度
状态转移:dp[i]=max(dp[i], dp[j]+1) (0<=j< i, a[j]< a[i])
边界处理:dp[i]=1 (0<=j< n)
时间复杂度:O(N^2)
举例:(1,5,3,4,8),先画个图:(红色的忽略。。。。)
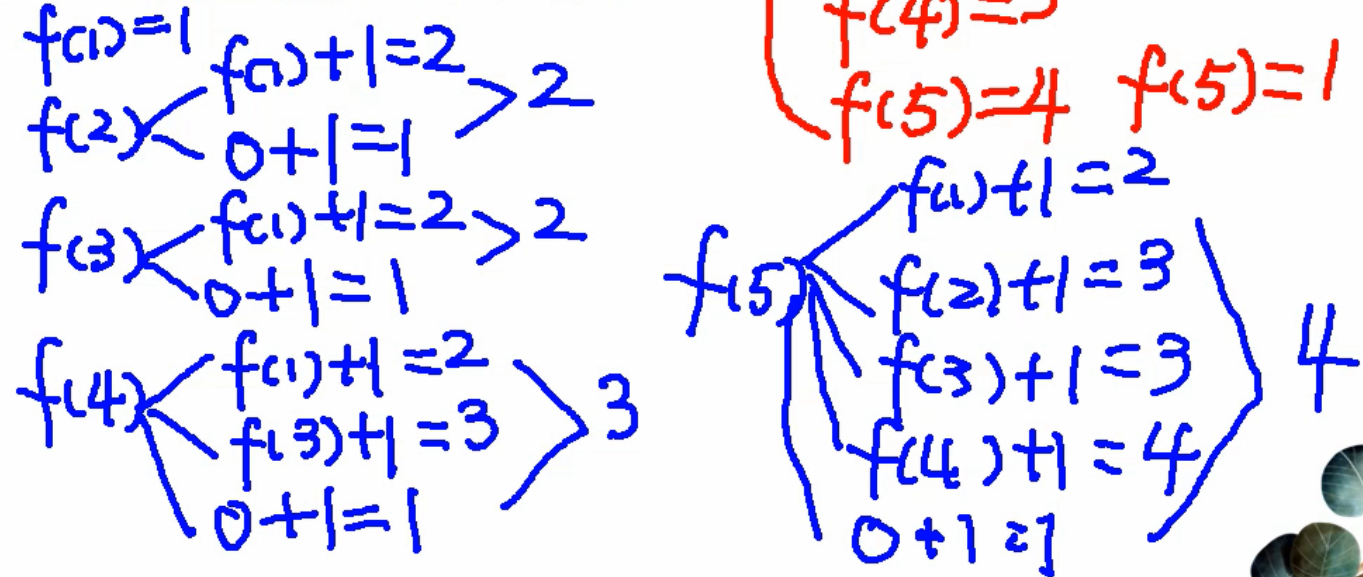
| dp[i] | 初始值 | j=1 | j=2 | j=3 | j=4 | j=5 |
| dp[1] | 1 | 1 | ||||
| dp[2] | 1 | 1 | 2 | |||
| dp[3] | 1 | 1 | 2 | 2 | ||
| dp[4] | 1 | 1 | 2 | 2 | 3 | |
| dp[5] | 1 | 1 | 2 | 2 | 3 | 4 |
注意:求完dp数组后,取其中的最大值就是LIS的长度。【注意答案不是dp[n],这个样例只是巧合】,例如如果最后一位是0的话dp[5]=1;

#include<stdio.h> #include<iostream> #include<string.h> #include<queue> #include<cstdio> #include<string> #include<math.h> #include<algorithm> #include<map> #include<set> #include<stack> #define mod 998244353 #define INF 0x3f3f3f3f #define eps 1e-6 using namespace std; typedef long long ll; using namespace std; const int MAXX=10000+5; int a[MAXX],dp[MAXX]; // a数组为数据,dp[i]表示以a[i]结尾的最长递增子序列长度 int n; int LIS(){ int ans=1; for(int i=1; i<=n; i++)//枚举子序列的终点 { dp[i]=1;// 初始化为1,长度最短为自身 for(int j=1; j<i; j++)//从头向终点检查每一个元素 { if(a[i]>a[j]) { dp[i]=max(dp[i],dp[j]+1); // 状态转移 } } ans=max(ans,dp[i]); // 比较每一个dp[i],最大值为答案 } return ans; } int main() { while(cin>>n) { for(int i=1; i<=n; i++) { cin>>a[i]; } int ans=LIS(); cout<<ans<<endl; } return 0; }
下面附上一个例题:
Codeforces Round #641 (Div. 2)
B. Orac and Models
There are nn models in the shop numbered from 11 to nn, with sizes s1,s2,…,sns1,s2,…,sn.
Orac will buy some of the models and will arrange them in the order of increasing numbers (i.e. indices, but not sizes).
Orac thinks that the obtained arrangement is beatiful, if for any two adjacent models with indices ijij and ij+1ij+1 (note that ij<ij+1ij<ij+1, because Orac arranged them properly), ij+1ij+1 is divisible by ijij and sij<sij+1sij<sij+1.
For example, for 66 models with sizes {3,6,7,7,7,7}{3,6,7,7,7,7}, he can buy models with indices 11, 22, and 66, and the obtained arrangement will be beautiful. Also, note that the arrangement with exactly one model is also considered beautiful.
Orac wants to know the maximum number of models that he can buy, and he may ask you these queries many times.
The first line contains one integer t (1≤t≤100)t (1≤t≤100): the number of queries.
Each query contains two lines. The first line contains one integer n (1≤n≤100000)n (1≤n≤100000): the number of models in the shop, and the second line contains nn integers s1,…,sn (1≤si≤109)s1,…,sn (1≤si≤109): the sizes of models.
It is guaranteed that the total sum of nn is at most 100000100000.
Print tt lines, the ii-th of them should contain the maximum number of models that Orac can buy for the ii-th query.
题意:这里求得也是最长上升子序列,不过变化了一点,就是后一个数在原序列对应的下标必须是前一个数在原序列的下标的倍数。
思路:既然求得是倍数递增子序列,就不能只是按照原来的套路了。需要把if哪里改变一下。
1 if(i%j==0) 2 { 3 if(a[i]>a[j]) 4 { 5 dp[i]=max(dp[i],dp[j]+1); 6 } 7 if(a[i]>a[i/j]) 8 { 9 dp[i]=max(dp[i],dp[i/j]+1); 10 } 11 }
第一行容易理解肯定是要判断他能否被j整除。然后判断一下大小就行了。但是问题来了,题目给的时间是3秒但是数据范围是1e5,用n^2的复杂度肯定会超时,所以加了个小优化,在第二层循环的时候开根号。
就变成了这个样子
1 for(int j=1; j<=sqrt(i)+1; j++)
但是这样会造成某些元素被忽略。比如当i是10的时候,10开根号大概是3点多,所以j的范围就是[1,3]了,忽略了5,但是5还能被整除啊,所以就加了一行这个
if(a[i]>a[i/j]) dp[i]=max(dp[i],dp[i/j]+1);
这样就可以全部考虑到了,当j是2 的时候,我用10/2=5;5就可以考虑到了。(也就是先找出来较小的除数,然后大的除数,用被除数除以较小的除数就行了)其他的也和这个类似,下面看代码:

#include<iostream> #include<string.h> #include<queue> #include<cstdio> #include<string> #include<math.h> #include<algorithm> #define mod 998244353 #define INF 0x3f3f3f3f using namespace std; typedef long long ll; using namespace std; const int MAXX=100000+5; int a[MAXX],dp[MAXX]; int n; int LIS() { int ans=1; for(int i=1; i<=n; i++) { dp[i]=1; for(int j=1; j<=sqrt(i); j++) { if(i%j==0&&j!=i) { if(a[i]>a[j]) { dp[i]=max(dp[i],dp[j]+1); } if(a[i]>a[i/j]) { dp[i]=max(dp[i],dp[i/j]+1); } } } ans=max(ans,dp[i]); } return ans; } int main() { int t; cin>>t; while(t--) { cin>>n; for(int i=1; i<=n; i++) { cin>>a[i]; } int ans=LIS(); cout<<ans<<endl; } return 0; }
l
