矩阵快速幂
顾名思义,矩阵快速幂可以简单理解为在矩阵上实现快速幂操作并且达到一定的目的。
但是,矩阵快速幂很抽象,本文将分为以下部分进行介绍:
1.矩阵乘法(了解矩阵乘法的可以跳过)
2.引入及算法实现
3.应用
1.矩阵乘法
我们定义一个有 M * N 个数排列的 M 行 N 列的矩阵 , 简称 M * N 的矩阵
e.g.一个 2 * 3 的矩阵
1 3 3
2 1 8
对于矩阵加法,只能是两个大小相同的矩阵相加(及 M = M· && N = N·)
这个很好理解,但对于矩阵乘法,就相对复杂。
矩阵乘法只适用于 第一个矩阵的 列数 和 第二个矩阵的 行数 相等时,才能相乘。
如: A矩阵 2 行 3 列 , B 矩阵 3 行 2 列 ,答案矩阵 2 行 2 列 。
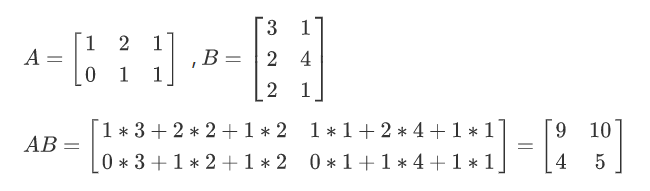
简单来说,既是 C 矩阵的行数由 A 矩阵行数决定 , C 矩阵的列数由 B 矩阵列数决定。
C中每一个值运算方法如下:
C中第 i 行 j 列 元素 = ( k 属于 1 ~ A的列数 ) A中第 i 行 k 列 元素 * B中第 k 行 j 列 元素 之和。
有一种特殊的矩阵:单位矩阵,它从左上角到右下角的对角线上的元素均为1,除此以外全都为0。它在矩阵乘中相当于数乘中的1,即任何矩阵乘它都等于本身。
顺便提一下,矩阵乘法满足结合律,分配律,但不满足交换律(定义条件不符合)
2.引入及算法实现
至于为什么要使用矩阵快速幂,下面给出例题。
E.G.
斐波拉契数列定义: F[ i ] = F[ i - 1 ] + F[ i - 2 ] ( i >= 3 )
F[ 1 ] = 1 , F[ 2 ] = 1 ;
out: F[ n ] % 10007 ( n <= 10000 )
初看非常简单,递推即可。
但是,如果 n <= 2 000 000 呢?
如果简单递推,显然会超时。
但是我们发现 第 n 项仅有 第 n - 1 和 n - 2 项递推来,如何快速计算中间的冗杂步骤,是最重要的。
如果尝试用矩阵快速幂呢?
由于要使其可以线性递推,我们首先要构造 一个初始矩阵 S , 一个目标矩阵 A , 和一个过渡矩阵 T 。
s = | F[ i - 1 ] | A = | F[ i ] |
| F[ i - 2 ] | | F[ i - 1 ] |
考虑如何从 S 过渡到 A , 我们需要构造一个过渡矩阵 T(通常放在 a1*a2=a3 中 a1 的位置 ) 。
回来看定义 F[ i ] = F[ i - 1 ] + F[ i - 2 ]
根据矩阵乘法的定义及性质,得到 T 矩阵:
T = | 1 , 1 | // F[ i ] = F[ i - 1 ] * 1 + F[ i - 2 ] * 1
| 1 , 0 | // F[ i - 1 ] = F[ i - 1 ] * 1
由于满足矩阵乘法的性质,可以在矩阵上使用快速幂来达到降低时间复杂度的目的。及如下:
Fi = Ti * F0
给出代码和详细过程
#include<bits/stdc++.h>
#define mod 1000000007
#define ll long long
using namespace std;
struct Mat{
ll m[3][3];
}T,e;//T是 过渡矩阵,e是单位矩阵
ll p;
Mat Matrix(Mat x,Mat y) //矩阵乘
{
Mat c;
for( int i = 1 ; i <= 2 ; i++ )
for( int j = 1 ; j <= 2 ; j++ )
c.m[ i ][ j ] = 0 ;//你可以试试不初始化的后果(推荐考试尝试)
for( int i = 1 ; i <= 2 ; i++ )
for( int j = 1 ; j <= 2 ; j++ )
for( int k = 1 ; k <= 2 ; k++ )//矩阵乘法原则
c.m[ i ][ j ] = ( c.m[ i ][ j ] + x.m[ i ][ k ] * y.m[ k ][ j ] % mod )%mod;
return c;
}
Mat fast_Matrix( Mat res , ll y ) //快速幂
{
Mat ans = e ;// 单位矩阵 就像 普通快速幂 的初始 res = 1 一样
while( y ) {
if( y & 1 )
ans = Matrix( ans , res );
res = Matrix( res , res );
y>>=1;
}
return ans;
}
int main()
{
cin>>p;
if( p <= 2 ){ printf("1") ; return 0 ; }//特判一下
T.m[ 1 ][ 1 ] = T.m[ 1 ][ 2 ] = T.m[ 2 ][ 1 ] = 1 ; //过渡矩阵
e.m[ 1 ][ 1 ] = e.m[ 2 ][ 2 ] = 1 ;//单位矩阵
Mat ans = fast_Matrix( T , p - 2 );//矩阵快速幂
ll tot = ( ans.m[1][1]*1 + ans.m[1][2]*1 ) % mod; //处理出答案
cout<<tot<<" ";
return 0;
}
好了到这里,相信你应该对矩阵快速幂有了一定的掌握,如果担心写错,可以和递推的斐波拉契写下对拍,问题不本质。
3.应用
写了上面一道题,对于以下这道应该没问题,只是改一下参数,但是过渡矩阵还是要自己推,练下手。
题目:洛谷【模板】矩阵加速(数列)
已知
a[1]=a[2]=a[3]=1
a[x]=a[x-3]+a[x-1] (x>3)
求a数列的第n项对1000000007(10^9+7)取余的值。
改下参数,建立矩阵,完了,AC代码和上面几乎一模一样。
#include<bits/stdc++.h>
#define mod 1000000007
#define ll long long
using namespace std;
struct Mat{
ll m[5][5];
}T,e;//T是 过渡矩阵,e是单位矩阵
ll p;
Mat Matrix(Mat x,Mat y) //矩阵乘
{
Mat c;
for( int i = 1 ; i <= 3 ; i++ )
for( int j = 1 ; j <= 3 ; j++ )
c.m[ i ][ j ] = 0 ;
for( int i = 1 ; i <= 3 ; i++ )
for( int j = 1 ; j <= 3 ; j++ )
for( int k = 1 ; k <= 3 ; k++ )//矩阵乘法原则
c.m[ i ][ j ] = ( c.m[ i ][ j ] + x.m[ i ][ k ] * y.m[ k ][ j ] % mod )%mod;
return c;
}
Mat fast_Matrix( Mat res , ll y ) //快速幂
{
Mat ans = e ;
while( y ) {
if( y & 1 )
ans = Matrix( ans , res );
res = Matrix( res , res );
y>>=1;
}
return ans;
}
int main()
{
int times ;
cin>>times;
while( times--){
cin>>p;
if( p <= 3 ){ printf("1
") ; continue ; }
T.m[ 1 ][ 1 ] = T.m[ 1 ][ 3 ] = T.m[ 2 ][ 1 ] = T.m[ 3 ][ 2 ] = 1 ;
e.m[ 1 ][ 1 ] = e.m[ 2 ][ 2 ] = e.m[ 3 ][ 3 ] = 1 ;//单位矩阵
Mat ans = fast_Matrix( T , p - 3 );//矩阵快速幂
ll tot = ( ans.m[1][1]*1 + ans.m[1][2]*1 + ans.m[1][3]*1 ) % mod; //处理出答案
cout<<tot<<endl;
}
return 0;
}
那我们最后再来一道

本题除了构造矩阵外,还要考虑相乘爆 long long 的情况,代码暂不给出。