1.思维导图

2.重要概念的笔记
一.图的分类
1.图:是由一个顶点集 V 和一个顶点间的关系集合组成的数据结构。
2.无向图: 图中顶点之间的边都是无向边。如果任意两个顶点之间都存在边,则称该图为无向完全图,含有n个顶点的无向完全图有n(n-1)/2条边。
3.有向图: 图中顶点之间的边都是有向边。如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。含有n个顶点的有向完全图有n(n-1)条边。
5.稀疏图、稠密图:边或弧的个数 e<nlogn为稀疏图,否则为稠密图。
5.连通图: 在无向图中,对于图中任意两个顶点都是连通的(顶点i到顶点j有路径).
6.强连通图: 在有向图中,对于图中任意两个顶点都是连通的。
二.图的基本概念
1.度:顶点v关联的边的数目定义为边的度。对于有向图,顶点的度=顶点的入度+顶点的出度。无向图中所有顶点的度之和等于边数的2倍,有向图中所有顶点的入度之和等于所有顶点的出度之和。
2.简单路径:序列中顶点不重复出现的路径称为简单路径。
3.简单回路:除了第一个顶点和最后一个顶点之外,其余顶点不重复出现的回路,序列中第一个顶点和最后一个顶点相同的路径,称为简单回路或简单环。
4.连通图:若图G中任意两个顶点之间都有路径相通,则称此图为连通图;
5.连通分量:若无向图为非连通图,则图中各个极大连通子图称作此图的连通分量。
三.图的代码实现
图的邻接矩阵
#define MAXVEXNUM 最大顶点个数
typedef int ArcCell;
typedef char VexType;
typedef struct {
VexType vexs[MAXVEXNUM];//点的集合
ArcCell arcs[MAXVEXNUM][MAXVEXNUM];//边的集合
int vexNum, arcNum;
}MyGraph;
图的邻接表
typedef struct ArcNode
{
int adjvex;
int weight;
struct ArcNode* nextarc;
}ArcNode;
typedef struct VNode
{
VerTexType data;
ArcNode* firstarc;
}VNode;
typedef struct
{
int n, e;
VNode adjlist[MAXV];
}Adjraph;
图的邻接矩阵的建立
void CreateGraphFromConsole(MyGraph& G, int vexNum, int arcNum)
{
G.vexNum = vexNum;
G.arcNum = arcNum;
//初始化
for (int i = 0; i < vexNum; i++)
{
G.visited[i] = 0;
for (int j = 0; j < vexNum; j++)
{
G.arcs[i][j] = 0;
}
}
printf("Please input %d vex name:
", vexNum);
//cout << "输入点信息" << endl;
//点
for (int i = 0; i < vexNum; i++)
{
printf("i=%d ", i);
cin >> G.vexs[i];
}
//边
for (int j = 0; j < arcNum; j++)
{
char a, b;
ArcCell c;
cout << "输入x点,y点,及x到y边的值:" << endl;
cin >> a >> b >> c;
cout << " x=" << a << "," << " y=" << b << "," << " value=" << c << endl;
G.arcs[LocateVex(G, a)][LocateVex(G, b)] = c;
G.arcs[LocateVex(G, b)][LocateVex(G, a)] = c;
}
}
int LocateVex(MyGraph& G, VexType value)
{
for (int i = 0; i < G.vexNum; i++)
{
if (value == G.vexs[i])
return i;
}
return -1;
}
图的深度遍历DFS
void DFSTravse(MyGraph& G, int v) //深度遍历
{
int i;
cout << G.vexs[v] << " ";
G.visited[v] = 1;
for (i = 0; i < G.vexNum; i++)
{
if (G.arcs[v][i]) {
if (G.visited[i] == 0)
DFSTravse(G, i);
}
}
}
图的广度遍历BFS
void BFSTravse(MyGraph& G, int v) //广度遍历
{
queue<int>q;
G.visited[v] = 1;
q.push(v);
while (!q.empty())
{
int k = q.front();
q.pop();
cout << G.vexs[k] << " ";
for (int i = 0; i < G.vexNum; i++)
{
if (G.arcs[k][i] != 0 && G.visited[i] == 0){
q.push(i);
G.visited[i] = 1;
}
}
}
}
四.最小生成树
概念
包含无向连通图G所有n个顶点的极小连通子图称为G的生成树,其中权值之和最小的生成树为最小生成树
1.普利姆(Prim)算法
时间复杂度:O(n2),适用于稠密图
基本思想:
第一步:取图中任意一个顶点 v 作为生成树的根;
第二步:往生成树上添加新的顶点 w。在添加的顶点w 和已经在生成树上的顶点v 之间必定存在一条边,并且该边的权值在所有连通顶点 v 和 w 之间的边中取值最小;
第三步:继续往生成树上添加顶点,直至生成树上含有 n 个顶点为止。
2.克鲁斯卡尔(Kruskal)算法
在剩下的所有未选取的边中,找最小边,如果和已选取的边构成回路,则放弃,选取次小边。
时间复杂度:O(eloge),适用于稀疏图
基本思想:
第一步:构造一个只含 n 个顶点的子图 SG;
第二步:从权值最小的边开始,若它的添加不使SG中产生回路,则在 SG 上加上这条边;
第三步:如此重复,直至加上 n-1 条边为止。
五.最短路径
1.迪杰斯特拉(Dijkstra)算法:
按路径长度递增次序产生最短路径算法,时间复杂度为O(n3)。
•把V分成两组
•⑴S:已求出最短路径的顶点的集合
•⑵T=V-S:尚未确定最短路径的顶点集合
•将T中顶点按最短路径递增的次序加入到S中,直到T中没有顶点为止。
2.弗洛伊德(Floyd)算法
逐个顶点试探,时间复杂度为O(n3)。
从vi到vj的所有可能存在的路径中,选出一条长度最短的路径。
•初始设置一个n阶方阵,令其对角线元素为0,若存在弧<vi,vj>,则对应元素为权值,否则为无穷。
•逐步试着在原直接路径中增加中间顶点,若加入中间点后路径变短,则修改。否则,维持原值。
•所有顶点试探完毕,算法结束。
六.拓扑排序
拓扑排序的有向图中没有回路。
AOV-网中不应该出现有向环。
一个AOV-网的拓扑序列不是唯一的。
拓扑排序:
•从有向图中选取一个没有前驱的顶点,并输出之;
•从有向图中删去此顶点以及所有以它为尾的弧;
•重复上述两步,直至图空,或者图不空但找不到无前驱的顶点为止。
七.关键路径
概念:
•事件vi的最早发生时间:从开始点v1到vi的最长路径长度。用ve(i)表示.
•事件vi的最迟发生时间:在不推迟整个工期的前提下,事件vi允许的最晚发生时间。用vl(i)表示。
•活动ai的最早开始时间:即为ai的弧尾顶点(事件)的最早发生时间。用e(i)表示。
•活动ai的最迟开始时间:在保证不推迟整个工程的完成时间的前提下,活动ai的最迟开始时间。用l(i)表示。
•关键活动:l(i) = e(i)的活动。
算法实现
•输入e条弧,建立AOE-网。
•从源点v0出发,令ve[0] = 0, 按拓扑有序求各顶点的最早发生时间vei,如果得到的拓扑序列中顶点个数小于网中顶点数n,说明网中存在环,不能求关键路径,算法终止;否则执行步骤。
•从汇点vn出发,令vl[n-1] = ve[n-1]; 按逆拓扑有序求其余各顶点的最迟发生时间vli。
•根据各个顶点的ve和vl值,求每条弧s的e(s)和l(s)。若某条弧满足e(s) == l(s),则为关键活动。
3.疑难问题及解决方案

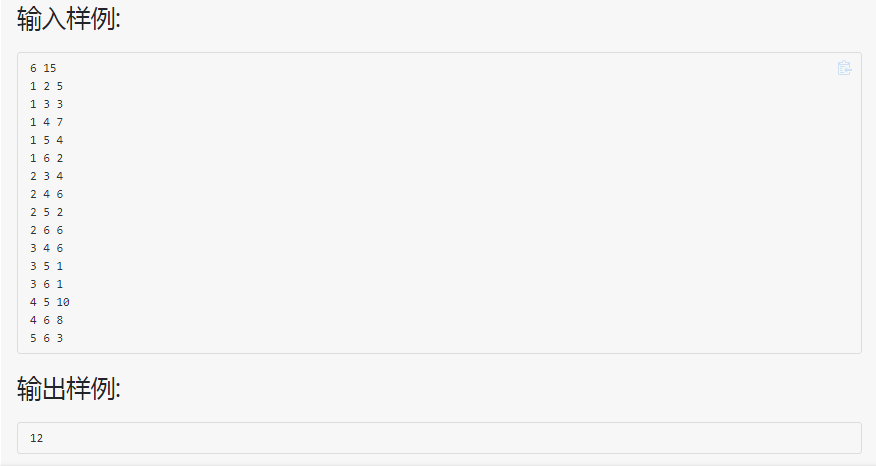
这道题的意思就是根据数据创建出一个图,如果图不能连通则输出-1,若可以连通则输出最小生成树的权值之和,最开始会发生一些小意外,一些细节的地方没处理好,比如题目要求的最多的城镇数目小于1000,最初没注意这个导致运行结果最后几个点运行超时,用define设置了最大顶点数后又发现没有错误但运行失败,比对了同学的代码才发现我未对邻接矩阵申请空间导致运行失败,且优化了对检测图是否连通的代码,对一些细节也进行了优化
#include<iostream>
using namespace std;
#define MAXV 2000 //最大顶点数
#define INF 32767 //表示∞
typedef struct
{
int n, e;
int arcs[MAXV][MAXV];
}MGraph;
void CreateGraphFromConsole(MGraph* G, int n, int e);
void prim(MGraph* G, int v);
int main()
{
int N, M;
cin >> N >> M;
MGraph* G = new MGraph;
CreateGraphFromConsole(G, N, M);
if (M < (N - 1))
cout << "-1";
else
prim(G, 1);
return 0;
}
void CreateGraphFromConsole(MGraph* G, int n, int e)
{
int i, j, x, y, w;
G->n = n;
G->e = e;
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
G->arcs[i][j] = INF;
for (i = 1; i <= e; i++)
{
cin >> x >> y >> w;
G->arcs[x][y] = G->arcs[y][x] = w;
}
}
void prim(MGraph* G, int v)
{
int i, j, l, k, sum = 0, min;
int lowcost[MAXV] = { 0 }, closedge[MAXV] = { 0 };
for (i = 2; i <= G->n; i++)
{
closedge[i] = v;
lowcost[i] = G->arcs[v][i];
}
for (i = 2; i <= G->n; i++)
{
min = INF;
for (j = 2; j <= G->n; j++) {
if (lowcost[j] != 0 && lowcost[j] < min) {
min = lowcost[j];
k = j;
}
}
sum += min;
lowcost[k] = 0;
for (l = 2; l < G->n; l++) {
if (lowcost[l] != 0 && lowcost[l] > G->arcs[k][l])
{
lowcost[l] = G->arcs[k][l];
closedge[l] = k;
}
}
}
int flag = 0;
for (i = 2; i <= G->n; i++) {
if (lowcost[i])
{
flag = 1;
break;
}
}
if (flag)
cout << "-1";
else
cout << sum;
}