一道计数题
一道华东师范大学出的NOI模拟题
一个1-N的排列p,定义(q_i)表示满足(j<i,p_j<p_i)的最大的j,如果不存在就为0.
现给出q序列,问有多少种可能的排列,答案对998244353取模。
一道挺神仙的题。
尝试手动模拟数据,发现在排列中1对应的q一定是q中最后一个0。例如
p 3 5 1 4 2
q 0 1 0 3 3
为什么?模拟求q的过程。假定我们不从左到右求q,而是根据排列中1-N的顺序求q。假设我们一个一个往序列中添加数字:
- 1的q一定是0,因为没有比1小的数。
- 对2而言它前面有一个1(此时4尚未被添加),因此q为3;
- 对3而言它前面没有数,因此q为0;
- 对4而言它前面有一个1,q为3;
- 对5而言它前面有一个3,q为1
上述过程说明了什么?在1后面的q一定非0(因为前面有这个1),因此1对应的q是q中最后一个0。推而广之,以(p_3=1)为分界,容易发现(p_{1sim 2})的q是大于等于0的(废话),而(p_{4sim 5})的q是大于等于3的,因为前面有一个1。于是我们可以说,在(p_{4sim 5})中的最小数字对应的q一定是(q_{4sim 5})中最后一个3,例如数据中的(p_5=2)。
于是我们说得再抽象一点,对于排列p及其对应的q,可以推出
- p中的最小数字(p_{x})(即1),那么(q_x)一定是q中最后一个0;
- (p_{1sim x-1})中的最小数字(p_y),那么(q_y)一定是(p_{1sim x-1})中最后一个0(因为(p_y)前面没有比它小的数);
- (p_{x+1sim n})中的最小数字(p_z),那么(q_z)一定是(p_{x+1sim n})中最后一个(q_x),即(q_z=q_x),因为(p_{x+1sim n})没有比(p_z)小的数,离它最近的是(p_x).
这就是一个递归的模型啊。于是可以按照这个模型建一棵树,显然这是一棵二叉树。
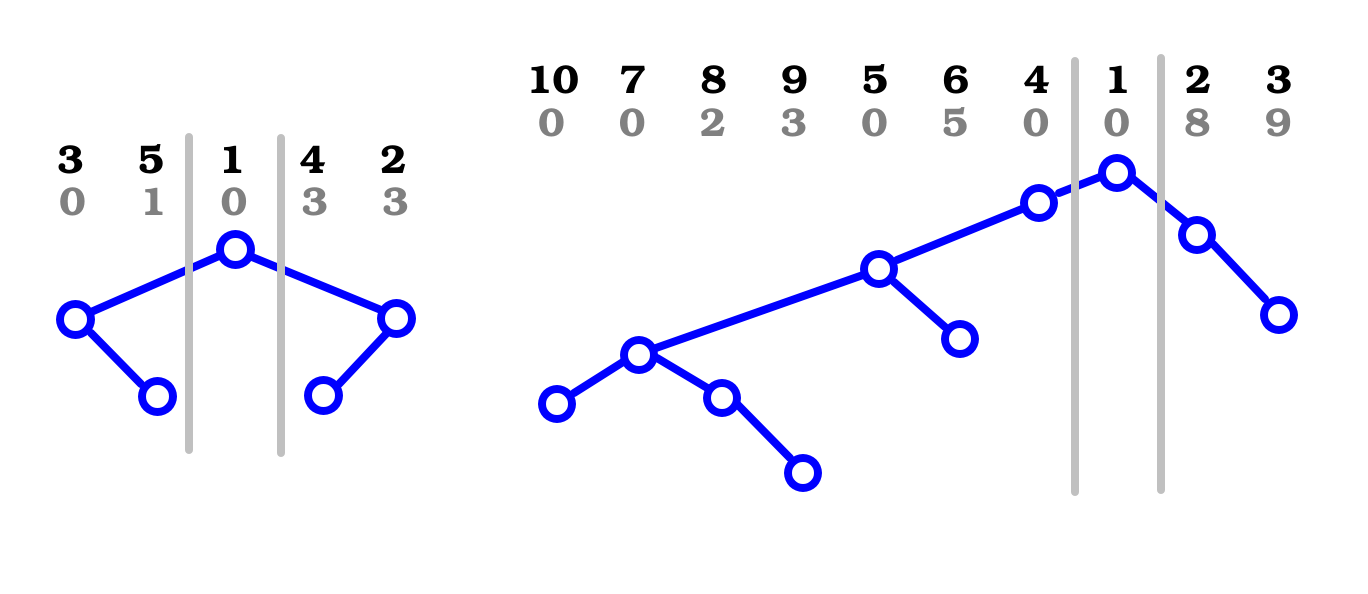
我们要求排列的方案数。你发现,每一个排列其实相当于在做这样一件事情:填充这个树的结点。并且按照排列中1-N的顺序填充时,总能够保证,一个结点在被填充时其父节点已被填充。换言之,排列方案数等价于树上填充的方案数。
关于排列方案数还有一种理解。把这棵树当作一个DAG,从父节点向子节点连两条有向边构成的DAG。显然根节点是唯一入度为0的点。那么排列方案数等价于这个DAG的拓扑序方案数。
于是我们来求这个所谓的拓扑方案数。考虑一个类似树形DP的过程。f[u]表示以u为根的子树的拓扑方案数。显然这个子树拓扑序的第一个元素是u,而对于u的左右子节点(u_l,u_r),可以看作是把两个拓扑序列合并的过程。于是
merge(a,b)表示把两个长度分别为a,b的序列合并的方案数。size表示子树大小。
接下来考虑merge怎么做。容易想到递归的思路。合并(A[1sim a],B[1sim b]),可以把A的第一个元素插入到(B[i])的前面,或者(B[b])的后面。然后将剩下的a-1个元素与b-i+1个元素(或者0个元素)合并。
打表,就发现这是个组合数
于是做完。答案就是(f[root])。时间复杂度(O(nlog_2P)),其中(log_2P)是求逆元的复杂度
代码当时写了一个,懒得重写了。反正这玩意儿可做就对了(不超过60line)
一道DP题
顺便说一下T1吧
T1推一个DP出来是这样的
于是你发现这玩意儿并不能斜率emmm
可以线段树套凸包