1、伯努利实验
- 伯努利试验是只有两种可能结果的单次随机试验
- 进行一次伯努利试验，成功（X=1）概率为 p(0<=p<=1)，失败（X=0）概率为 1-p
- 在一次伯努利实验中，随机变量 X 服从伯努利分布（0-1分布）
- 如果试 E 是一个伯努利试验，将 E 独立重复地进行 n 次，则称这一串重复的独立试验为 n 重伯努利试验
2、（0-1）分布 / 伯努利分布
- 设随机变量 X 只能取 0 和 1 两个值，其分布律是：
- 如上分布，称 X 服从以 p 为参数的（0-1）分布、两点分布、伯努利分布
3、二项分布
- 二项分布 (Binomial distribution) 是 n 重伯努利试验成功次数的离散概率分布。
- 如果试验 E 是一个 n 重伯努利试验，每次伯努利试验的成功概率为 p，X 代表成功的次数，则 X 的分布律为
- 令 q=(1-p)，则 X 的分布律为
- 由于
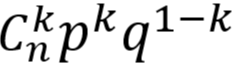刚好是二项式 
的展开式中出现 
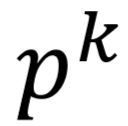的那一项，因此称随机变量 X 服从参数为 n,p 的二项分布，记为 X~B(n,p)
- 从定义可以看出，0-1/伯努利分布是二项分布在 n=1 时的特例
4、多项分布
- 多项式分布（Multinomial Distribution）是二项式分布的推广
- 二项式做 n 次伯努利实验，规定了每次试验的结果只有两种可能性
- 如果现在还是做 n 次试验，只不过每次试验的结果可以有 m 种，且 m 种结果互斥且发生的概率和为 1，则其中一个结果
发生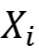 
次的概率就是多项式分布 - 多项式分布的分布律为：
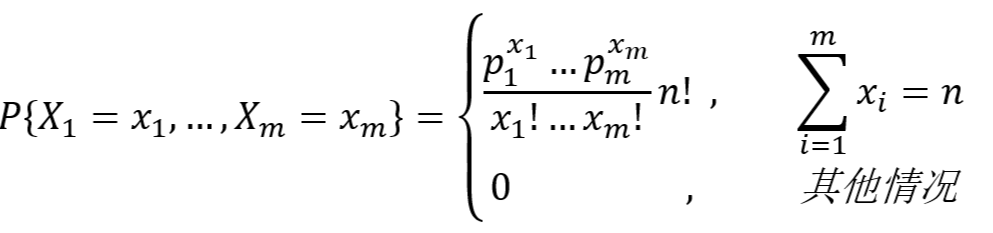
5、Beta分布
- 共轭分布(conjugacy)：后验概率分布函数与先验概率分布函数具有相同形式
- 在试验数据比较少的情况下，直接用最大似然法估计二项分布的参数可能会出现过拟合的现象（比如，扔硬币三次都是正面，那么最大似然法预测以后的所有抛硬币结果都是正面，该预测明显是不合理的）
- 为了避免这种情况的发生，可以考虑引入先验概率分布来控制参数，防止出现过拟合现象
- 对于上述这种可用二项分布表示。且需要引入先验概率的问题，一个最好的方法就是用 beta 分布，这表示在进行实验之前我们就有了该实验的一个先验分布，此后我们可用新的实验信息对先验的 beta 分布进行更新
- beta 分布与二项分布时共轭先验的，即其先验分布是 beta 分布，而后验分布同样是 beta分布
- 举例说明：
- 现在有一个棒球运动员，我们希望能够预测他在这一赛季中的棒球击球率是多少。
- 根据棒球的历史信息，我们知道这个击球率应该是0.215到0.36之间，均值在 0.27 左右
- 接下来我们将这些先验信息转换为 beta 分布的参数，我们可以取 α=81，β=219
- 之所以取这两个参数是因为：
- beta分布的均值是
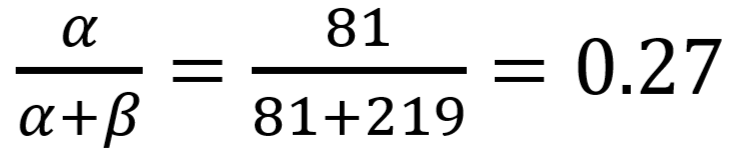
- 如上，我们假设了初始（先验）的 beta 分布为 Beta(α,β)=Beta(81,219)
- 假设该运动员在该赛季已经打了 n 次球，其中击中了 a 次，未击中有 b 次，a+b=n，则基于先验的 beta 分布以及新的数据，后验的 beta 分布为：Beta(α+a , β+b)=Beta(81+a , 219+b)
- beta分布的均值是
6、迪利克雷分布（Dirichlet distribution）
- 狄利克雷分布(Dirichlet distribution)是多项分布的共轭分布，也就是它与多项分布具有相同形式的分布函数。
- 狄利克雷分布即多元的 beta 分布，其原理和 beta 分布一致
7、泊松分布
- 设随机变量 X 所有可能取值为 0,1,2,…，而取各个值的概率为
- 如上，则称 X 服从参数为 λ 的泊松分布，记为 X~π(n,p)
- 设
，当 n→∞ 时，有如下性质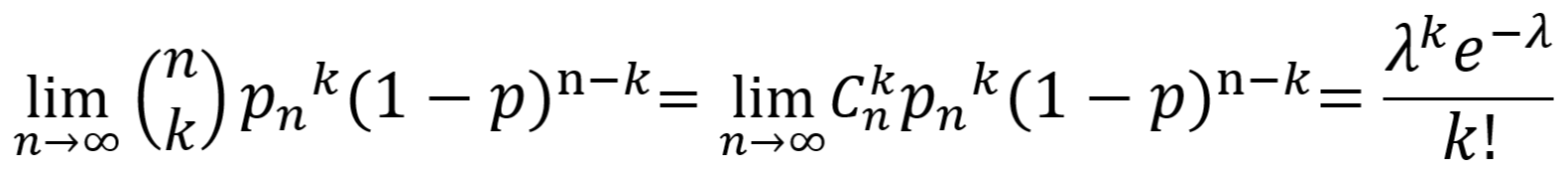
8、边缘概率/条件概率
- 假设有一个和两个变量相关的概率分布 p(x,y)
- 关于其中一个特定变量的边缘分布则为给定其他变量的条件概率分布：
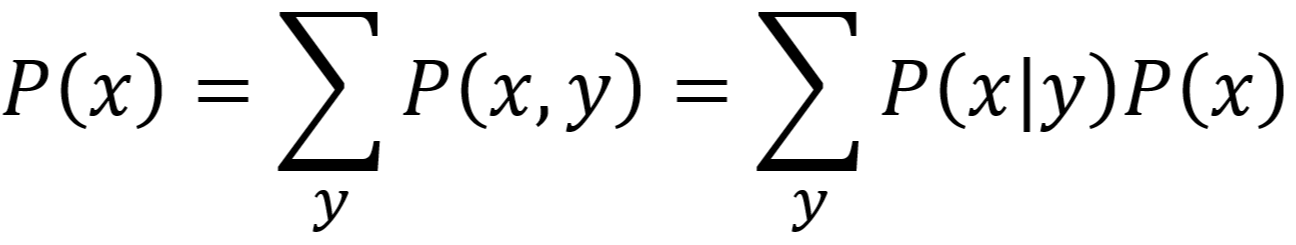
- 在这个边缘分布中，我们得到是关于一个变量的概率分布，而不再考虑另一变量的影响，实际上进行了降维操作。