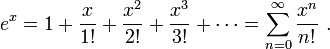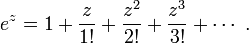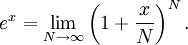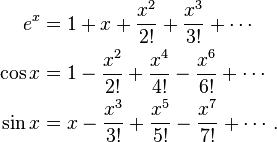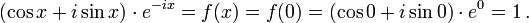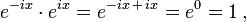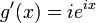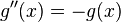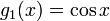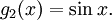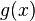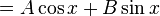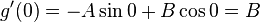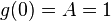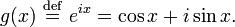http://en.wikipedia.org/wiki/Complex_number#Formal_development
In a rigorous setting, it is not acceptable to simply assume that there exists a number whose square is -1. The definition must therefore be a little less intuitive, building on the knowledge of real numbers. Write C for R2, the set of ordered pairs of real numbers, and define operations on complex numbers in C according to
- (a, b) + (c, d) = (a + c, b + d)
- (a, b)·(c, d) = (a·c − b·d, b·c + a·d)
Since (0, 1)·(0, 1) = (−1, 0), we have found i by constructing it, not postulating it. We can associate the numbers (a, 0) with the real numbers, and write i = (0, 1). It is then just a matter of notation to express (a, b) as a + ib.
--------------
http://en.wikipedia.org/wiki/Euler%27s_formula
Definitions of complex exponentiation
In general, raising e to a positive integer exponent has a simple interpretation in terms of repeated multiplication of e. Raising e to zero or a negative integer exponent can be understood as repeated division. A rational number exponent can be defined by radicals of e, and an irrational number exponent can be defined by finding rational-number exponents that are arbitrarily close to the irrational-number exponent, in a limit process. However, to define and understand a complex number exponent of e, a different type of generalization is required for the concept of exponentiation.
In fact, several definitions are possible. All of them can be proven to be well-defined and equivalent, although the proofs are not included in this article.
Taylor series definition
It is well-known that, for any real x, the following series is equal to ex:
(in other words, this is the Taylor series for the real exponential function, and it has an infinite radius of convergence). This invites the following definition of ez for complex z:
This can be proven to be well-defined; in particular, the series converges for any z.
Analytic continuation definition
A simple-to-state, equivalent definition is that ez, for complex z, is the analytic continuation of the function ex for real x. This can be proven to be well-defined; in particular, it yields a single-valued function on the complex plane.
Limit definition
It is well-known that, for any real x, the following limit is equal to ex:
This motivates the following definition of ez for complex z:
Differential equation definition
For real x, the function f(x)=ex is well-known to be the unique real function satisfying the differential equation:
for all x. This motivates a definition of f(z)=ez for complex z as the function that satisfies the differential equation:
for all complex z, where the derivative in f'(z) is defined in the sense of a complex derivative. This can be proven to yield a unique function which is well-defined everywhere on the complex plane.
Proofs
Various proofs of this formula are possible. The first proof below starts with the "Taylor series definition" of ez, while the other two use the "Differential equation definition" of ez (see above).
Using Taylor series
Here is a proof of Euler's formula using Taylor series expansions as well as basic facts about the powers of i:
and so on. The functions ex, cos x and sin x of the (real) variable x can be expressed using their Taylor expansions around zero:
For complex z we define each of these functions by the above series, replacing the real variable x with the complex variable z. This is possible because the radius of convergence of each series is infinite. We then find that
The rearrangement of terms is justified because each series is absolutely convergent. Taking z = x to be a real number gives the original identity as Euler discovered it.
Using calculus
Define the (possibly complex) function ƒ(x), of real variable x, as
The derivative of ƒ(x), according to the product rule, is:
Therefore, ƒ(x) must be a constant function in x. Because ƒ(0) is known, the constant that ƒ(x) equals for all real x is also known. Thus,
Multiplying both sides by eix and using
it follows that
Using ordinary differential equations
Define the function g(x) by
Considering that i is constant, the first and second derivatives of g(x) are
because i 2 = −1 by definition. From this the following 2nd-order linear ordinary differential equation is constructed:
or
Being a 2nd-order differential equation, there are two linearly independent solutions that satisfy it:
Both cos and sin are real functions in which the 2nd derivative is identical to the negative of that function. Any linear combination of solutions to a homogeneous differential equation is also a solution. Then, in general, the solution to the differential equation is
for any constants A and B. But not all values of these two constants satisfy the known initial conditions for g(x):

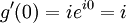 .
.
However these same initial conditions (applied to the general solution) are
resulting in
and, finally,